其实并没有统一的定义。

“数据结构是数据对象，以及存在于该对象的实例和组成实例的数据元素之间的各种联系。这些联系可以通过定义相关的函数来给出。” ==Sartaj Sahni《数据结构、算法与应用》

“数据结构是ADT(抽象数据类型Abstract Data Type)的物理实现。”==Clifford A.Shaffer《数据结构与算法分析》

“数据结构(data structure)是计算机中存储、组织数据的方式。通常情况下，精心选择的数据结构可以带来最优效率的算法。”==中文维基百科

然而，数据结构与算法是经常挨在一起的东西。

1.1.1关于数据组织-案例:图书摆放

先说个问题:

如果给了一堆数据、存储空间，那么如何存储这些数据？

这是一个不科学的问题。

当问一个数据怎么组织的时候，其实是跟这个数据的规模有关系的，难度是不同的。

如何在书架上摆放图书

然而，书如何摆放，是说如何做这个事情的。

关键操作在于插入和查找。

方法一:随便放

忘了到底有没有。从头到尾过一遍，才知道。

方法二:书名拼音字母顺序

每次都找跟中间的比较。大范围的中间、再中间...最后中间。

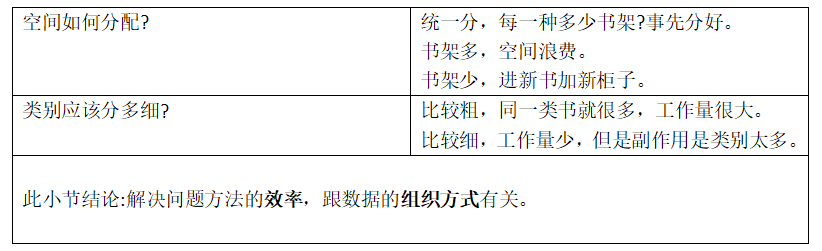
方法三:书架划分区域-摆放类别-书名拼音字母顺序

小总结(效率->数据组织方式)

1.1.2关于空间使用-案例:PrintN函数实现

循环实现

#include<stdio.h>
void PrintN(int N);
int main(void){
	int N;
	scanf("%d",&N);
	PrintN(N);
	return 0;
}
void PrintN(int N){
	if(N){
		int i;
		for(i=1;i<=N;i++){
			printf("%d\n",i);
		}
	}
	return;
}


D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>Prin
tN-Loop
D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>gcc
PrintN-Loop.c -o PrintN-Loop
...正常输出略
1111110
1111111

递归实现

#include<stdio.h>
void PrintN(int N);
int main(void){
	int N;
	scanf("%d",&N);
	PrintN(N);
	return 0;
}
void PrintN(int N){
	if(N){
		PrintN(N - 1);
		printf("%d\n",N);
	}
	return;
}


D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>gcc
PrintN-Recursion.c -o PrintN-Recursion
D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>Prin
tN-Recursion
1111
1
2
3
...正常输出略
1110
1111

D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>Prin
tN-Recursion
1111111
...直接终止

#跑多次看看效果。

#如果理解递归，那么写出的递归程序简洁、清楚，那么容易当别人和自己理解。但是，计算机并不愿意跑递归程序，递归程序对空间的占用有时很恐怖。

#那么这个递归程序发生了什么呢？ 它把能用的空间全部吃掉，但还不够用，就爆掉了。这是非正常的终止，还不来不及打任何一个数字，就非正常的终止跳出了 。

小总结(效率->空间利用率)

此小节结论:解决问题方法的 效率 ，跟空间的利用率有关。

1.1.3关于算法效率-案例:计算多项式值

有位叫秦九韶(南宋著名数学家，与李冶、杨辉、朱世杰并称宋元数学四大家。)的老祖宗，巧妙的用了结合律。

方法一

这个函数，实际上就是对这个标准定义式的一个很直接的翻译。

但是这个函数会被专业的程序猿所鄙视，这个函数肯定不能这么写。

#include<stdio.h>
#include<math.h>
#define N 5
double f1(int n,double a[],double x);
int main(void){

	double a[N] = {1,2,3,4,5};
	double x = 2;

	double result = f1(N,a,x);

	printf("result = %f\n",result);

	return 0;
}
double f1(int n,double a[],double x){
	int i;
	double p = a[0];
	for(i = 1;i <= n;i++){
		p += (a[i] * pow(x,i));
	}
	return p;
}

D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>gcc
duoxiangshi1.c -o duoxiangshi1

D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>duox
iangshi1
result = 129.000000

方法二(提出公因子)

这样一直一层一层的往里面把X当成一个公因子提出来。

这样，程序是从里向外计算的。

这是实现这个函数的标准程序。

#include<stdio.h>
#include<math.h>
#define N 5
double f2(int n,double a[],double x);
int main(void){

	double a[N] = {1,2,3,4,5};
	double x = 2;

	double result = f2(N,a,x);

	printf("result = %f\n",result);

	return 0;
}
double f2(int n,double a[],double x){
	int i;
	double p = a[n];
	for(i = n;i > 0;i--){
		p = a[i - 1] + x * p;
	}
	return p;
}


D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>gcc
duoxiangshi2.c -o duoxiangshi2

D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>duox
iangshi2
result = 129.000000

时间测试:clock()

然而，上述第二个函数就一定比第一个函数实现的好而快吗？

函数clock():捕捉从程序开始运行到clock()被调用时所耗费的时间。这个时间单位是clock tick，即”时钟打点”。

tick是系统的相对时间单位,也称为系统的时基,来源于定时器的周期性中断。

常数CLK_TCK(或CLOCKS_PER_SEC):机器时钟每秒所走的时钟打点数。

案例:函数clock()

#include<stdio.h>
#include<time.h>
/*
clock_t是clock()函数返回的变量类型。
*/
clock_t start,stop;
/*
记录被测函数运行时间,以秒为单位。
*/
double duration;
void MyFunction();
/*
tick是系统的相对时间单位,也称为系统的时基,来源于定时器的周期性中断。
*/
int main(void){

	/*
	不在测试范围内的准备工作写在clock()调用之前
	*/
	/*
	开始计时,start中存的是从main函数开始运行,一直到start被赋值这个时刻。
	它们一共走了多少ticks。
	*/
	start = clock();
	/*
	被测函数
	*/
	MyFunction();
	/*
	停止计时
	从main函数开始执行,一直到这次clock被调用的时候,一共走了多少ticks。
	*/
	stop = clock();
	//计算运行时间
	duration = ((double)(stop - start))/CLK_TCK;
	/*
	其他不在测试范围的处理写在后面,例如输出duration的值。
	*/
	return 0;
}
void MyFunction(){
}

案例:函数clock()与具体多项式(综合计算)

#九阶多项式有十个系数，还有一个常数，所以下标是从0开始计算的，那么第i个系数等于i就好了。

方法一

#include<stdio.h>
#include<time.h>
#include<math.h>

clock_t start,stop;
double duration;
//多项式最大项数,即多项式阶数+1
#define MAXN 10

double f1(int n,double a[],double x);
double f2(int n,double a[],double x);

int main(void){

	int i;
	//存储多项式的系数
	double a[MAXN];
	for(i = 0;i < MAXN;i++){
		a[i] = (double)i;
	}

	printf("1=======================================\n");

	start = clock();
	f1(MAXN - 1,a,1.1);
	stop = clock();
	duration = ((double)(stop - start))/CLK_TCK;
	printf("ticks1 = %f\n", (double)(stop - start));
	printf("duration1 = %6.2e\n", duration);

	printf("2=======================================\n");

	start = clock();
	f2(MAXN - 1,a,1.1);
	stop = clock();
	duration = ((double)(stop - start))/CLK_TCK;
	printf("ticks2 = %f\n", (double)(stop -start));
	printf("duration2 = %6.2e\n", duration);

	printf("3=======================================\n");

	return 0;
}
double f1(int n,double a[],double x){

	int i;
	double p = a[0];
	for(i = 1;i <= n;i++){
		p += (a[i] * pow(x,i));
	}
	return p;

}
double f2(int n,double a[],double x){

	int i;
	double p = a[n];
	for(i = n;i >= 1;i--){
		p = a[i - 1] + x * p;
	}
	return p;

}


D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>gcc clockfunc2.c -o clockfunc2

D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>clockfunc2
1=======================================
ticks1 = 0.000000
duration1 = 0.00e+000
2=======================================
ticks2 = 0.000000
duration2 = 0.00e+000
3=======================================

可以发现这一段代码中，居然两个阶段的代码一模一样，挺傻的一个程序。

而结果，居然都是0。因为程序跑得太快了，运行时间都不到一个tick，所以这个clock函数根据就捕捉不到这俩函数的时间区别。

那么这些函数的运行时间，如何测试这里不到1个tick呢？

这里可以让被测函数重复运行充分多次，使得测出的总的时钟打点间隔充分长，那么计算被测函数平均每次运行的时间即可 !

把时间积累出来，如果觉得一万次不够多，那么百万次、千万次、上亿次，一直跑到这个间隔的时间能够被这个clock函数捕捉到，最后计算它单次时间的时候，只要把总的时间除以重复的次数即可!

看方法二 。

方法二(优化)

#继方法一的优化。

#include<stdio.h>
#include<time.h>
#include<math.h>

clock_t start,stop;
//记录被测函数总运行时间,以秒为单位。
double duration1;
//记录被测函数单次运行时间,以秒为单位。
double duration2;
//多项式最大项数,即多项式阶数+1
//被测函数最大重复调用次数
#define MAXN 10000

double f1(int n,double a[],double x);
double f2(int n,double a[],double x);

int main(void){

	int i;
	//存储多项式的系数
	double a[MAXN];
	for(i = 0;i < MAXN;i++){
		a[i] = (double)i;
	}

	printf("1=======================================\n");

	start = clock();
	//重复调用函数以获得充分多的时钟打点数
	for(i = 0; i<MAXN;i++){
		f1(MAXN - 1,a,1.1);
	}
	stop = clock();
	duration1 = ((double)(stop - start))/CLK_TCK;
	printf("ticks1 = %f\n", (double)(stop - start));
	printf("duration1 = %6.2e\n", duration1);
	duration2 = duration1/MAXN;
	printf("duration2 = %6.2e\n", duration2);
	printf("2=======================================\n");

	start = clock();
	//重复调用函数以获得充分多的时钟打点数
	for(i = 0; i<MAXN;i++){
		f2(MAXN - 1,a,1.1);
	}
	stop = clock();
	duration1 = ((double)(stop - start))/CLK_TCK;
	printf("ticks2 = %f\n", (double)(stop -start));
	printf("duration1 = %6.2e\n", duration1);
	duration2 = duration1/MAXN;
	printf("duration2 = %6.2e\n", duration2);
	printf("3=======================================\n");

	return 0;
}

double f1(int n,double a[],double x){
	int i;
	double p = a[0];
	for(i = 1;i <= n;i++){
		p += (a[i] * pow(x,i));
	}
	return p;
}

double f2(int n,double a[],double x){
	int i;
	double p = a[n];
	for(i = n;i >= 1;i--){
		p = a[i - 1] + p * x;
	}
	return p;
}

#这两组数据的相对大小，应该都是差了一个数量级这个样子。

D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>gcc clockfunc3.c -o clockfunc3

D:\doc\C\c-primer-plus\workspace\C-Primer-Plus-Project01\data-structures-and-algorithms\MOOC-ZhejiangUniversity\1.1>clockfunc3
1=======================================
ticks1 = 19031.000000
duration1 = 1.90e+001
duration2 = 1.90e-003
2=======================================
ticks2 = 5812.000000
duration1 = 5.81e+000
duration2 = 5.81e-004
3=======================================

小总结(效率->算法巧妙程度)

此小节结论:解决问题方法的 效率 ，跟算法的巧妙程度有关。

1.1.4抽象数据类型

到底什么是数据结构

三个关键对象:

组织方式=>说的是上一节的如何放书的问题。

操作关联=>表明数据对象并不是孤立的。

算法=>操作数据对象与对其操作的方法。

逻辑结构

==线性结构:

比如，我们如果一开始就把这个书架想象成一个简单的一层架子，书是一个挨着一个放的，那么除了一头一尾两本书外，每一本书的前面只有一本书，后面只有一本书，如果给每一本书编号的话，那么这种是一对一的结构，管这种结构叫做”线性结构”。

==树:

另外一种组织方式:先把图书分类，那么这一个类别的编号里面，对应着许多本书，这是一个一对多的逻辑结构，这种结构叫做”树”。

==图:

假设我们还统计这样一些信息，这一本书都有哪些人买过，买了这本书的人还买过其他什么书，于是呢，其实就是一本书对应着许多人，而一个人又对应了许多本书，这是一个多对多的、很复杂的关系网，那么这个关系网对应的就是一个”图”的结构。

物理结构

除了逻辑结构以外，我们还有数据对象在 计算机里面的物理存储结构 ，也就是我们说的这些逻辑结构在机器的内存里面要怎么一个放法，是连续存放呢，还是东一个西一个隔开放呢？也就是说，是用一个数组来存储它呢？还是用一个链表来存储它呢？这个就是属于物理存储结构。

抽象数据类型

描述数据结构，一个很好的办法就是”抽象.数据类型”。

两个关键词:抽象(但不具体)、数据类型。

无关:机器、物理结构、算法和编程语言。

数据对象集:强调描述此数据对象 是什么东西 ？并不关心” 如何做 ”。

数据集合相关联的操作集:这里不能单纯的去讲如何去处理图书，而是要对这些图书进行操作的，这两件事情:图书的摆放与跟它的操作是紧密结合在一起的。

在开发语言角度来说，“这两件事情”在C语言中是单独处理的。但是在一些面向对象的语言中，比如C++、java，它们很好的为这个数据类型专门设计了这样的”类”的机制，把数据集和其操作集封装在一个类里面，是抽象的但不具体的。

案例: ” 矩阵 ” 的抽象数据类型定义

为什么这个就叫做”抽象”的表示呢？

“抽象”在哪里呢？

首先，在描述数据对象集的时候，说a是矩阵元素的值，这个值是float、double还是int类型？我们在这个描述类型描述中间是不关心的。这是自定义的类型，是一个通用的element type(元素类型)，你需要什么，就把它define定义成什么，是跟矩阵中的元素到底是什么类型是没有关系的，避免了重写代码与替换数据类型的问题。

然后，只说了这是个M*N的矩阵，但并没有说用哪种存储结构去存储此矩阵对象，比如二维数组、一维数组、十字链表？那么在抽象数据类型定义的时候，都是不关心其是如何实现的。

再次，在求矩阵加法的时候，并没有说是先按行加还是先按列加。

最后，实现的语言也统统不用管。

那么，这就是所谓的抽象。

本节总结