这是一个求”从Ai到Aj连续的一段子列的和”的函数。

对N个整数来说，有很多这样的连续的子列。

这里要求的是，所有连续子列和里面最大的那个。

如果这个和是负数的话，那么我们最后返回0作为结束。

一个最直接、最暴力的办法就是:把所有的连续子列和全部都算出来，然后从中找到最大的那一个。

算法1:O(N^3)

//输入整数序列:int A[]
//输入整数序列里面元素的个数:int N
int maxSubSeqSum1(int A[],int N){

	int ThisSum,MaxSum = 0;
	int i,j,k;
	//i是子列左端位置
	for(i = 0;i < N;i++){
		//j是子列右端位置
		for(j = i;j < N;j++){
			//ThisSum是从A[i]到A[j]的子列和
			ThisSum = 0;
			for(k = i;k <= j;k++){
				ThisSum += A[k];
			}
			//如果刚得到的这个子列和更大,则更新结果.
			if(ThisSum > MaxSum){
				MaxSum = ThisSum;
			}
		}//j循环结束
	}//i循环结束

	return MaxSum;

}

总的来说，有两重for循环。

最外面的这层for循环i对应的是子列左端的位置，是从A[i]开始。

然后里面的for循环j对应的是子列和右边的位置，一直到A[j]开始。

所以j总是大于等于i的，从i开始计数。

在这个双重for循环里面，我们开始暴力的去求这个子列和，

所以我们还需要做一重for循环k，k从i一直加到j。

=分割线=

现在考虑一下，这个算法的复杂度是多少？T(N)=O(N^3)。

很直观的理由就是，这里有三层嵌套的for循环。

虽然说，如果每一层都是从0到N的，那么很显然，三个乘在一起就是N立方，但是这里没那么明显。

因为这里只有第一重for循环是从0到N的，后面的for循环一个是从i到N的，一个是从i到j的.

但是，无论如何，用一下我们中学的证明技巧，仍然可以证明，整个的运算量是N立方乘以一个常数。

T(N)=O(N^3)

其实可以说，这个算法真的还挺笨的，N立方也是一个很恐怖的函数了，比如N等于10W、100W、1000W。

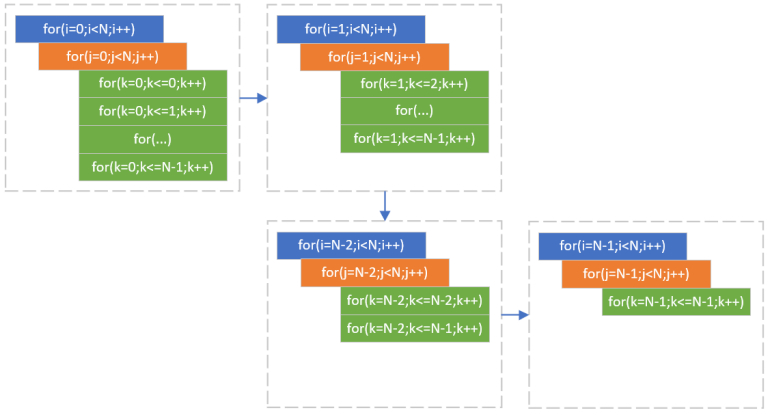
它到底不聪明在哪儿呢？

主要在于最里层的k循环。

当i=0时，最后一个k循环是从0一直加到N-1。

当i=1时，最后一个k循环是从1一直加到N-1。

等等。

中间有一个很大的问题，

当我们知道当前从i到j的”结果部分和”的时候，要计算下一个j的时候，根本没必要从头开始往后加，所以当j增加了1的时候，其实只要在前面那个i到j的”结果部分和”后面加1个元素就好了，这个k循环完全是多余的。

算法2:O(N^2)

//输入整数序列:int A[]
//输入整数序列里面元素的个数:int N
int maxSubSeqSum2(int A[],int N){

	int ThisSum,MaxSum = 0;
	int i,j;
	//i是子列左端位置
	for(i = 0;i < N;i++){
		//ThisSum是从A[i]到A[j]的子列和
		ThisSum = 0;
		//j是子列右端位置
		for(j = i;j < N;j++){
			//对于相同的i,不同的j,只要在j-1次循环的基础上累加1项即可.
			ThisSum += A[j];
			//如果刚得到的这个子列和更大,则更新结果.
			if(ThisSum > MaxSum){
				MaxSum = ThisSum;
			}
		}//j循环结束
	}//i循环结束

	return MaxSum;

}

这里，在外面仍然有一个i循环，i是子列的左端位置。

当j每增加一个值的时候，只是在当前这个部分和的基础上，加一个A[j]就可以了。

很显然，有两套for循环的嵌套，所以这里的时间复杂度是O(N^2)。

所以说，这个算法已经比前面的O(N^3)要聪明许多了，但是呢，它还不是最好的。

一个专业的程序猿，设计了一个算法，当发现这个算法是O(N^X)的时候，应该下意识地、本能地就应该想想，有没有可能把它改进成NlogN呢？那还能快很多呢。

算法3:分而治之O(NlogN)

大概的思路就是把一个比较大的复杂的问题切分成小的块，然后分头去解决它们，最后再把结果合并起来，这就是”分而治之”。

那么这个思想在解决这个问题的时候，是如何分工的呢？

首先，假设我们的问题是放在这么一个数组里面的。

这个算法的第一步是”分”，也就是把这个数组从中间一分为二，然后递归的去解决左右两边的问题。

递归的去解决左边的问题，那么会得到左边的一个最大子列和。

递归的去解决右边的问题，那么会得到右边的一个最大子列和。

那么，现在不能说这两个数中间最大的一个就一定是结论了。

还有一种情况就是跨越边界的最大子列和。

把这个三个结果都找到了以后，那么我们最后的结果一定是这三个数中间最大的那一个。

所以这个叫做”分”，

最后的合成就叫做”治”，

总起来说叫做”分而治之”。

=分割线=

案例:

8个数字，第一步，从中间一分为二，先递归的解决左半边，在递归的进入左半边的时候，继续把它一分为二，继续的递归到左半边，继续把它一分为二。

注:以下计算，先求最大子列和，再求跨越边界最大子列和。

个人理解:最大子列和为一个或某2N连续值的计算得到的值，而跨越边界最大子列和把前后相邻的”最大子列和”再次相加，每次少了1/2的重复计算量。

最后得到了O(NlogN)的时间复杂度。

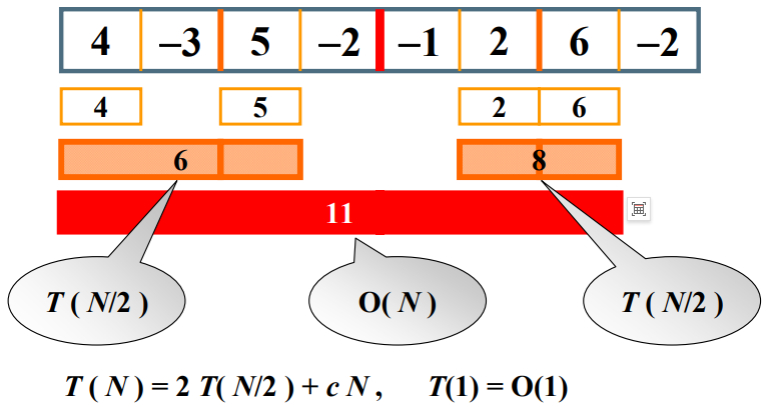
先看左边的4和-3(从4和-3中间画条线):

分的时候，从这个左边我们会得到最大子列和，是4。而右边是负数-3，返回0(如果序列中所有整数皆为负数，则输出0。再比如，最后一个是负数了，就不用在执行加操作了)。

那么，跨越这个边界的最大和也是4。

再看右边的5和-2(从5和-2中间画条线):

最大子列和与跨越边界的最大和都是5。

红线右边的数字计算同理。

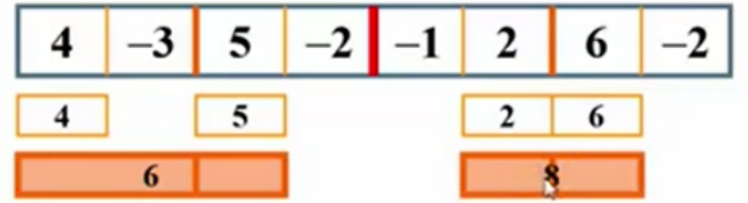
再次算跨越边界的最大和。

从-3与5中间画条线:

从线往左边扫描两个格:得-3，然后(-3+4)=1，最大子列和为1。

从线往右边扫描两个格:得5，然后(5-2)=3，最大子列和为5。

所以跨越边界的这个最大子列和(1+5)=6，即红色线左边四个数的递归函数返回值为6。

从2与6中间画条线:

从线往左边扫描两个格:得2，然后(2-1)=1，最大子列和为2。

从线往右边扫描两个格:得6，然后(6-2)=4，最大子列和为6。

所以跨越边界的这个最大子列和(2+6)=8，即红色线右边四个数的递归函数返回值为8。

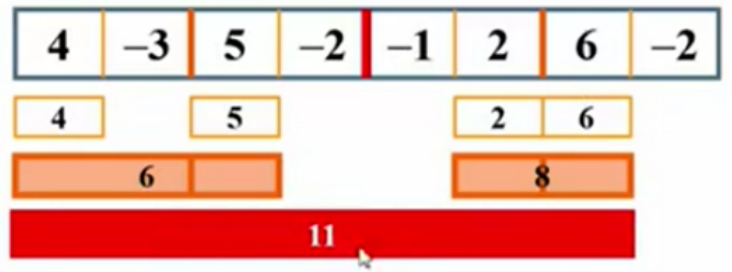
再次算跨越边界的最大和。

从-2与1中间画条线:

从线往左边扫描四个格:(-2)+5+(-3)+4=4

从线往右边扫描四个格:(-1)+2+6=7(最后一个格再减值就不是最大值了，就没意义了)

所以跨越边界的这个最大子列和(4+7)=11。

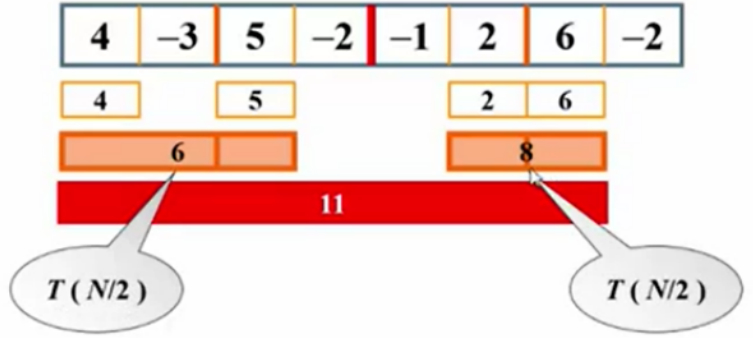
这里的难点在于，如何分析此算法的时间复杂度？

当解决的这个问题中有N个数字的时候，如果时间复杂度为T(N)，那么得到的这半边数字的时间复杂度为T(N/2)，因为规模减半了。

而这里是如何得到中间这个跨越边界最大子列和的呢？

做法就是:从中间开始，往左边扫描，然后往右边扫描， 每个元素都被扫描了一次(扫描的每个元素的时间) ，所以，得到这个结果的复杂度应该是N的一个常数倍。

由此，就得到了关于T(N)的一个递归公式，

T(N)是由”算出左边的复杂度”加上”算出右边的复杂度”，再加上”跨越中间的复杂度”，这三个部分组成的，也就是两倍的T(N/2)加上一个N的常数倍(当N=1时为常数)。

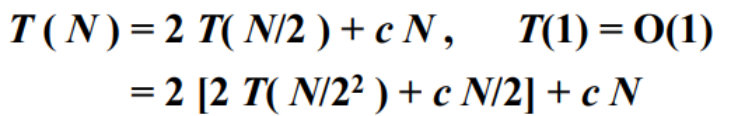
这里如何递推呢？

可以把这个N换成N/2，然后代到代码中去。

T(N/2)按照公式递推地展开成2T(NB/4)加上N/2的常数倍。

跟原来的cN加在一起，得到一个2倍的cN。

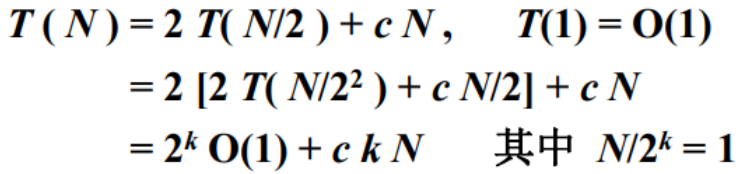
如果觉得上述规律不够清楚的话，可以进一步展开，直到T里面的这个数等于1为止。

过了K步以后，一共乘以K个2，中间项变成1，所以变成常数O(1)。

每展开一层就多了一个cN，所以展开K步以后就是ckN。

那么K和N是什么关系呢？

N/2除了K次以后，最终会得到1(理想情况)。

两边乘以2的K次方，这一项是得到N的，2的K次方就是1(T和常数c同理)。

什么是K呢？

K就是log以2为底N的对数:log2N。

所以在分析复杂度的时候，我们就有了两项:O(N)与O(NlogN)。

那么，当两个复杂度在一起的时候，取得是比较大的那一项，所以，就得到了这整个算法的复杂度为O(NlogN)。

算法3:源码-分而治之O(NlogN)

//分而治之O(NlogN)
//输入整数序列:int A[]
//输入整数序列里面元素的个数:int N
int maxSubSeqSum3(int A[],int N){
	return DivideAndConquer3(A, 0, N - 1);
}
//分治法求List[left]到List[right]的最大子列和。此方法被递归调用。
int DivideAndConquer3(int List[],int left,int right){
	//存放左右子问题的解
	int MaxLeftSum, MaxRightSum;
	//存放跨越分界线的结果
	int MaxLeftBorderSum, MaxRightBorderSum;
	int LeftBorderSum, RightBorderSum;
	int center,i;

	//递归的终止条件,子列只有1个数字。
	if(left == right){
		if(List[left] > 0){
			return List[left];
		}else{
			return 0;
		}
	}

	//下面是分的过程
	center = (left + right)/2;//找到中分点
	//递归求得两边子列的最大和
	MaxLeftSum = DivideAndConquer3(List, left, center);
	MaxRightSum = DivideAndConquer3(List, center + 1, right);

	//求跨越分界线的最大子列和
	//开始从中间向左边扫描
	MaxLeftBorderSum = 0;
	LeftBorderSum = 0;
	for(i = center; i >= left;i--){
		LeftBorderSum += List[i];
		if(LeftBorderSum > MaxLeftBorderSum){
			MaxLeftBorderSum = LeftBorderSum;
		}
	}
	//结束从中间向左边扫描
	//开始从中间向右边扫描
	MaxRightBorderSum = 0;
	RightBorderSum = 0;
	for(i = center + 1;i <= right;i++){
		RightBorderSum += List[i];;
		if(RightBorderSum > MaxRightBorderSum){
			MaxRightBorderSum = RightBorderSum;
		}
	}
	//结束从中间向右边扫描


	//返回"治"的结果/返回3个整数中的最大值
	return Max3(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum);

}
//返回"治"的结果/返回3个整数中的最大值
int Max3(int A, int B, int C){
	return A > B ? A > C ? A : C : B > C ? B : C;
}

算法4:在线处理O(N)

//输入整数序列:int A[]
//输入整数序列里面元素的个数:int N
int maxSubSeqSum4(int A[],int N){

	int ThisSum,MaxSum = 0;
	int i;
	for(i = 0; i < N;i++){
		//向右累加
		ThisSum += A[i];
		if(ThisSum > MaxSum){
			//发现更大和则更新当前结果.
			MaxSum = ThisSum;
		}else if(ThisSum < 0){
			//如果当前子列和为负,则不可能使后面的部分和增大,抛弃之.
			ThisSum = 0;
		}
	}

	return MaxSum;
}

这个算法的复杂度是O(N)，是线性的。

其中for循环以及里面的if-else都是常数数量级的复杂度。

这个必须是可能得到的最快的一个算法了。

因为无论如何都需要把每个元素都过一遍，当读入的时候也需要O(N)的时间，所以，解决整个问题居然可以用O(N)的速度，这已经是可以想象的、最快、最好的算法了。

当然，一个算法效率如此的高，一般来说是有副作用的，正确性不是那么的明显，也就是说，别人要理解这个程序是怎么工作的，略微有点困难。

=分割线=

再结合案例 :

(

为什么这个算法叫”在线处理”呢？

“ 在线 ”的意思是指每输入一个数据就进行 即时处理 ，在任何一个地方中止输入，算法都能正确给出当前的解。

)

第一件事:把当前子列和把当前的这个数加进来。

-1加进来，-1并不能使当前的最大和变大，所以这块就被跳过去了。

如果当前的子列和是负的，那么就直接把它抛弃掉，把当前子列和重新归零。

为什么可以这么做呢？因为我们是要求连续的子列和，所以如果当前子列和到这里，下一步我们是要顺着往后去求和的。

如果现在求和是负数的话，往后面不管加什么数，它都只能让后面的数越变越小，不可能越变越大，所以呢，还不如从头开始。

发现3比MaxSum要大，所以当前的最大子列和记为3。

发现加上-2后的总体值是+1，总有可能让后面的和变得更大，所以继续加。

发现4比MaxSum要大，所以当前的最大子列和记为1+4=5。

对于前四个数字而言，这个结果是对的。

这个就叫做”在线处理”。

发现加上-6后的总体值是负数-1，那么直接把它抛弃掉。

重新归零，开始考虑下一个。

这里继续1+6=7。

到最后的-1，输入就结束了，那么最终结果就是7。

所以这个算法为什么快呢？ 一旦发现当前的子列和是负数的话，它其实就没有用了，直接就把抛弃掉，扫描后面的就可以 。

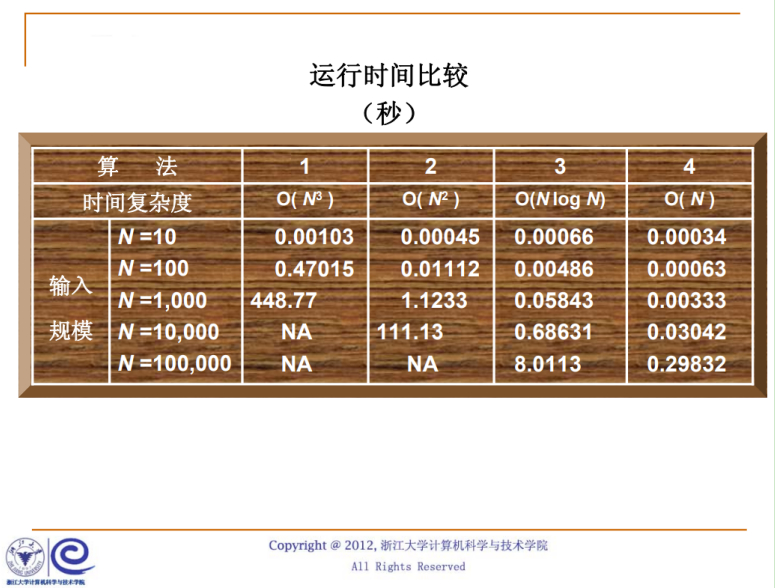
这种表是在某一台机器跑出来的结果。

可以把这个算法都实现一下。

N^3的这个算法跑到N=10000的时候就已经跑不动了。

NA的意思是Not Available，就是不算了。

当然这个结果里面，并没有算输入和输出的时间。

算法源码汇总

#include<stdio.h>
//O(N^3)
int maxSubSeqSum1(int A[],int N);
//O(N^2)
int maxSubSeqSum2(int A[],int N);
//分而治之O(NlogN)
int maxSubSeqSum3(int A[],int N);
int DivideAndConquer3(int A[],int left,int right);
int Max3(int A, int B, int C);
//在线治理O(N)
int maxSubSeqSum4(int A[],int N);
//程序入口
int main(void){
	return 0;
}

//O(N^3)
//输入整数序列:int A[]
//输入整数序列里面元素的个数:int N
int maxSubSeqSum1(int A[],int N){

	int ThisSum,MaxSum = 0;
	int i,j,k;
	//i是子列左端位置
	for(i = 0;i < N;i++){
		//j是子列右端位置
		for(j = i;j < N;j++){
			//ThisSum是从A[i]到A[j]的子列和
			ThisSum = 0;
			for(k = i;k <= j;k++){
				ThisSum += A[k];
			}
			//如果刚得到的这个子列和更大,则更新结果.
			if(ThisSum > MaxSum){
				MaxSum = ThisSum;
			}
		}//j循环结束
	}//i循环结束

	return MaxSum;

}

//O(N^2)
//输入整数序列:int A[]
//输入整数序列里面元素的个数:int N
int maxSubSeqSum2(int A[],int N){

	int ThisSum,MaxSum = 0;
	int i,j;
	//i是子列左端位置
	for(i = 0;i < N;i++){
		//ThisSum是从A[i]到A[j]的子列和
		ThisSum = 0;
		//j是子列右端位置
		for(j = i;j < N;j++){
			//对于相同的i,不同的j,只要在j-1次循环的基础上累加1项即可.
			ThisSum += A[j];
			//如果刚得到的这个子列和更大,则更新结果.
			if(ThisSum > MaxSum){
				MaxSum = ThisSum;
			}
		}//j循环结束
	}//i循环结束

	return MaxSum;

}

//在线治理O(N)
//输入整数序列:int A[]
//输入整数序列里面元素的个数:int N
int maxSubSeqSum4(int A[],int N){

	int ThisSum,MaxSum = 0;
	int i;
	for(i = 0; i < N;i++){
		//向右累加
		ThisSum += A[i];
		if(ThisSum > MaxSum){
			//发现更大和则更新当前结果.
			MaxSum = ThisSum;
		}else if(ThisSum < 0){
			//如果当前子列和为负,则不可能使后面的部分和增大,抛弃之.
			ThisSum = 0;
		}
	}

	return MaxSum;
}

//分而治之O(NlogN)
//输入整数序列:int A[]
//输入整数序列里面元素的个数:int N
int maxSubSeqSum3(int A[],int N){
	return DivideAndConquer3(A, 0, N - 1);
}
//分治法求List[left]到List[right]的最大子列和。此方法被递归调用。
int DivideAndConquer3(int List[],int left,int right){
	//存放左右子问题的解
	int MaxLeftSum, MaxRightSum;
	//存放跨越分界线的结果
	int MaxLeftBorderSum, MaxRightBorderSum;
	int LeftBorderSum, RightBorderSum;
	int center,i;

	//递归的终止条件,子列只有1个数字。
	if(left == right){
		if(List[left] > 0){
			return List[left];
		}else{
			return 0;
		}
	}

	//下面是分的过程
	center = (left + right)/2;//找到中分点
	//递归求得两边子列的最大和
	MaxLeftSum = DivideAndConquer3(List, left, center);
	MaxRightSum = DivideAndConquer3(List, center + 1, right);

	//求跨越分界线的最大子列和
	//开始从中间向左边扫描
	MaxLeftBorderSum = 0;
	LeftBorderSum = 0;
	for(i = center; i >= left;i--){
		LeftBorderSum += List[i];
		if(LeftBorderSum > MaxLeftBorderSum){
			MaxLeftBorderSum = LeftBorderSum;
		}
	}
	//结束从中间向左边扫描
	//开始从中间向右边扫描
	MaxRightBorderSum = 0;
	RightBorderSum = 0;
	for(i = center + 1;i <= right;i++){
		RightBorderSum += List[i];;
		if(RightBorderSum > MaxRightBorderSum){
			MaxRightBorderSum = RightBorderSum;
		}
	}
	//结束从中间向右边扫描


	//返回"治"的结果/返回3个整数中的最大值
	return Max3(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum);

}
//返回"治"的结果/返回3个整数中的最大值
int Max3(int A, int B, int C){
	return A > B ? A > C ? A : C : B > C ? B : C;
}