堆栈在计算机中有广泛用途，比如函数调用、递归、表达式求值。

这里说的表达式是算术表达式。

如果表达式没有优先级，那么求解很容易。

但是计算机中的表达式中的运算符是有优先级的，所以问题就变得复杂了。

这里看到的中缀表达式和后缀表达式是等价的。

后缀表达式的求值相对容易，因为在碰到符号的时候，运算数在前面已经知道了，不像中缀表达式一样还要等着去后面看。

案例(按计算机一般处理数据的方法，一个个扫描，一个个处理):

推测“a+b*c的前缀表达式

步骤:{

“b*c为*bc”

“a+*bc为+a*bc”

}

推测“a+b*c-d/e的前缀表达式

步骤:{

“d/e为/de”

“b*c为*bc”

“a+*bc-/de为-+a*bc/de”(注意这里后面的减号-要放在加号+的前面)

}

当碰到运算数时:把最近的两个数做对应的运算，那么需要一种数据结构做有效地组织，特点是先放进去的后拿出来，后拿进去的先拿出来做运算，这实际就是堆栈。

堆栈一定有一个特点:逐个的往里面放，反过来往外拿。

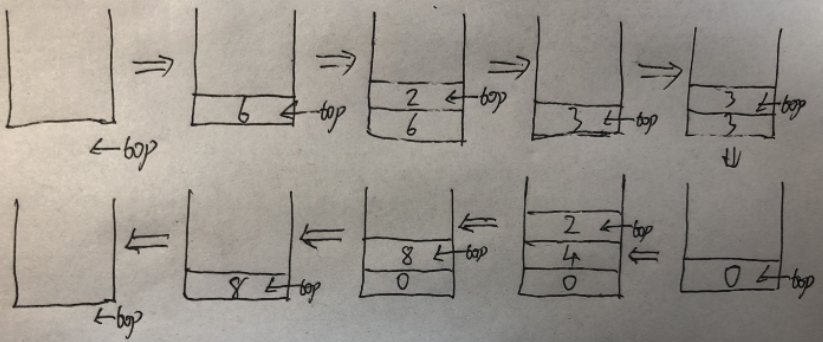
案例推测:“62/3-42*+=?”的后缀表达式的值(看下述堆栈的描述)
步骤:
{
“62/为6/2=3”
“33-为3-3=0”
“42*为4*2=8”
“08+=为0+8=8”
}

T(N)=O(N)其时间复杂性是线性的 。

这里最主要的操作是插入和删除，插入要判断是否满，删除要判断是否空。

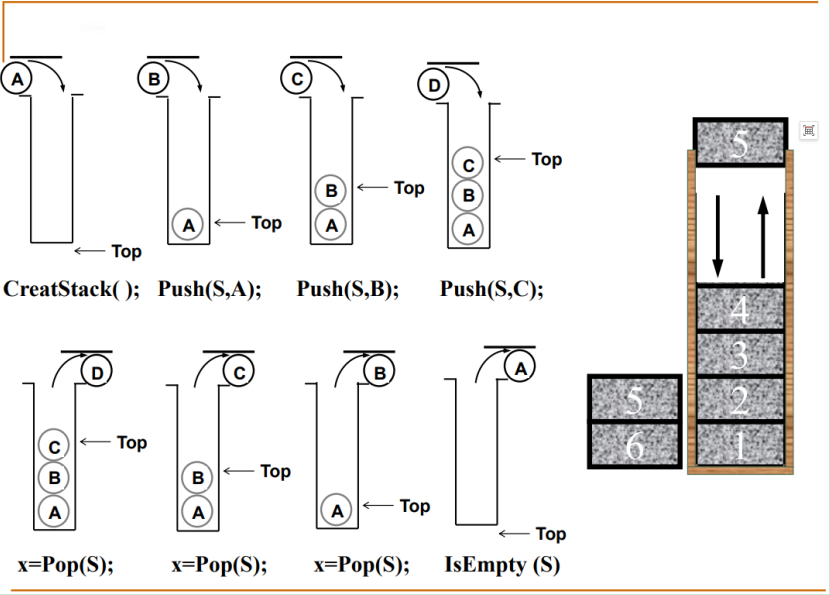
此形象图形产生的结果就是把原来进行的顺序倒个个。

不能。如果是ABCD，那么像上述(2)中的样式穿插交替进行，那么就会有更多种可能。

{

“push:ABCD”

“pop:DCBA”

}

{

“push:ABCD”

“pop:CBAD”

}

{

“push:ABCD”

“pop:CBAD”

}

{

“push:ABCD”

“pop:ACBD”

}

{

“push:ABCD”

“pop:BACD”

}

{

“push:ABCD”

“pop:BADC”

}