把运算数放到堆栈中去，碰到运算符号的时候，把运算数抛出来做计算，再放到堆栈里面去，整个过程就是从左到右读入表达式的各项，然后根据运算数跟运算符号分别做不同的处理。

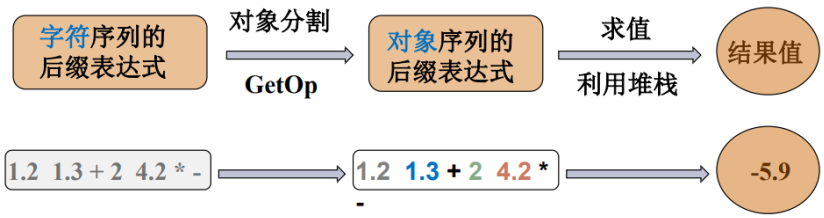
(1.2 1.3 + 2 4.2 * -) -----> (1.2 + 1.3 - 2 * 4.2 = -5.9)

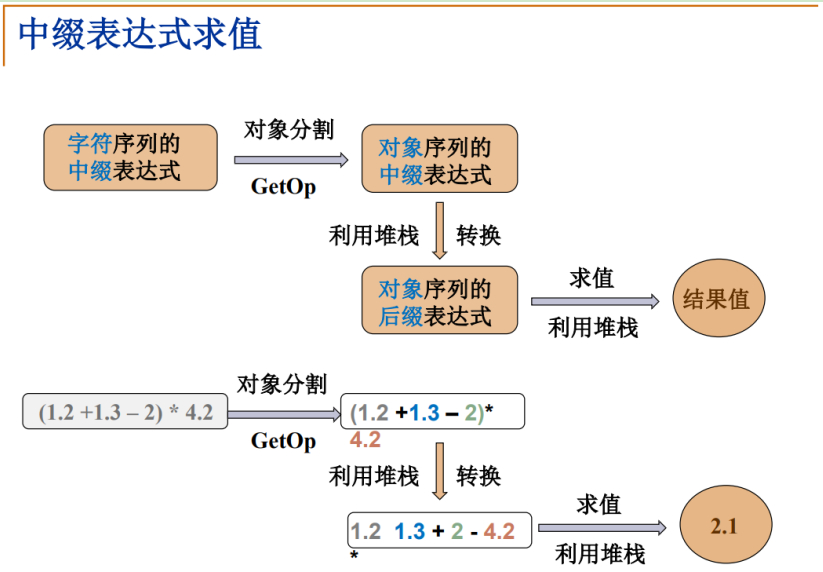
中缀表达式转后缀表达式(无括号)

案例描述:

碰到加号，那加号是否能输出，暂时未知，要看后面运算符号的优先级。

所以先把运算符号+先记下来。

碰到9输出。

碰到除号，能不能输出？除号的优先级比加号要高，但是这个时候能否把9除以3呢？

不一定，后面如果还有一个优先级，比如说指数运算3的5次方，那此时这个除号还不能做除法运算，所以当看到除号的时候，仍需要先记下来。

再下面的符号是3，那么3输出。

减号的优先级要比除号低，那么这个时候，除号可以出来了。

所以这样一种处理过程，碰到运算数就把它输出，碰到运算符号就等着，看后面的运算符号到底怎么样。

如果前面的一个运算符号的优先级比我要来的高，就说明它可以拿来计算，如果它的优先级比我低，那么这个时候当前的运算符号还不能说可以直接拿来运算，因为后面可能还有优先级比我高的，所以仍然要保留起来。

所以，在这个过程中，就需要一种结构来实现运算符号的存储，这里就是堆栈结构！

堆栈结构的特点就是:按顺序来保留这个运算符号，当要做比较的时候呢，就跟前面的一个去比较。

中缀表达式转后缀表达式(有括号)

案例:

中缀表达式为a * (b + c)/d = ?

后缀表达式为abc+*d/

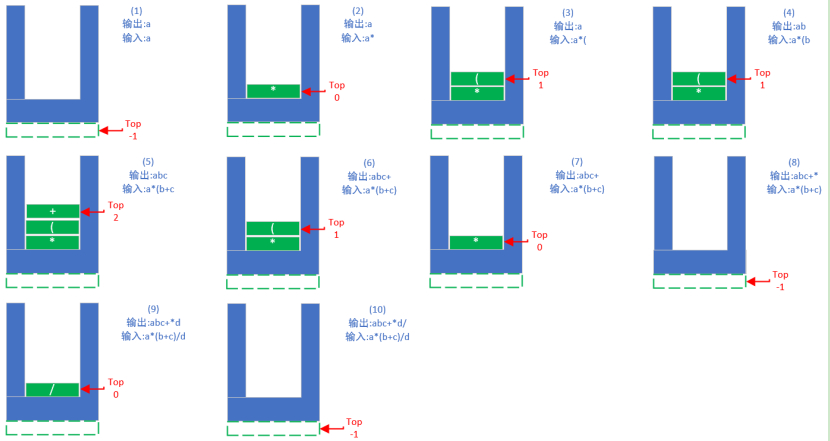
策略:

碰到运算数，就输出，碰到运算符号，就存起来和后面的运算符号做个比较。

同一个优先级的时候，顺序是从左到右。比如除号和乘号，乘号先运算的话，那么乘号就可以从堆栈中出来了。

T(N)=O(N)

从这个过程中可以看到，它的时间复杂度是线性的，每循环一次处理一个运算数或运算符号。

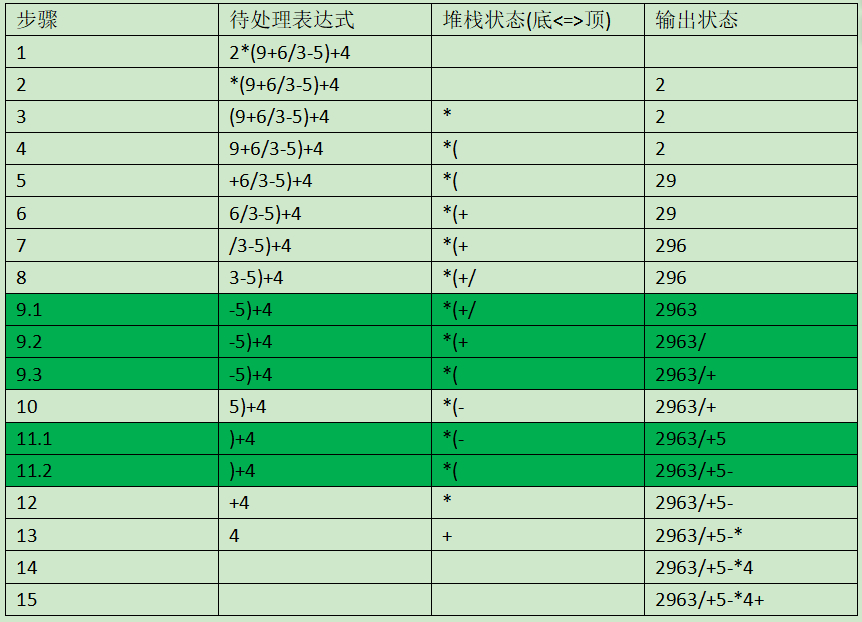
中缀表达式转后缀表达式示例

原案例:

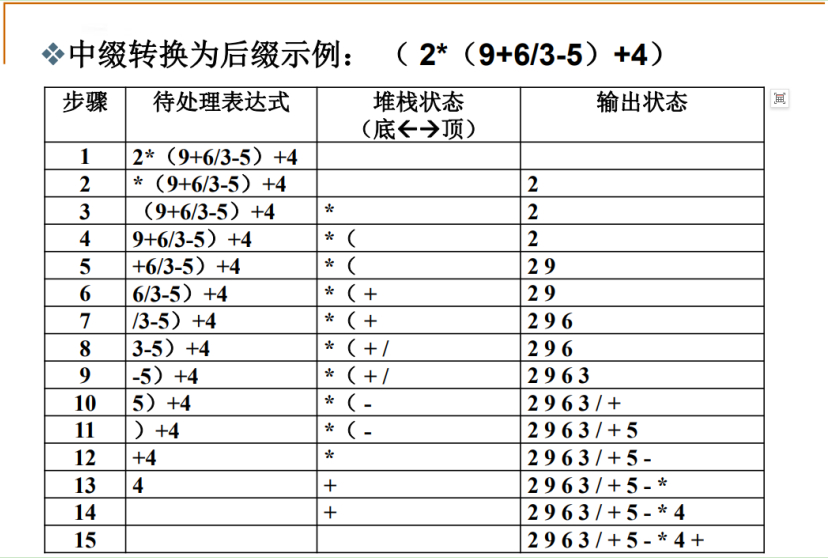
自己推算(细节优化):

其他应用

在程序设计语言中，从一个函数调用另外一个函数，等函数执行完了之后再回过来头，这里需要解决一个问题，调用完了回到哪里？回来的时候原来的状态能恢复出来，那么需要把调用之前的一些变量的状态以及调用回来之后准备要执行的程序的地址保存起来。

(一是)从一个函数调用另一个函数的时候，还可能再调用下一个函数，下一个函数可能还会再调用下一个函数，如果是这种一系列函数的调用过程，就需要保存一系列的东西，而函数调用回来的时候，是倒过来一步步地返回，所以需要一个管理的机制，能把之前调用的一些变量状态以及准备要返回的地址保留起来，而这个过程可能是一系列执行的，所以需要一系列的恢复过来，这样一种能够保存这些变量跟返回地址的这种数据结构的组织方式，必须有一种特点，按照顺序地存，然后按倒过来的顺序返回，这个特点其实就是堆栈，更重要的是，它实现了一种递归函数调用的一种实现机制，如果没有堆栈这种一种实现机制，递归函数要实现是非常困难的。

(二是)回溯算法是递归函数一种主要思想，叫老鼠走迷宫。

老鼠要从一个入口进去找到一条路径，从一个口出。在整个过程当中，只能不断地试探，当到某一步各种可能性试探都走不通的时候，它要回到上一步的位置，然后在上一步的位置继续试探，要把试探路径都保存起来，等到哪一步试探不成功的时候，要回到最近的一次试探状态。

(三是)图里面的深度优先搜索的实现。