2.3.1 队列及顺序存储实现

堆栈跟队列一样，也是一种受限制的线性表，比如日常排队。

队列最重要的两个操作:入队和出队。

而一般的线性表可以在任何位置进行插入和删除。

5将队头元素从队列中删除并返回。一定是位于队列的头。

#include<stdio.h>
#define MaxSize<储存数据元素的最大个数>
//队列结构
struct QNode{
	//一维数组
	ElementType Data[MaxSize];
	//记录队列头元素位置的变量
	int front;
	//记录队列尾元素位置的变量
	int rear;
};
typedef struct QNode *Queue;

数组工作队列

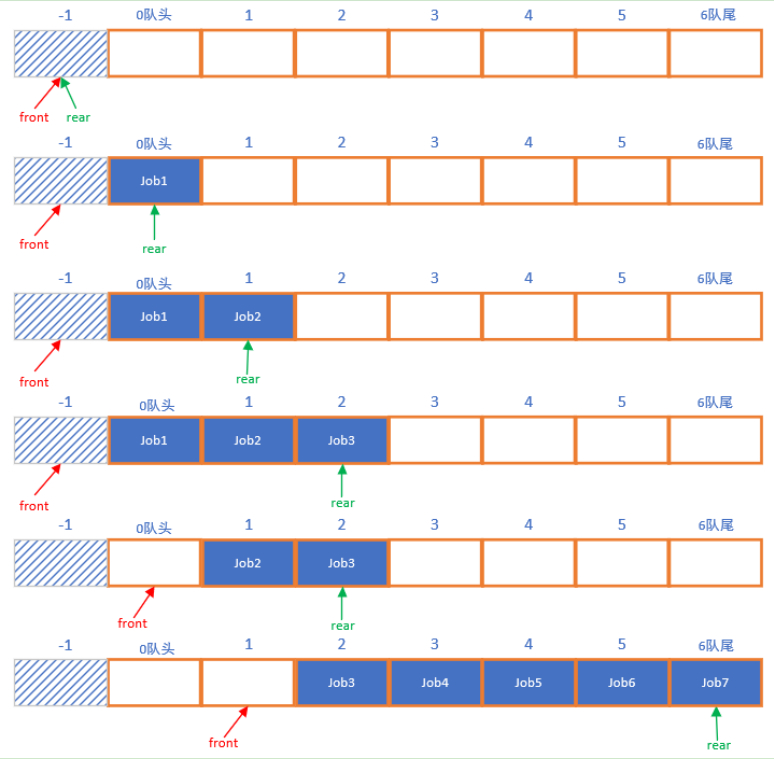
当front和rear都指向-1的时候，队列就是空的。

加入一个job，那么rear往右移动一位，rear+1。

删除一个job，那么front往右移动一位,front+1。

此时，如果还想再加入一个元素，那么就加不进去了，已经排到数组的最后了，实际上队列的前头还有空位，后面加不进去，加到前面就好了。

接下来，如果来新元素的时候，那么这就形成了顺环队列。

顺环队列

把数组掰过来形成一个环。

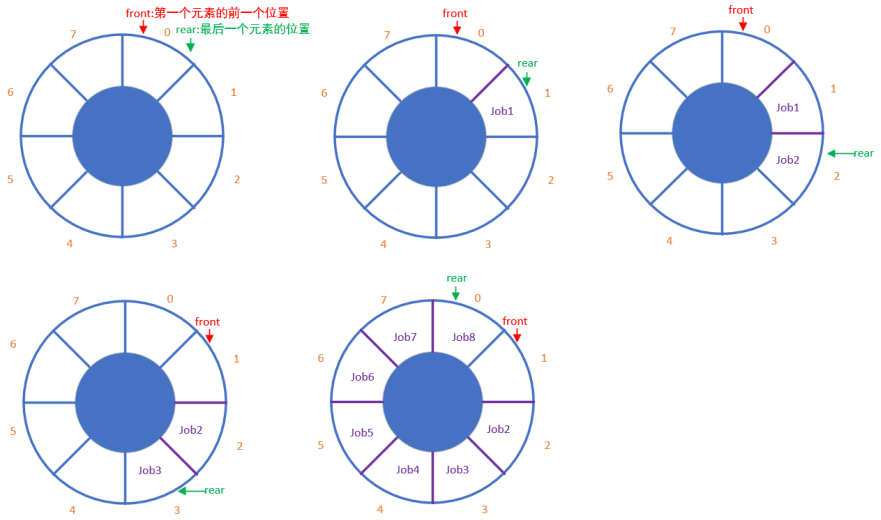
在此图中，当front和rear相等时候，队列是空的。

初始化时，front指向第一个元素的前一个位置，rear指向最后一个元素的位置。

加入一个job，那么rear往右移动一位，rear+1。

删除一个job，那么front往右移动一位,front+1。

把元素一直从0这个位置开始放，放满了，接下来再回过头来再放到0。

====问题:

现在已经放了7个元素了，如果这个时候再放进去一个元素，会产生:rear=front，按照这样的组织方式，如果rear=front，那么代表队列是空的，此时rear=front=1，队列满了，所以，

(问题一):当rear=front时，队列是满还是空呢？即:堆栈空和满的判别条件是什么呢？

(问题二):为什么会出现空、满无法区分？根本原因是什么呢？

我们判别队列的状态:空、一个元素、多个元素还是满，是根据front和rear的相对关系/它们的距离来判别的，front和rear的取值范围是0到n-1，在此例子中是0到7，所以此队列的状态是有9种情况:

0(空队列)

1(1个元素)

2(2个元素)

3(3个元素)

4(4个元素)

5(5个元素)

6(6个元素)

7(7个元素)

8(满队列)

可知，数组大小如果等于n的话，那么队列装载元素的情况有n+1种。

此时，如果用n来区分实际上存在的n+1种情况，是矛盾的，就像使用一个bit的0或1来表示3种情况是不合适的，这是此问题的根本原因。

====解决方案:

(方案1):使用额外标记size。

size用来记录当前队列元素的个数，当加入一个元素的时候，size+1，删除一个元素的时候，size-1，所以只要根据size是等于0还是等于n，就可以知道是空的还是满的。

(方案2):使用额外标记tag。(个人不推荐，即只用在插入时判断。复杂度也太高了。)

tag表示0和1，当插入一个元素的时候tag=1，当删除一个元素的时候tag=0，那么判断队列空或满，看tag就代表了最后一次操作是插入还是删除。

(方案3):仅使用n-1个数组空间。

到了n-1这个状态就认为是满了，此时，也不会出现front=rear时，不知道空或满的的情况，判断方式是通过求余函数，(小于n的值+1)对n求余，就能判断是front=rear=0还是front+1=rear的情况了。

/*
顺环队列
*/
/*
顺环队列:插入
*/
void addQueue(Queue PtrQ, ElmentType item){
	/*
	front和rear只指针的移动采用"加1取余"办法,
	体现了顺序存储的"循环使用"。
	*/
	if((PtrQ->rear + 1) % MaxSize == PtrQ->front){
		printf("队列满");
		return;
	}
	/*
	front和rear只指针的移动采用"加1取余"办法,
	体现了顺序存储的"循环使用"。
	*/
	PtrQ->rear = (PtrQ->rear + 1) % MaxSize;
	PtrQ->Data[PtrQ->rear] = item;
}
/*
顺环队列:删除
*/
ElementType deleteQueue(Queue PtrQ){
	if(PtrQ->front == PtrQ->rear){
		printf("队列空");
		return ERROR;
	}else{
		/*
		front和rear只指针的移动采用"加1取余"办法,
		体现了顺序存储的"循环使用"。
		*/
		PtrQ->front = (PtrQ->front+1) % MaxSize;
	}
	return PtrQ->Data[PtrQ->front];
}

2.3.2 队列的链式存储实现

单向链表，链头可做插入和删除操作，而链尾只能做插入操作。

/*
结点对象
*/
struct Node{
	ElementType Data;
	struct Node *Next;
};
/*
链队列结构
*/
struct QNode{
	/*
	指向队头结点
	*/
	struct Node *rear;
	/*
	指向队尾结点
	*/
	struct Node *front;
};
typedef struct QNode *Queue;
Queue PtrQ;

/*
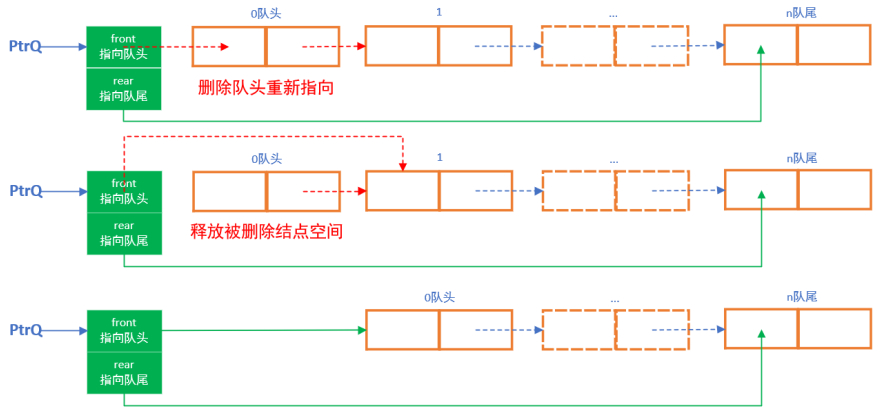
不带头结点的链式队列出队操作的示例。
反过来,也能推出来入队操作。
*/
ElementType DeleteQueue(Queue PtrQ){
	struct Node *FrontCell;
	ElementType FrontElem;
	if(PtrQ->front == NULL){
		printf("队列空");
		return ERROR;
	}
	/*
	存储即将被删除头结点的临时对象
	*/
	FrontCell = PtrQ->front;
	/*
	若队列只有一个元素
	*/
	if(PtrQ->front == PtrQ->rear){
		/*
		删除后队列置为空
		*/
		PtrQ->front = PtrQ->rear = NULL;
	}else{
		/*
		如果队列中不止一个元素,那么把头结点front删除之后,尾结点rear是不变的。
		*/
		PtrQ->front = PtrQ->front->Next;
	}
	FrontElem = FrontCell->Data;
	/*
	释放被删除结点空间
	*/
	free(FrontCell);
	return FrontElem;
}

C语言代码 : 队列的定义与操作-顺序存储

#include<stdio.h>
/*
队列的定义与操作-顺序存储
*/
int main(void){
	return 0;
}
typedef int Position;
struct QNode{
	/*
	存储元素的数组
	*/
	ElementType *Data;
	/*
	队列的头尾指针
	*/
	Position Front,Rear;
	/*
	队列最大容量
	*/
	int MaxSize;

}
typedef struct QNode *Queue;
Queue createQueue(int MaxSize){
	Queue Q = (Queue)malloc(sizeof(struct QNode));
	Q->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
	Q->Front = Q->Rear = 0;
	Q->MaxSize = MaxSize;
	return Q;
}
bool isFull(Queue Q){
	return ((Q->Rear + 1)%Q->MaxSize == Q->Front);
}
bool addQueue(Queue Q,ElementType X){
	if(isFull(Q)){
		printf("队列满");
		return false;
	}else{
		Q->Rear = (Q->Rear + 1)%Q->MaxSize;
		Q->Data[Q->Rear] = X;
		return true;
	}
}
bool isEmpty(Queue Q){
	return (Q->Front == Q->Rear);
}
ElementType deleteQueue(Queue Q){
	if(isEmpty(Q)){
		printf("队列空");
		return ERROR;
	}else{
		Q->Front = (Q->Front + 1)%Q->MaxSize;
		return Q->Data[Q->Front];
	}
}

C语言代码 : 队列的定义与操作-链式存储

#include<stdio.h>
/*
队列的定义与操作-顺序存储
*/
int main(void){
	return 0;
}
typedef int Position;
struct QNode{
	/*
	存储元素的数组
	*/
	ElementType *Data;
	/*
	队列的头尾指针
	*/
	Position Front,Rear;
	/*
	队列最大容量
	*/
	int MaxSize;

}
typedef struct QNode *Queue;
Queue createQueue(int MaxSize){
	Queue Q = (Queue)malloc(sizeof(struct QNode));
	Q->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
	Q->Front = Q->Rear = 0;
	Q->MaxSize = MaxSize;
	return Q;
}
bool isFull(Queue Q){
	return ((Q->Rear + 1)%Q->MaxSize == Q->Front);
}
bool addQueue(Queue Q,ElementType X){
	if(isFull(Q)){
		printf("队列满");
		return false;
	}else{
		Q->Rear = (Q->Rear + 1)%Q->MaxSize;
		Q->Data[Q->Rear] = X;
		return true;
	}
}
bool isEmpty(Queue Q){
	return (Q->Front == Q->Rear);
}
ElementType deleteQueue(Queue Q){
	if(isEmpty(Q)){
		printf("队列空");
		return ERROR;
	}else{
		Q->Front = (Q->Front + 1)%Q->MaxSize;
		return Q->Data[Q->Front];
	}
}