File Transfer题目:给了一大堆计算机,按照要求给计算机连接网络,一边随时来查询,任何两台计算机之间是否可以联网/传输文件,是否已经属于同一个集合。
这是一道非常典型的集合并查集应用题。
“此文内容来源于=>中国大学MOOC=>数据结构(浙江大学:陈越、何钦铭)”
“https://www.icourse163.org/learn/ZJU-93001#/learn/content”
集合的简化表示

此例是否可以更加简单?
此集合用数组来表达,数组类型是一个结构体,data是集合类型,parent相当于指针,检查父结点,如是根结点,那么下标为-1。
浪费时间的FOR循环:
如果要知道某个集合元素X属于的集合,data=X,在数组中查询是一个线性的过程,最坏的情况,数组中有N个元素,查数组中的最后一个元素,find函数反反复复找N遍,时间复杂度为O(N的平方)。
定义的data是一个整数,是否真的有必要专门一个数据阈去存储吗?
任何有限集合都可以被一一映射为0到N-1,计算机是从1开始编号,那么可以把1映射成0,以此类推,只要某个集合中的元素是有限个,就可以映射每一个元素。
这个问题就可以简化,把集合里的每个元素映射成数组的下标( 元素值就是下标 )去代表,那么数据阈data就可以去掉。
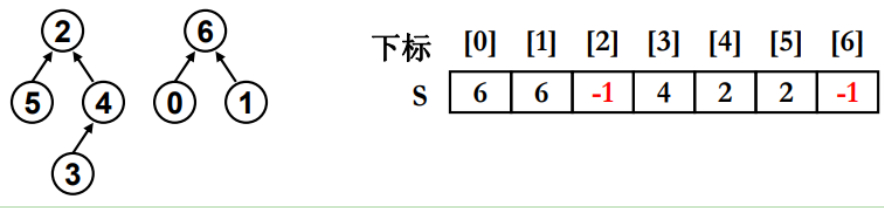
这里定义一个数组来表示一个集合。这里两个集合可以用这一个整型数组来存储。
集合里的每个元素值就是数组下标,S[元素值]就是每个元素的父结点元素值。
此数组中的集合数量可以根据-1的个数来衡量。
S[0]元素的父结点是元素6。
S[1]元素的父结点是元素6。
S[2]元素的父结点是没有的,默认根结点,父结点默认值-1。
S[3]元素的父结点是元素4。
S[4]元素的父结点是元素2。
S[5]元素的父结点是元素2。
S[6]元素的父结点是没有的,默认根结点,父结点默认值-1。
/*
集合的简化表示
*/
/*集合元素可以用非负整数表示,从0到N-1来表示,根结点的下标是一个整型.*/
typedef int ElementType;
/*默认用根结点的下标作为集合名称*/
typedef int SetName;
/*SetType是集合的类型,集合类型定义为整型数组.*/
typedef ElementType SetType[MaxSize];
/*
原data设置成整型ElementType
经过上述简化,当查找一个元素X,不用再去扫描整个数组,
而X这个元素直接就是数组的下标,S[X]就是每个元素对应的父结点元素值.
*/
SetName Find(SetType S, ElementType X){
/*默认集合元素全部初始化为-1*/
/*
如果父结点是大于等于0的,那么继续往上找.
如果找到-1,那说明上面没有父结点了,X就是这个根.
*/
for( ; S[X] >= 0; X = S[X]);
return X;
}
/*
这里保证Root1和Root2是不同集合的根结点.
这里省略了Root1和Root2是不同集合的根结点时才做合并操作,否则啥都不做直接返回.
这里就是把参数合法性的检查交给了用户去做.
*/
void Union(SetType S, SetName Root1, SetName Root2){
/*这里默认Root1和Root2是不同集合的根结点*/
S[Root2] = Root1;
}
题意理解与程序框架搭建
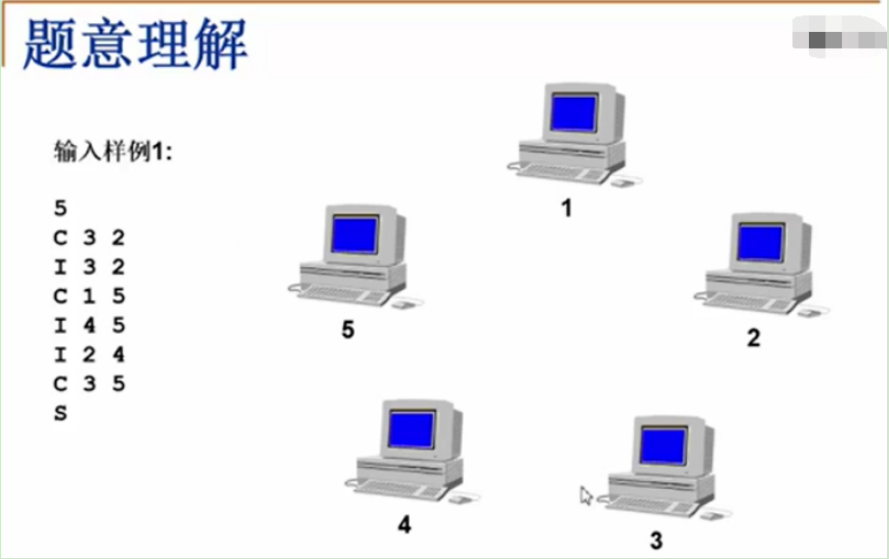
输入样例1:
第1行:5计算机的个数。
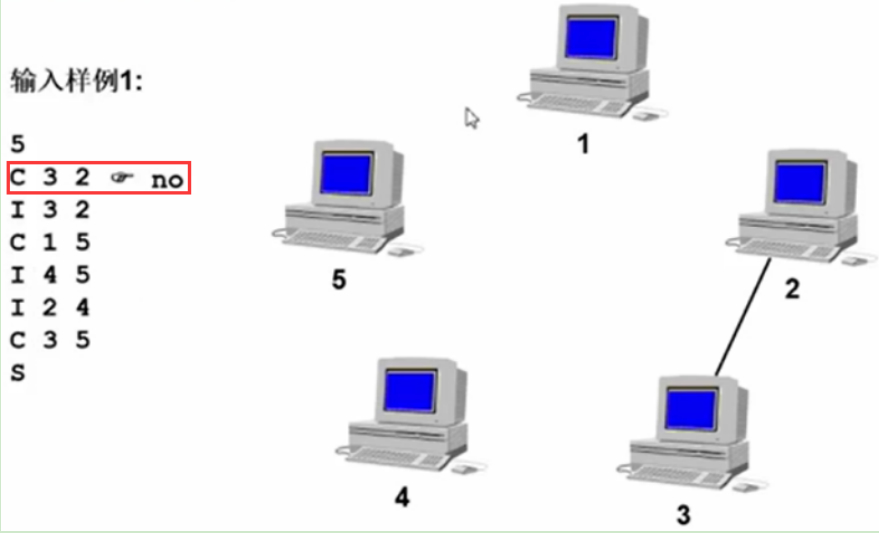
输入样例1:
第2行:字符C,表示check,查计算机3和计算机2之间是否连通,no。
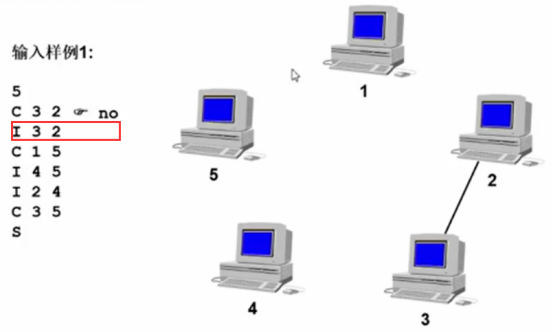
输入样例1:
第3行:字符I,表示input,查计算机3和计算机2之间加网线连通。
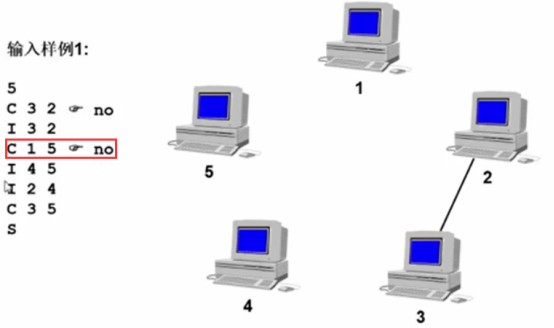
输入样例1:
第4行:字符C,表示check,查计算机1和计算机5之间是否连通,no。

输入样例1:
第5行:字符I,表示input,查计算机4和计算机5之间加网线连通。
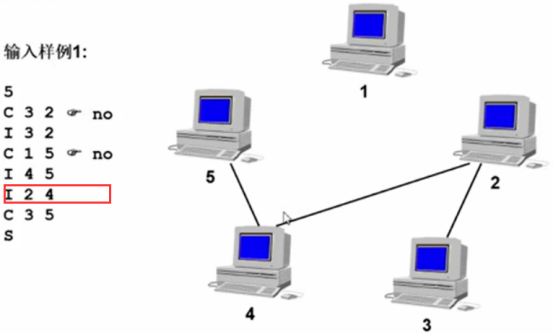
输入样例1:
第6行:字符I,表示input,查计算机2和计算机4之间加网线连通。

输入样例1:
第7行:字符C,表示check,查计算机3和计算机5之间是否连通,yes。
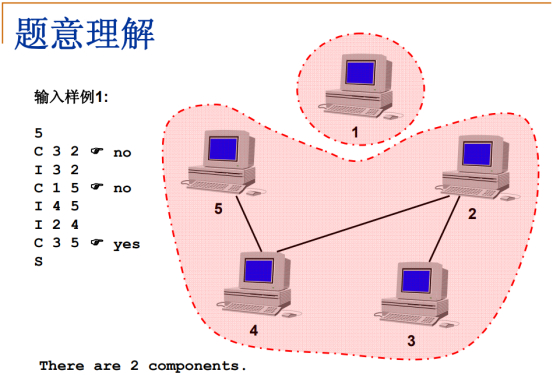
输入样例1:
第8行:S,输入结束。
对整个网络做判断,此集合中,任意两台计算机是直接或间接连通的,只有计算机1孤立,但是它自己也认为自己是连通的。
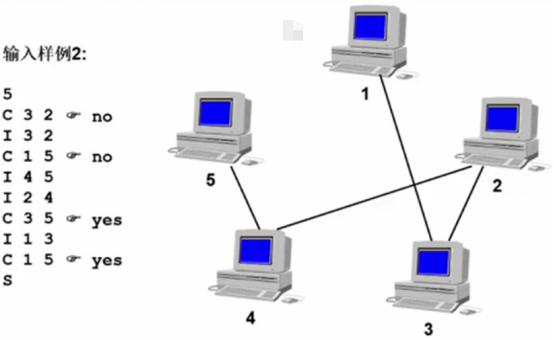
输入样例2:
各种执行方式同”输入样例1”。
此时,仅在计算机1和计算机3连接,那么计算机1和计算机5就是连通的了。
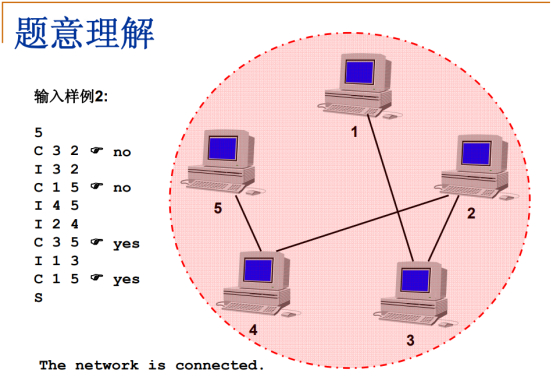
此时,计算机之间通过一个完全连通的网络相连接。
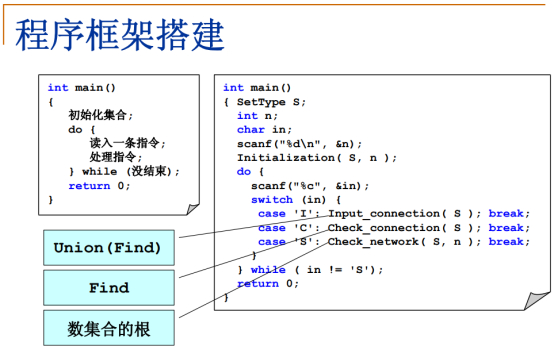
#include<stdio.h>
/*
集合并查集的简化
运行的关键取决于find函数与union函数.
*/
int main(void){
SetType S;
int n;
char in;
scanf("%d\n", &n);
/*
初始化集合
*/
Initialization(S, n);
do{
scanf("%c", &in);
switch(in){
case 'I':
/*
集合S初始化.
把两台计算机的编号读进来,检查两台计算机是否都连接成功(find),没连接好则连接(union).
*/
Input_connection(S);
break;
case 'C':
/*
读入待查询的计算机编号,是否在集合中(find).
*/
Check_connection(S);
break;
case 'S':
/*
整个网络是否连通.
数一下这个集合中有多少根结点,即:多少个联通的集合.
*/
Check_network(S, n);
break;
}
}while(in != 'S');
return 0;
}
void Input_connection(SetType S){
ElementType u, v;
SetName Root1, Root2;
scanf("%d %d\n", &u, &v);
/*
读入计算机编号的数组下标u-1
*/
Root1 = Find(S, u - 1);
/*
读入计算机编号的数组下标v-1
*/
Root2 = Find(S, v - 1);
if(Root1 != Root2){
/*
合并分属的不同集合
*/
Union(S, Root1, Root2);
}
}
void Check_connection(SetType S){
ElementType u, v;
SetName Root1, Root2;
scanf("%d %d\n", &u, &v);
Root1 = Find(S, u - 1);
Root2 = Find(S, v - 1);
/*
俩集合一样,那么已经联通.
*/
if(Root1 == Root2){
printf("yes\n.");
}else{
printf("no\n.");
}
}
void Check_network(SetType S, int n){
int i, counter = 0;
for(i = 0; i < n; i++){
/*
结点值小于0,多个根结点,意味着有未联通的集合.
*/
if(S[i] < 0){
counter++;
}
}
/*
只有一个根结点,那么表示整个集合都联通了.
否则,只输出联通的集合个数.
*/
if(counter == 1){
printf("The network is connected.\n");
}else{
printf("There are %d components.\n", counter);
}
}
/*
题外话:
集合S初始化.
每个元素都是独立的,每个元素都是自己的根结点,全部初始化为-1.
*/
void Input_connection(SetType S, int n){
for(i = 0; i < n; i++){
S[i] = -1;
}
}
TSSN的实现 (原始优化)
(TSSN:too simple sometimes naive)
第1版测试:

#这里是后续简化版本,union方法中:Root2第2个集合指向Root1第1个集合的根结点.
PTA测试结果:
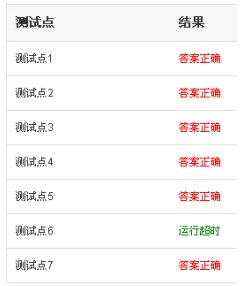
第2版测试:

#这里是后续简化版本改造,union方法中:Root1第1个集合指向Root2第2个集合的根结点.
PTA测试结果:

第3版测试:
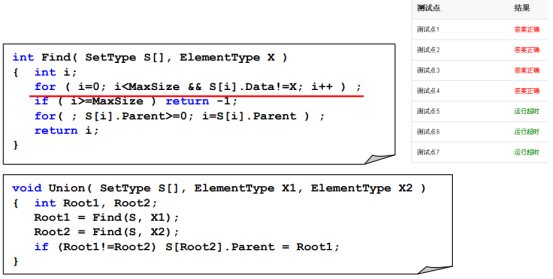
#这里是未简化前的原始版本进行PTA测试结果.
红色标记依然带来整个find函数的时间复杂度,如find到N次,时间复杂度为O(N的平方)。
====对于此效率的破坏,能否更快一点呢?继续下节”按秩归并”。
按秩归并 (union改进)(更快)

第1行:1指向2。
第2行:1指向3。
......
第n行:1指向n。
这里总会把第二个集合find(1)指向第一个集合。
这棵树在越长越高,做union,整棵树变成了单链表。
这一列操作,工作量最大的就是反反复复的find(1),每次都要从最底下的结点开始,一直往上去找其根结点,重复了N-1次之后,工作量就积累起来了。
比如当N=10的4次方时,N的平方数量级的算法肯定就会超时了。
这里设计两组数据来卡这件事,因为在标准实现中,是让第二个集合指向第一个集合,当然可能会有,第一个集合指向第二个集合。
所以还需设计另外一组数据,find顺序倒过来,不管是集合1指向集合2,还是集合2指向集合1,总有一组数据会卡的住。
方法:树的高度(O(N的X次方))

当两颗树高度不一致时,合并之前,最大高度是3。

树合并之后,最后,树的高度等于最高的这棵树的高度+1。

树如何才能不变高?
把矮的树贴到高树上,跟树的高度+1是无关的,而高的树的高度无变化。

在矮的树贴到高树上前,需要比较二者树的高度,除了根结点,在结构体中加一个阈值来存放其高度是合适的,现在存的都是父结点的下标,以元素值为下标存放,根结点-1除外。

这里把根结点设置成-1,-1不可能是任何一个元素的下标,可以和其他结点区分开了,任何负数也可以,可以提升此值的意义。

这里把根结点设置成”-树高”,但初始化时依然为-1。
一方面是负数标识,另一方面,数值代表树本身的高度。
因为初始认为每一台计算机都是独立的根结点,所以树的高度开始全部都为-1。

/*
按秩归并方法:树的高度
注意:如果Root2的高度>Root1的高度,A>B,那么-A<-B.
*/
void Union(SetName Root1, SetName Root2){
if(S[Root2] < S[Root1]){
S[Root1] = S[Root2];
}else{
if(S[Root1] == S[Root2]){
/*
要注意,这里存的是"负数-树高",如果树的高度要+1,那么这里要-1.
*/
S[Root1]--;
}
S[Root2] = S[Root1];
}
}
根据俩树的高度做判断,无论哪几个集合的高低,只要高度不同,那么作为最后的结果,最终树的高度是不变的。当俩树的高度相同,树的高度必须+1。
要注意,这里存的是”负数-树高”,如果树的高度要+1,那么这里要-1。
方法:树的规模(推荐)(NLog以2为底N的对数)

需要记录树的规模,即元素的总个数,以负数的形式存到根结点。
/*
按秩归并方法:树的规模(推荐)
*/
void Union(SetType S, SetName Root1, SetName Root2){
/*
集合2指向集合1.
把小集合贴到大集合中.
*/
if(S[Root2] < S[Root1]){
S[Root2] += S[Root1];
S[Root1] = S[Root2];
}
/*
集合1指向集合2.
把小集合贴到大集合中.
*/
else{
S[Root1] += S[Root2];
S[Root2] = S[Root1];
}
}
按高度归并:大树高度可能不需要改变。
按规模归并:大树的规模是会改变的,变成两颗树的和。
最坏情况下,不管是按高度还是按规模,最快情况都是把两棵树按高度或规模合并到一起,这种时候树的高度就不得不长大,如果整棵树的规模是N的话,那么这种合并会进行多少次呢?
最坏情况下的树高,Log以2为底N的对数,即使都去访问这颗树里面最下面的结点,重复N次的话,整个时间复杂度是NLog以2为底N的对数,而不是N的X次方。
========能否更快一点呢?继续下节”路径压缩”。
路径压缩 (find改进)(最快)
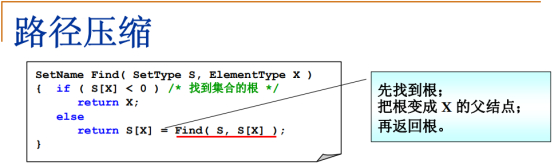
此find函数工作方式:判断传进的元素X,S[X]<0,意味着X已经是根了,直接返回X元素值,否则X还有父结点。
红色标记语句三个功能:
找到X的父结点S[X]所属集合的根(X和S[X]所属同一个集合)。
把根变成X的父结点,即:找到集合名称变成X的父结点
调用返回SetName,即返回根。
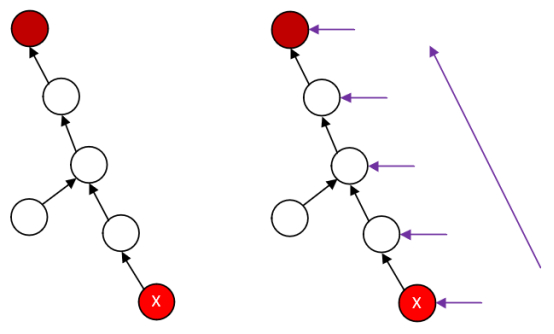
棕色结点为根结点。
第一次当调用find[X]后,首先X不是此集合的根,然后去集合中,递归去找X的父结点的根,把find[X]压入系统堆栈中,逐步解决X父结点的问题,再次父结点调用时,依然要检查X的父结点是否是根结点,不是就把X压入系统堆栈中,继续上述步骤往上走,一直到找到了真正的根结点,运行到find这个结点的时候,会发现S[X]是这个这个结点X,X小于0,直接返回X这个结点的父结点给X结点。
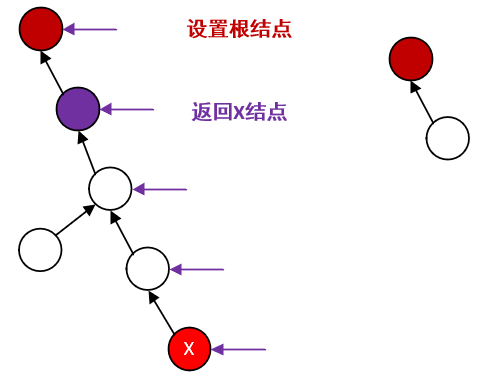
第1次返回结点,在返回之前,先把棕色结点设置为X的父结点。
对应第一个案例的状态。
此棕色结点本来就是X的父结点,所以这一步等于什么都没做,棕色父结点被return回去,并返回到下述蓝色结点这一层次,返回的仍然是棕色根结点。
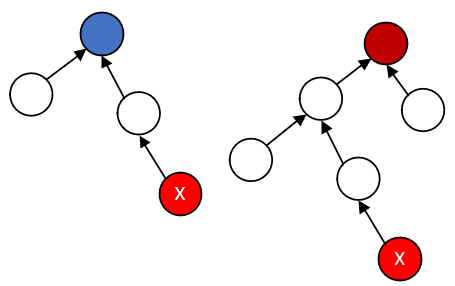
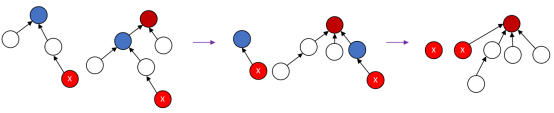
后续,继续上述步骤往上走,也把棕色结点变成其父结点,最终把这个棕色父结点返回给最下面的X结点,直接变成了X结点的父结点,这就完成了一个路径压缩的过程。
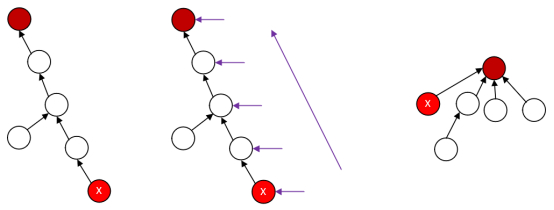
什么叫做路径压缩?非常直观的:在调用find函数的时候,不仅仅是X开始一路向上查找它的根结点,同时还把这个路径上的每个结点都直接贴到了根结点的下面,所以整棵树,至少这条路径被一下子压短了,这就叫路径压缩。
如果只调用一次find[X]时,其实只要把棕色结点返回即可,做上述那么多步骤好处在于,如果在程序中反复调用find,调用一次find麻烦一些,但是还需要find这条路径其他结点的话,就会变得非常划算。
需要注意的是,如果路径中的压缩结点太多的话,递归函数可能会使系统爆掉,但伪递归不会,因为机器的编译器会自动将伪递归变成循环。
为什么要做路径压缩呢?
建议把按秩归并算法和路径压缩算法,在PTA进行测试。
引理(路径压缩与按秩归并)

T(M,N)是最坏情况的时间复杂度。
M是带路径压缩的查找次数。
N-1是按秩归并的查找次数。
假设M大于N-1,其实是比较自然的假设。
在一次union之前总要做两次find,结论是说存在K1与K2,使得有这样一个不等式。
最坏情况的时间复杂度是Ma(阿尔法)函数,此函数跟M和N都有关系,Ma(阿尔法)函数既是这个时间复杂度的上限也是下限。
如果用渐进方式来表示的话,那这就是一个θ(SEI塔)的关系,是θ(SEI塔)(M)*a(阿尔法)。

这个a(阿尔法)函数跟Ackermann(艾克们)函数紧密联合在一起。
Ackermann(艾克们)函数有很多不同的定义,也是一个递归的定义,此函数有趣在于它可以以飞快的速度长到很大,它增长的速度有多快算以下这个A(2,4)。

非常恐怖的数字,幸亏a(阿尔法)不是这么大的数字。
此a(阿尔法)跟此数字如何联系在一起,以及Ackermann(艾克们)更多性质,更多看上述链接。
a(阿尔法)函数的定义如下:
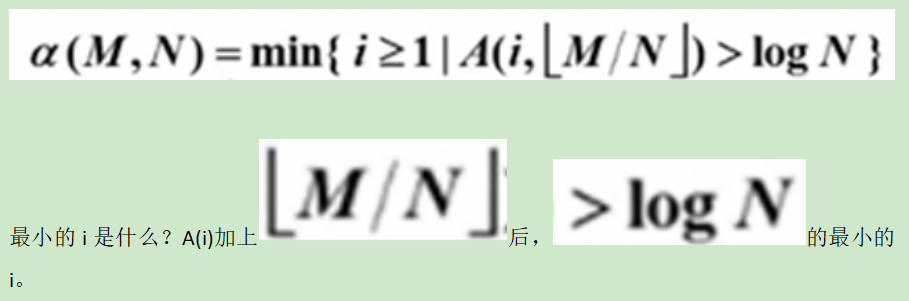



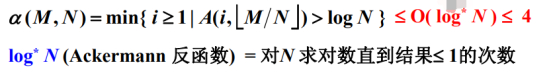
其实是否做路径压缩,根本区别在于在查找次数M前面,乘以常数还是一个LogN的问题,
当然,LogN是N的一个递增函数,当N趋于无穷大的时候,LogN是会趋于无穷大的,而常数不会变得,所以从理论效率来讲,做路径压缩比不做路径压缩要快的多。
就此题来说,N只有10的4次方这么大,LogN其实是一个很小的数字,所以比不出是否做路径压缩算法的优劣的。
如果把N再提高2个数量级,就可以看出是否做路径压缩算法的效率,当然编程语言也不同。
所以这道题的测试数据,要想充分体现路径压缩的优势是很难的。
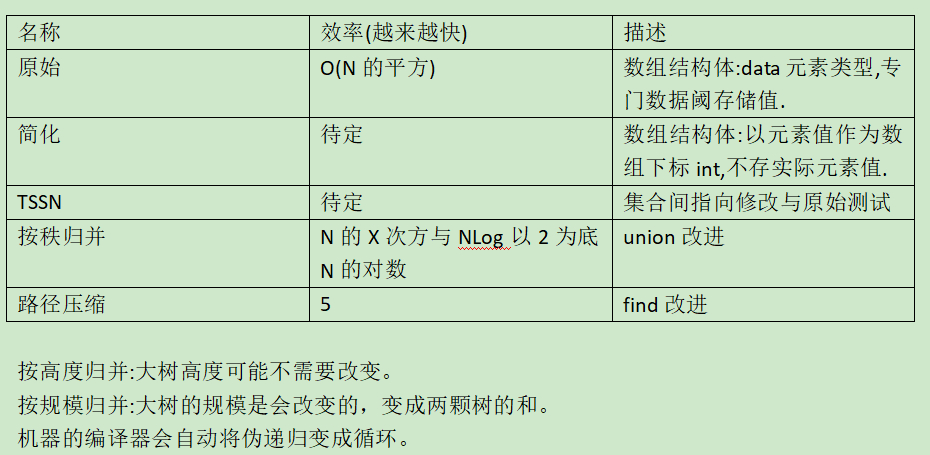
小总结
标题:(数据结构)文件传输File Transfer集合并查集应用-C语言实现
作者:yazong
地址:https://blog.llyweb.com/articles/2023/09/27/1695771873988.html