8.2.1 拓扑排序
AOV简介
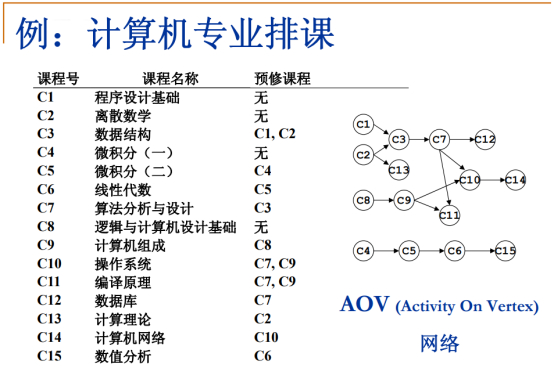
计算机专业的各个课程之间有依赖关系。
把课程列表转换为图,其中顶点代表课程,则从V到W有一条边代表V是W的预修课程。
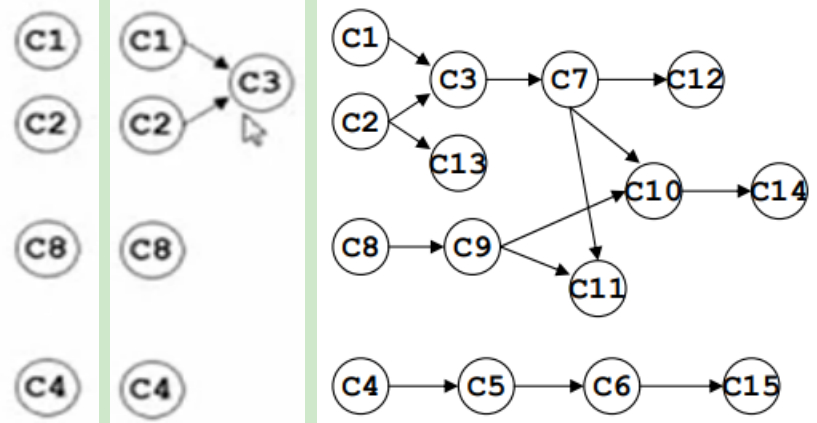
如何画图呢?先把没有预修课程的四个顶点画出来。
之后,依次画出课程之间的依赖关系。
此图叫做AOV网络,在此有向图中,所有的真实活动是表现在顶点上的,顶点和顶点之间的有向边表示了两个活动之间的先后顺序。
可以把这个问题抽象成一个拓扑排序问题。

合理的拓扑排序?
图中有环,就意味着V这个活动自己是自己的前驱结点,一定要在自己开始前结束,但这是一个不可能的事情,所以如果一个图中有环,那么就不可能得到一个合理的拓扑排序。
AOV:每个顶点表示的是一个事件或者一个活动。
AOE:每条边表示的是一道工序或者一个活动。
AOV如何产生拓扑排序DAG

这里给出一个AOV网络,如何把课程进行排序呢?先把无预修课程的课程先输出,其中的课程顺序无所谓。
在把图中的课程输出时,记得把顶点和边都抹掉,重点是要抹掉边。
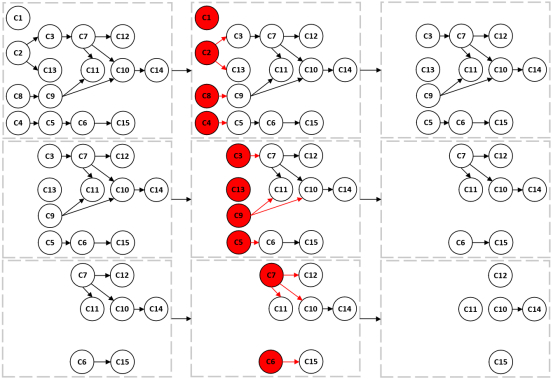
依次输出第1、2、3学期的课程。
(为啥C2收收录后,不能直接收录C3和C13,而是需要把其他入度为0的顶点先收录起来呢?看”问题”。)
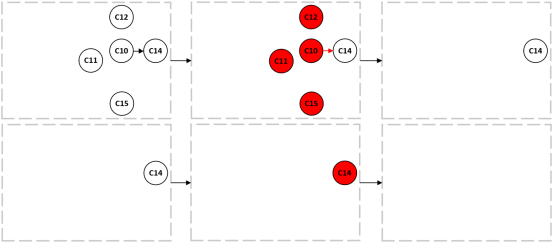
依次输出第4、5学期的课程。
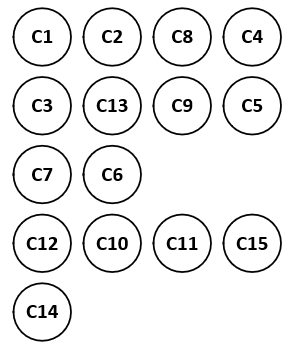
这样就完成了排课的过程。
这个过程实际上是一个拓扑排序的过程,这里输出的是没有前驱顶点的顶点。
如果知道某顶点没有前驱顶点?对于一个有向图来说,每个顶点有两个度,分别是入度和出度,没有前驱顶点的顶点的入度是0,也没有任何边会指向这个顶点。
那么这里选课,输出的同时,就是把没有预修课程的课程从原始图中彻底抹掉,不仅要抹掉顶点,重要的是抹掉边,在抹掉的同时,要把邻接点的入度都-1,邻接点也减少了一条边进来这个邻接点。
把图抹光的时候,一个正常的拓扑排序就产生了。
案例过程(未优化)(O(|V|^2))


案例过程(优化)(检测有向无环图)(稀疏图O(|V| + |E|)稠密图O(|V|^2 + |E|))

任何一个入度为0的顶点,放到一个特殊的容器中,数组、链表、堆栈、队列都行。
在下一次找入度为0的顶点时,就不用去扫描所有的顶点集合,而是去到这个容器中取即可。
那么时间复杂度就变为常数级。
如果要把入度为0的顶点抹掉,那么意味着要把这个顶点的邻接点的入度都要-1,在邻接点-1的同时要把这个邻接点放在容器队列中,下次可以取出使用,否则啥都不做。

源码(优化)
#include<stdio.h>
/*
图-拓扑排序-邻接表存储-优化-容器收集
*/
int main(void){
return 0;
}
/* 对Graph进行拓扑排序, TopOrder[]顺序存储排序后的顶点下标 */
bool TopSort(LGraph Graph, Vertex TopOrder[]){
int Indegree[MaxVertexNum], cnt;
Vertex V;
PtrToAdjVNode W;
Queue Q = createQueue(Graph->Nv);
/* 初始化Indegree[] */
for(V = 0; V < Graph->Nv; V++){
Indegree[V] = 0;
}
/* 遍历图,得到Indegree[] */
for(V = 0; V < Graph->Nv; V++){
for(W = Graph->G[V].FirstEdge; W; W = W->Next){
/* 对有向边<V, W->AdjV>累计终点的入度,在后续逐渐减为0 */
Indegree[W->AdjV]++;
}
}
/* 将所有入度为0的顶点入列 */
for(V = 0; V < Graph->Nv; V++){
if(Indegree[V] == 0){
AddQ(Q, V);
}
}
/* 下面进入拓扑排序 */
cnt = 0;
while(!IsEmpty(Q)){
/* 弹出一个入度为0的顶点 */
V = DeleteQ(Q);
/* 将V存为结果序列的下一个元素 */
TopOrder[cnt++] = V;
/* 对V的每个邻接点W->AdjV */
for(W = Graph->G[V].FirstEdge; W; W = W->Next){
/* 若删除V使得W->AdjV入度为0,入度逐渐-1 */
if(--Indegree[W->AdjV] == 0){
/* 则该顶点入列 */
AddQ(Q, W->AdjV);
}
}
}
if(cnt != Graph->Nv){
/* 说明图中有回路, 返回不成功标志 */
return false;
}else{
return true;
}
}
8.2.2 关键路径 (拓扑排序重要应用)
AOE简介

AOV:每个顶点表示的是一个事件或者一个活动。
AOE:每条边表示的是一道工序或者一个活动。
AOE网络一般被用作于安排一个很庞大的项目,这个庞大的项目会分成很多道工序,工序与工序之间是有先后依赖关系的,AOE网络用来解决这类问题。
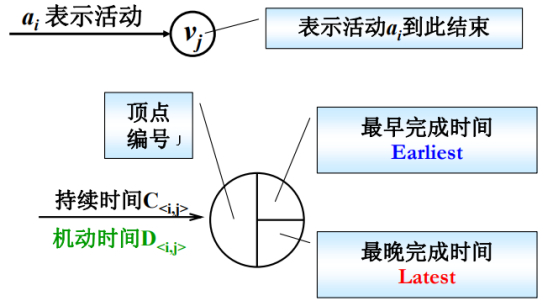
正在AOE网络中,顶点Vj表示这个活动,Ai活动是表示在边上,活动达到顶点时表示活动结束。
边分两块:
上块表示活动的持续时间/实际执行时长,表示这个小组完成这道工序一共需要多少天的时间。
上块表示活动的机动时间。
每个顶点分三块:
顶点编号:Vj中的j这个编号。
最早完成时间:所有的任务最早的完成时间。
最晚完成时间:所有的任务最晚的完成时间。
案例过程
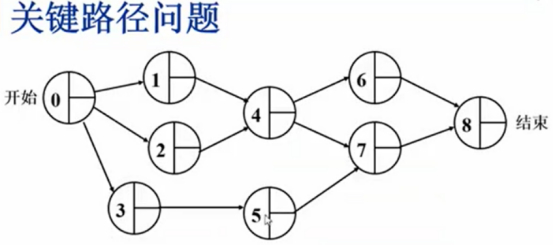
这是整个project,标记了项目开始、项目结束的顶点,每条边代表一件事,每件事情相互依赖的顺序完成之后,到达结束顶点作为结束。
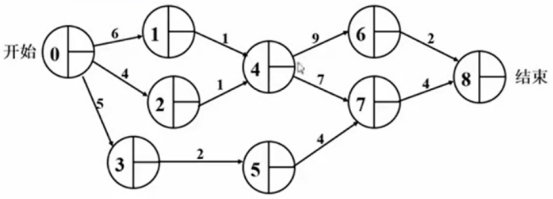
第一件事:首先要知道每一道工序需要的天数/持续时间是多少。
比如4-6、4-7(仅标记,并不是实际的)开工必须等1-4、2-4完工才能开工。
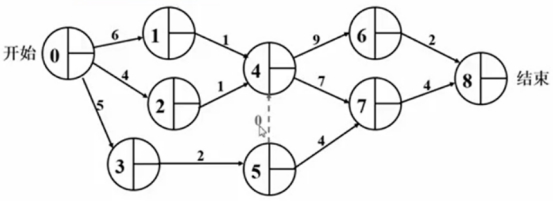
更复杂情况,如果4-6、4-7不仅要等1-4、2-4完工,还得等3-5完工才能开工。
现在5-7开工跟1-4、2-4是没关系的,5-7开工只关心3-5。
但4-6、4-7需要等1-4、2-4以及3-5完工才能开工,如何解决?
可以把45顶点合并,画虚边(有箭头,标记4-7需要等3-5完工才能开工),把持续时间/权重标记为0。
这样就可解决4-6、4-7需要等1-4、2-4以及3-5一起完工才能开工。

先算每个顶点的最早完成时间earliest值:
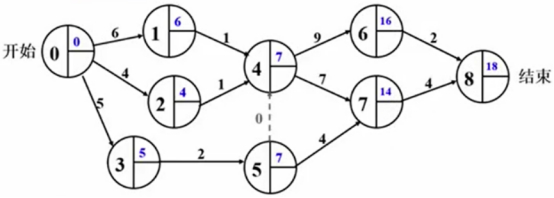
初始点的最早完成时间earlier值是0,每次往后面推的时候,如果后面结点的前一步结点的ij是一条边的话,那么前一步结点的earlier值加上这条边的权重,就等于后面结点的earlier值,当earlier值不确定,比如有三条边指向后面结点时,取所有边中最大的时间earlier值,比如结点4,1-2是6+1=7,2-4是4+1=5,最终结点4的earlier值取7。

作为项目负责人,需要知道哪些组的工期一天都不能耽误,哪些组是中间可以拎出去干其他事情的,也就是可以有机动时间可以拎出去干其他事情。
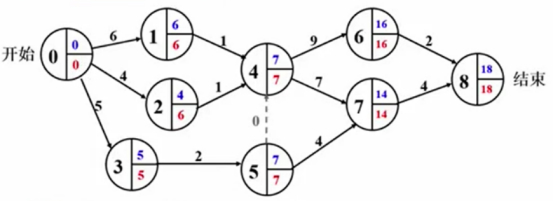
倒推开始,先算每个顶点的最晚完成时间latest值:
从最后一个顶点的latest等于earliest,从后往前推每个顶点的latest。如果i结点和j结点之间有一条边的话,那么用j结点的latest减去i结点和j结点之间的持续时间/权重,那么就得到i结点的latest。
当latest值不确定,选择最小的,
比如对于顶点5来说,顶点7可以最晚14天完工,而5-7只需4天就可以完工,那么顶点5只需要在第10天完工即可,但是不行,因为5-4这条边还在,所以顶点5必须在第7天开工和完工,否则整个工期就要延误,所以二者必须选择最小的latest值,那么0-1、0-2、0-3同理。
那么这里,比如0-1、1-1这些组的工期是一天都不能耽误的。

此时算机动时间:哪些组是中间可以拎出去干其他事情的,也就是可以有机动时间可以拎出去干其他事情。
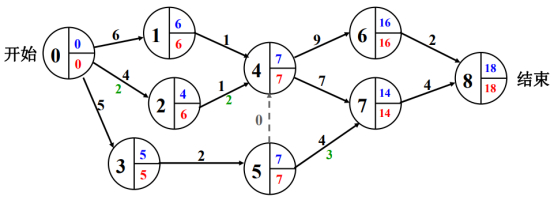
比如0-2,结点i和结点j之间有一条边的话,用结点j的latest:6减掉结点i的earliest:0,再减去结点i和结点j之间边的持续时间/权重:4,就等于机动时间2,这里结点i到结点j只需要4天就可以完工,另外2天为机动时间,可以另外做别的事情,那么2-4、5-7同理。
重要/最终概念
