其中每一项是叫aiX^i，这样的一个多项式，它的基本运算就包括两个多项式，相加、相乘、相减等这些运算。

那么，此时需要思考，如何用程序语言来表示这样的一个多项式？以及实现相应的运算操作？

多项式如何表示？

在程序设计语言中，要表示一个问题，

首先要分析一下，这个问题的关键数据、关键信息在哪里？

对多项式来讲，需要注意的关键信息:

一个是项数、包括它的最高指数;

另外一个是，重要的是要表现多项式的每一项，而多项式的每一项的关键信息，又是每一项的的系数和指数。

方法1:顺序存储结构-直接表示-结构数组

首先可以用数组来表示多项式的有关信息，多项式的每一项可以用一个分量来表示，这个分量主要表示每一项的系数，指数可以对应于这个分量的下标。

比如，可以用a这个数组来表示一个多项式，a[i]就可以表示项的系数，而这个i就是对应的指数。

可以直截了当的使用这样一个数组来表示。

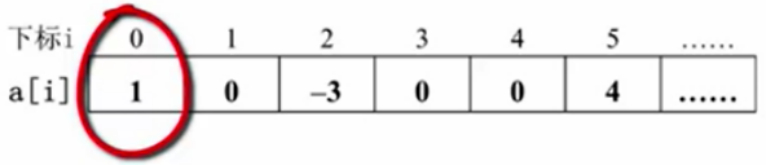
数组分量有6项，其中下标为0的这一项，它的值是1，是代表指数为0的那一项的系数。

下标是1的这一项，值是0，代表x^1这一项，系数是0。

以此类推，那么这里就可以很简单的用6个分量来表示3个项所组成的这样一个多项式，表示方法也很简单。

比方说，多项式相加，就变成两个对应数组的对应分量的相加。

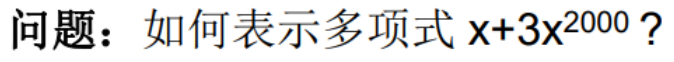
但是这里面也有一些问题，这里要用多大的数组来表示这样一个多项式呢？

显然，至少要用2001个分量这样的一个数组来表示，而这2001个分量，其实，只有2项是非0的，其他全是0。这样的一种表示方法会造成空间的巨大浪费。

而且做加法运算的时候，需要做for循环，那么从0开始加到2000，实际上很多计算是在加无效的0，所以这种方法虽然方便，但是有很大的问题。

为什么要把所有零项、非零项、系数为零的、非零的，都要表示进来呢？

有没有可能只引入非零项，见方法二”顺序存储结构表示非零项”。

方法2:顺序存储结构-(只)表示非零项

基本思路:只表示非零项。

每个非零项实际上有两个信息:一个是系数，一个是指数。

(“方法1:顺序存储结构直接表示”的每个分量是系数，这里的分量是系数和指数。)

可以把多项式看成一个由系数跟指数二元组组成的一种集合，可以用结构数组表示这样的多项式。

案例1:结构数组-按指数有序存储

这个案例可以简单的用结构数组来进行表示。

第1个多项式，标红的是第1个结构数组的第零个分量。

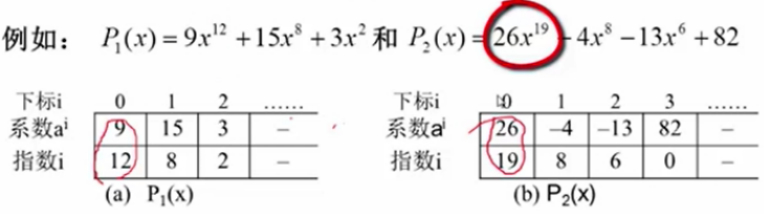
第2个多项式，标红的是第2个结构数组的第零个分量。

用此种方法，只需要表示非零项就可以了。

很多零项，都可以省下来，对于“方法1:顺序存储结构直接表示”中的下述问题。

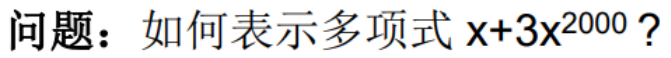
只需要两个分量表示即可，空间显然大大节省。

但这样的表示法，运算是否方便？

前提是:多项式中的每一项”按照指数大小有序进行存储”。

在此例子中，把指数大的排在了前面，指数小的排在了后面，让其递减地去存储。

但这样的做法，如何做加法运算呢？

案例2:结构数组-加法运算

P1实际上是三项，P2有四项。

按照指数递减的顺序进行排列，那么加法运算，可以从头开始，比较两个多项式当前最大指数的那一项。

基本方法: 从头开始比较，看哪个指数高，就把哪个指数高的项拿出来，如指数相等，那么对应系数相加 。

这是一种节省空间的方法，而且 操作效率也不差 。

P1的第一项和P2的第一项，这两个对象相加的结果，一定是X^19，那么P2的第一项作为和的结果，第一项输出了。

比较P1的第一项X^12，跟P2的第二项X^8，输出大的X^12，即(9,12)。

比较P1的第二项X^8与P2的第二项X^8，指数相同，系数不同，系数相减，指数不变，输出(11,8)。

比较P1的第三项X^2与P2的第三项X^6，输出大的X^6，即(-13,6)。

比较P1的第三项X^2与P2的第四项X^0，输出大的X^2，即(3,2)。

此时P1结束了，就直接把P2剩下的内容(82,0)输出即可。

最终得到这样一个多项式，显然，这样一种结构，就是用指数和系数构成的结构，存储在数组中，来表示非零项。

案例3:链表结构-存储非零项

在这个链表中，结点包含的主要信息:两个数据域(系数(coef)、指数(expon))、指针域(把不同的项串起来)。

同样，排列的时候，仍然可以按照指数递增/递减的一定顺序排列。

可以定义一个这种结构，叫PolyNode，其中包括了系数、指数以及指针域。

前面的例子，如果有链表存储的形式，可以表示成这两种链表，是按照指数递降的顺序进行排列的。

同样，加法运算，整个逻辑过程跟前面两个数组的运算是一样的，也就是，分别指向多项式的头，然后比较指数大小，大的输出，想等的话，系数相加。

小总结