
前面的多项式的问题给我们什么启示呢?
首先,同一个问题可以有不同的表示方法和存储方法。
在数据结构中最常见的两种方法:数组存储、链表存储。
多项式问题,其他一系列问题,都是有共性的。
目标:是想管理一个有序的线性序列。
那么把其归结为”线性表”的问题。

线性表的抽象数据类型描述

对于线性表来说,可以用一种抽象数据类型来进行描述。
所谓的抽象类型实际上包含了两个要素:
一个是这个类型所包含的数据对象集是什么?
另一个是,在这个对象集上面,有什么操作?
假定,线性表类型叫List,对其中的一个线性表叫L,它里面的元素X有个类型叫ElementType,这个类型可以是整型,也可以是实型,也可以是结构,统称为ElementType,还用整数表示一个元素在表中的位置。
线性表的顺序存储(数组)实现
最简单的一种存储方法,就是顺序存储,可以用数组来实现。
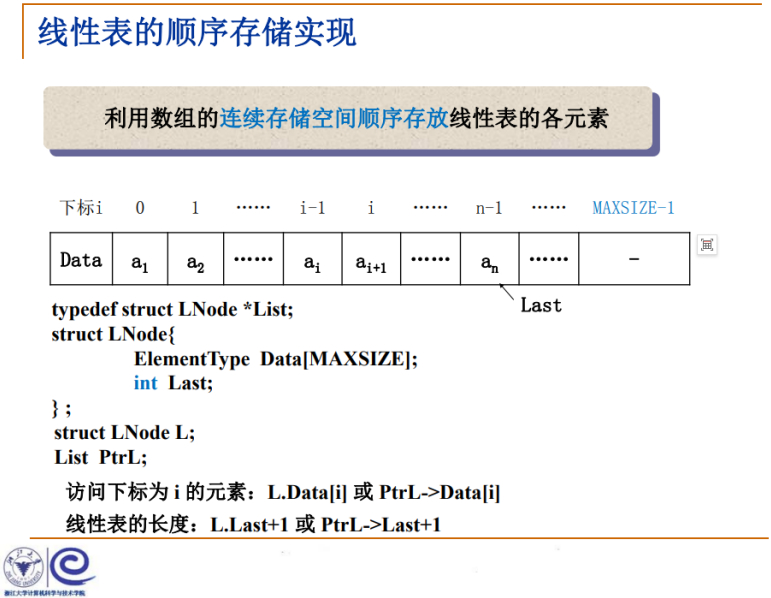
线性表中的序列(a1,a2,a3...ai-1,ai),从小标为0的位置,可以按这个顺序存储在数组中。
这样一种存储方法,在数据结构的定义应该是怎样的?
typedef struct LNode *List;
//下述结构抽象的实现一个线性表
struct LNode{
//数组
ElementType Data[MAXSIZE];
//最后一个元素所在的位置:指针,指示在这个数组里存放的、线性表的最后一个元素所在的位置
int Last;
};
/**
访问下标为i的元素:L.Data[i]或PtrL->Data[i]
线性表的长度:L.Last+1或Ptrl->Last+1
*/
struct LNode L;
List PtrL;
主要操作的实现:初始化(建立空的顺序表)
/*
主要操作的实现:初始化(伪代码)
*/
List MakeEmpty(){
List Ptrl;
/*
malloc申请线性表这样一个数组结构的空间
把结构的Last设为-1,因为Last代表最后一个元素。
Last=0,代表这个表里有一个元素放在第一个位置。
没元素设为-1.
*/
Ptrl = (List)malloc(sizeof(struct LNode));
Ptrl->Last = -1;
//返回此结构的指针
return Ptrl;
}
主要操作的实现:查找
/*
主要操作的实现:查找(伪代码)
ElementType X:在下述线性表中,通过循环找X所在的位置
Ptrl:线性表结构的指针
*/
int Find(ElementType X,List Ptrl){
int i = 0;
/*
这里查找成功的平均比较次数为(n+1)/2,平均时间性能为O(n)。
运气好,第一个就找着了;运气不好,最后一个找着了。
*/
while(i <= Ptrl->Last && Ptrl->Data[i]!=X){
i++;
}
//如果没找到,那么返回-1.
if(i > Ptrl->Last){
return -1;
}
//如果找到后,那么返回的是存储的位置.
else{
return i;
}
}
线性表的顺序存储的插入和删除
插入
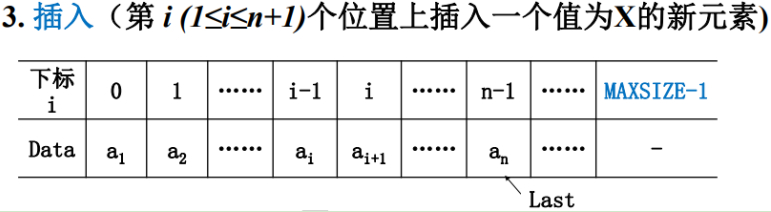
目标:在线性表的第i个位置上面插入X这个元素。
这里的第i个位置指的是i的值从1到n+1,
1就插在线性表的头上;n+1是插在线性表的最后。
但是线性表是在数组里表示的,下标是从0开始的,那么,这个元素要放在哪个位置呢?
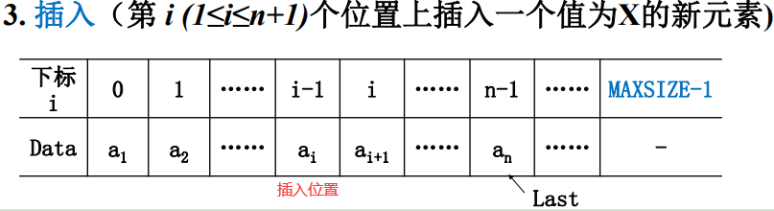
如果要把新插入的元素X放到i-1这个位置,那么如何办呢?
这些元素是连续存放的。
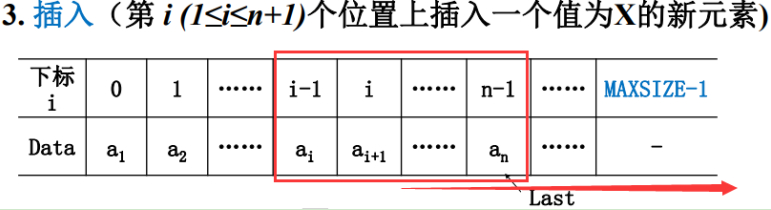
首先要做的事情,是要把i-1之后的这些元素全部往后挪一位,腾出i-1这个位子来,然后再往里面放元素。
所以这个操作的第一个要做的事情是:先移动。
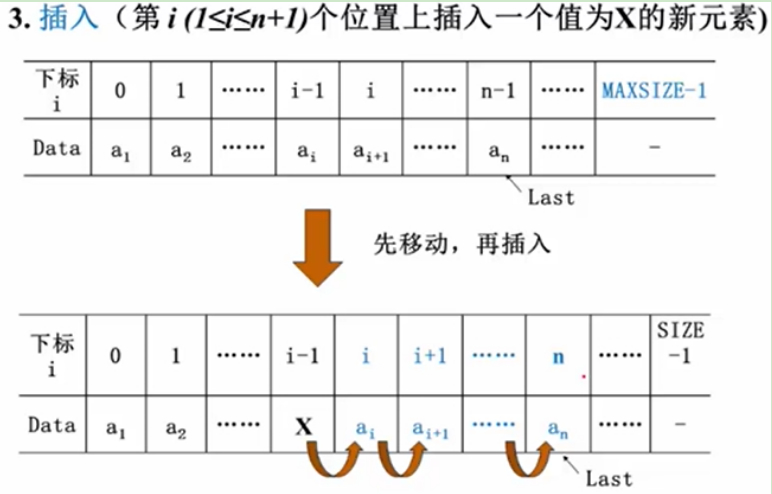
(Last指向的下标应是n+1)
每一个元素都往后挪,显然有个循环就可以了。
但是,这里应该是从后面开始挪,按顺序,把最后一个往后挪,倒数第二个往后挪等,否则,这个算法是不对的。
/*
插入操作实现
X要插入在这个链表Ptrl的第i个位置
*/
void Insert(ElementType X,int i,List Ptrl){
int j;
/*
表空间已满,不能插入
MAXSIZE是数组的大小
因为数组下标是从0开始的,所以最后一个元素的下标是MAXSIZE-1.
正好等于数组的最后一个元素.
*/
if(Ptrl->Last == MAXSIZE-1){
printf("表满");
return;
}
/*
检查插入位置的合法性
是否落在1到n+1之间
*/
if(i<1 || i>Ptrl->Last+2){
printf("位置不合法");
return;
}
/*
从Last最后一个元素开始做,不能从i-1开始做.(j--到i-1)
把前面的放到后一个元素,逐次放.
整个算法的时间复杂度就在这个for循环里面:
平均移动次数为n/2
平均时间性能为O(n)
注:如果有些绕,那么把具体数字带进去算.
*/
for(j=Ptrl->Last;j>=i-1;j--){
Ptrl->Data[j+1]=Ptrl->Data[j];
}
/*
将a1~an倒序向后移动
之后的所有元素都往后挪了
挪了之后腾出了i-1这个位置,也就是第i个位置,那么这个时候把X放进去.
*/
Ptrl->Data[i-1]=X;
/*
新元素插入
由于放入X元素之后多了一个元素,所以Last++
*/
Ptrl->Last++;
/*
Last仍指向最后元素
*/
return;
}
删除
这里要删除i位置为1到n之间的元素,对应的数组下标就是0到n-1。
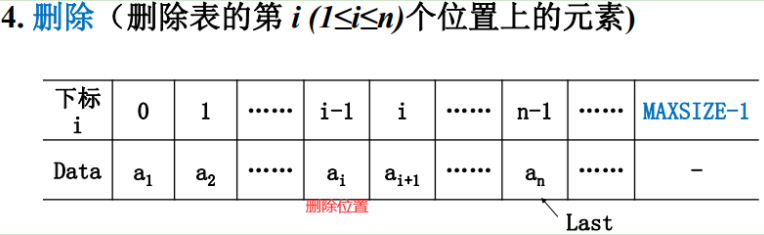
这就位置着要删除的这个ai元素的位置i-1空出来了。
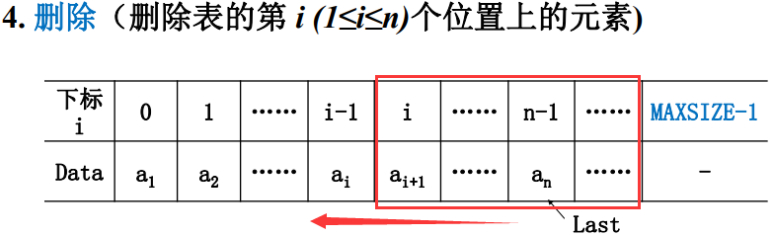
那么就要把i位置之后的这些元素全部往前移动,按照从左向右的顺序往前挪。
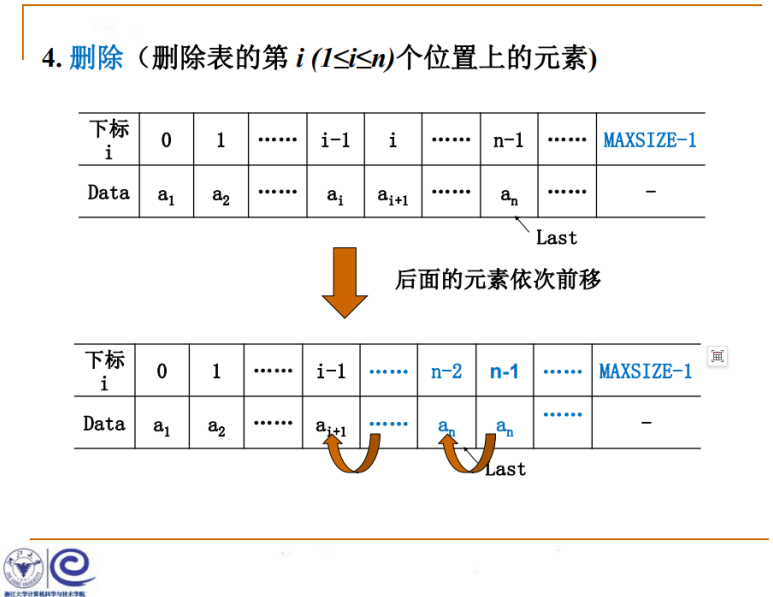
/*
删除操作实现
X要在这个链表Ptrl的第i个位置删除,后面的元素全部往前移动.
*/
void Delete(int i,List Ptrl){
int j;
/*
检查空表以及删除位置的合法性
*/
if(i<1 || i>Ptrl->Last+1){
printf("不存在第%d个元素!",i);
return;
}
/*
将a(i+1)~an顺序向前移动
把后面的放到前一个元素,逐次放.
平均移动次数(n-1)/2
平均时间性能O(n)
注:如果有些绕,那么把具体数字带进去算.
*/
for(j=i;i<=Ptrl->Last;j++){
Ptrl->Data[j-1] = Ptrl->Data[j];
}
/*
Last仍指向最后元素
*/
Ptrl->Last--;
return;
}
线性表的链式存储(链表)实现
存储

当线性表使用数组存储的时候,两个相邻的元素不仅逻辑上是相邻的,而且物理上也是相邻的,当插入和删除时,都要把数组中的元素往后挪动或往前挪动。
但是在链表中,只需要修改链表就可以了,不需要对很多的元素进行挪动。

求表长:
在数组中,找序号=i的元素,只需要a[i-1]即可。
在线性表中,求线性表的长度,只需要找到Last指针即可
如要在一个链表中,如何查找第i个元素以及链表的长度是多少?
/*
链表存储结构:
求表长
方法:链表遍历-从头到尾.
*/
int Length(List Ptrl){
//临时指针P指向表头
List P = Ptrl;
int j = 0;
//p不为null
//时间复杂度是链表的长度为O(n)
while(p){
//链表指针往后挪一位
p = p->Next;
//计数器j对应元素的位置/当前元素所在的长度
j++;
}
return j;
}
查找
在数组中,直接返回a[i-1]即可找到元素。
但是在链表中,还是需要一个个元素来遍历。
链表存储结构:按序号查找
/*
链表存储结构:按序号查找
方法:链表遍历-从头到尾.
平均时间复杂度为O(n)
*/
List FindKth(int k,List Ptrl){
//临时指针P指向表头
List p = Ptrl;
int i=1;
while(p!=NULL && i<k){
//链表指针往后挪一位
p = p->Next;
//计数器i对应元素的位置
i++;
}
if(i==k){
//查找到直接返回当前元素
return p;
}else{
return NULL;
}
}
链表存储结构:按值查找
/*
链表存储结构:按值查找
方法:链表遍历-从头到尾.
平均时间复杂度为O(n)
*/
List Find(ElementType X,List Ptrl){
//临时指针P指向表头
List p = Ptrl;
while(p!=NULL && p->Data != X){
//链表指针往后挪一位
p = p->Next;
}
//p=null那么肯定没找到
return p;
}
插入

首先构造新的结点s,用malloc函数申请一块空间。
接下来,要找到插入的前一个结点i-1,并用p指向它。
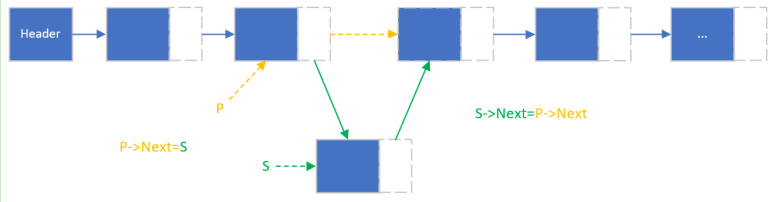
此时,按顺序做两件事(并不能相反,否则会导致S->Next=S):
S->Next=P->Next
P->Next=S
通过这两个赋值语句就可以修改两个指针方向,当然,就把新的结点插入进去了。
/*
链表存储结构:插入操作
*/
List insert(ElementType X,int i,List Ptrl){
List p,s;
/*
新结点插入到表头
i-1=0,0这个位置在链表里面是不存在的.
如这个结点要插在表头,那么就需要做特殊处理.
当插入表头后,那么整个链表的头指针就发生了变化,这样通过Insert方法调用返回的就是新的头指针.
*/
if(i==1){
/*
申请、填装结点
*/
s = (List)malloc(sizeof(struct LNode));
//设置新结点s中的值
s->Data = X;
s->Next = Ptrl;
return s;
}
/*
按序号查找第i-1个结点
*/
p = FindKth(i - 1,Ptrl);
/*
未找到/不存在第i-1个结点,不能插入
*/
if(p == NULL){
printf("参数i错误!");
return NULL;
}
//这里的平均查找次数为n/2,平均时间性能为O(n).
else{
/*
申请、填装结点
*/
s = (List)malloc(sizeof(struct LNode));
//设置新结点s中的值
s->Data = X;
/*
新结点插入在第i-1个结点的后面
*/
s->Next = p->Next;
p->Next = s;
/*
注意这里返回的是新的链表的头指针,但是这个头指针是不变的。
*/
return Ptrl;
}
}
删除

先看一个错误案例:

因为是单向链表,那么必须找到前一个结点,指针指向被删除的结点位置,仅通过赋值语句就可以实现。
如果单纯的这么做,找到要删除结点的前一个结点p,并把p结点的指针指向要删除结点的后一个结点,再直接删除要删除的结点,那么这样是有问题的。
首先,被删除结点是通过malloc函数申请的空间,还回去要使用free函数。
另外,被删除结点的指针还指向着后一个结点。
正常的方案:
此时,按顺序做两件事(并不能相反,否则会导致S=S->Next):
S=P->Next
P->Next=S->Next
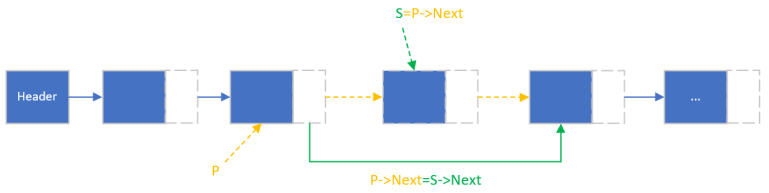
释放S,这样的话,内存才不会泄露。

/*
链表存储结构:删除操作
*/
List Delete(int i,List Ptrl){
List p,s;
/*
删除链表的第一个结点:表头
*/
if(i == 1){
/*
s指向表头结点
*/
s = Ptrl;
if(Ptrl != NULL){
/*
表头设置成原表头的下一个结点
*/
Ptrl = Ptrl->Next;
}else{
return NULL;
}
/*
释放/删除原表头结点
*/
free(s);
return Ptrl;
}
/*
按序号查找第i-1个结点
*/
p = FindKth(i - 1,Ptrl);
//这里的平均查找次数为n/2,平均时间性能为O(n).课程是2/n的时间复杂度?
if(p == NULL){
//本身就是空的肯定删除失败
printf("第%d个结点不存在",i-1);
return NULL;
}else if(p->Next == NULL){
printf("第%d个结点不存在",i);
return NULL;
}else{
//s指向第i个结点
s = p->Next;
//从链表中删除s结点
p->Next = s->Next;
//释放被删除结点s
free(s);
/*
注意这里返回的是新的链表的头指针,但是这个头指针是不变的。
*/
return Ptrl;
}
}
广义表
"复杂" 链表(一元/二元多项式)

二元多项式,里面包含两个变量。
可以把二元多项式看成是一个关于X的一元多项式。
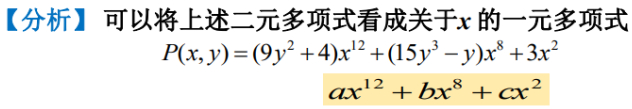
X的12次方在一元多项式中是个系数、常量,但是在这里,它是一个关于Y的一元多项式,所以可以仿照一元多项式的一种表示方法用链表把它表示出来。
在原来的一元多项式中,X的12次方和X的8次方的系数是常量,但是的一元多项式,可以形成链表来表示。
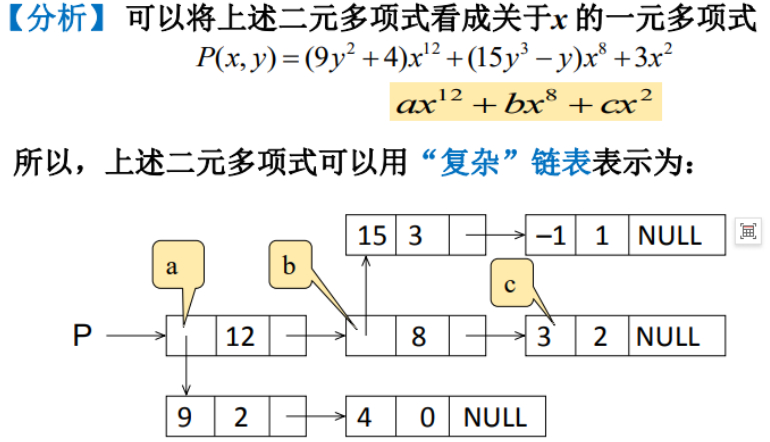
可以发现,P指向的多项式的第一项应该是12,现在又是一个指针,指向了一个关于Y的一元多项式,也就说,原来这个位置相当于都是常量的位置,现在变成指针了,指向了另外一个一元多项式。
这种表称之为广义表,所以广义表它是线性表的一种推广。
在一般线性表里,我们的元素都是一些单元素,但在广义表里,我们的这些元素不仅可以是单元素,也可以是另外一个广义表。

在广义表构造的时候,会碰到的问题,一个域可能是不能分解的单元,有可能是一个指针。
那么在C语言中提供的方案是联合union,可以把不同类型的数据组合在一起,可以把联合union的这个空间理解成某种类型。
如果要区分不同的联合union类型,那么可以再加个tag,然后和联合union组合在一起,使用Tag来区分union这块空间。

/*
广义表:"复杂"链表
*/
typedef struct GNode *GList;
struct GNode{
/*
标志域:0表示结点是单元素,1表示结点是广义表(一个指针指向另外一张广义表)
*/
int Tag;
union{
/*
单元素数据域Data与子表指针域SubList复用,
即共用存储空间.
*/
ElementType Data;
GList SubList;
} URegion;
/*
指向后继结点
*/
GList Next;
}
多重/十字链表(稀疏矩阵/树/图)

注:比上节更复杂的链表结构,更多的指针。

假如,要表示一个大学里面每个学生选了什么课程,什么课程是被哪些学生选的,那么可以使用二维数组来表示选课的一种记录,比方说行代表课程、列代表学生。
那么对于学校来说,学生可能上万人,课程几千门,所以这是一个巨大的矩阵,可以想象得出,这个矩阵中的0是非常多的,非零项是非常少的,那么像这种矩阵,叫稀疏矩阵,它明显的存在一个空间浪费的情况。
前面学过的一元多项式X+3X的2000次方,如简单地用数组来直接存储,就会占用了大量的空间存0。
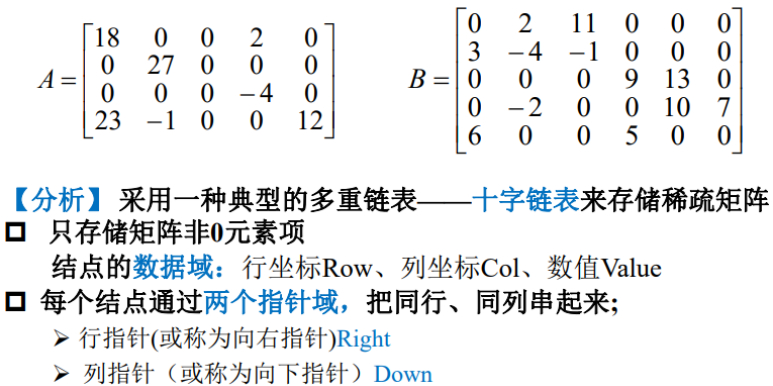
那么,如何在稀疏矩阵中存储非零项呢?
非零项的信息主要是:行、列、数值,那么可以把这些关键信息做成一个结点。
矩阵意味着,行与行、列与列之间是有关系的,如何建立关系呢?
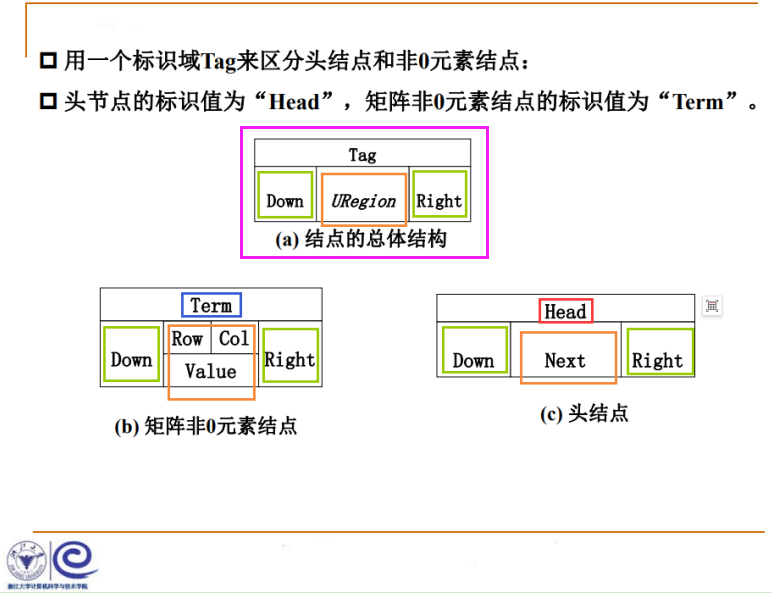
每个结点通过两个指针(行指针/向右指针Right、列指针/向下指针Down),把同一行、同一列的元素串起来,每个结点既属于某一行,又属于某一列。
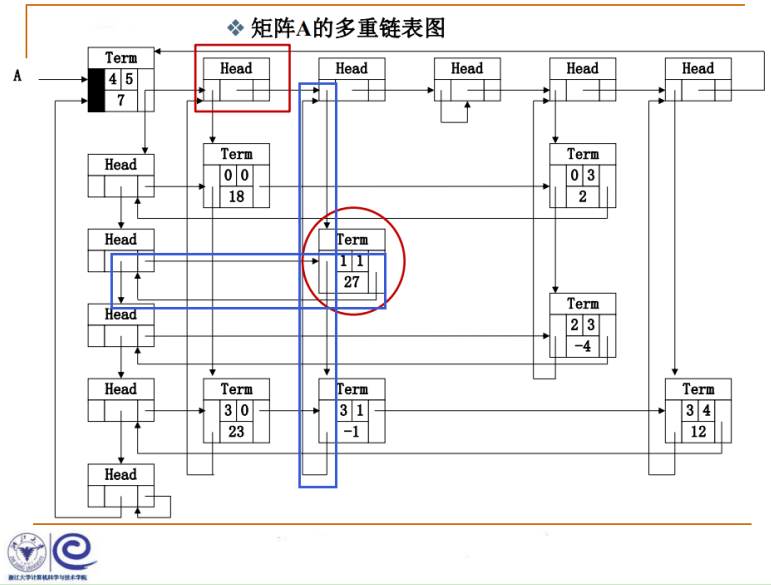
Term类型有两个指针,一个指向同一行,一个指向同一列,同一行的指针,它把同一行同一列都设计成一个叫 循环链表 ,所以每个结点属于某一行(同一行的循环链表)也属于某一列(同一列的循环链表),形成了这样的十字结构,所以叫做十字链表。
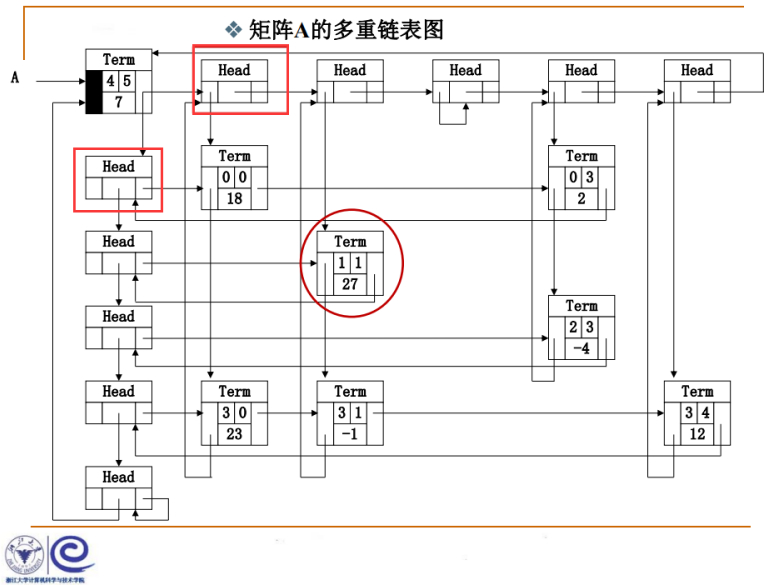
Head类型,作为行这个链表的头结点,也作为列这个链表的头结点。
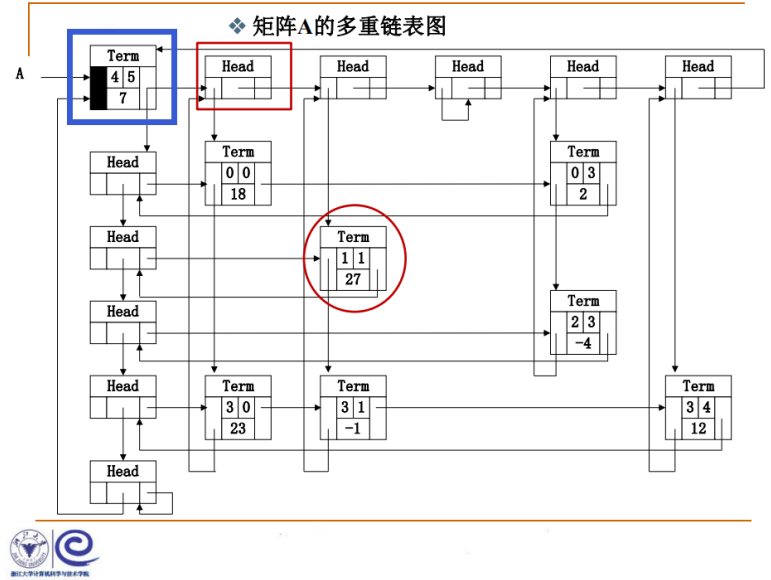
左上角的Term是整个稀疏矩阵的入口,结点结构跟前述Term是一样的,Term代表稀疏矩阵中的非零项。
4代表这个稀疏矩阵总共有4行,5代表这个稀疏矩阵总共有5列,非零项总共有7项,代表一个4行5列的稀疏矩阵。
通过指针就可以找到所有列的头结点、所有行的头结点,所以这是整个稀疏矩阵的入口结点,通过它可以知道整个矩阵的信息。
/*
广义表:多重/十字链表
(课程未提供此伪代码:自己编写待修改)
*/
typedef struct GNode *GList;
struct GNode{
/*
指向列方向结点的指针
*/
GList Down;
/*
指向行方向结点的指针
*/
GList Right;
/*
标志域:0表示结点是Head头结点,1表示结点是Term非0元素结点.
*/
int Tag;
union{
/*
Data1为Head中的内容,
Data2为Term中的内容,
即共用存储空间.
*/
ElementType Data1;
ElementType Data2;
} URegion;
}
Head结点和Term节点的共同点(浅绿色):指向同一行的指针和指向同一列的指针。
Head结点和Term节点的不同点(浅棕色):内容不同。
可以建立联合union结构把上述(浅棕色)不同的内容建立在一起,那么最终就是上述(紫色)总体结构。
上述就是稀疏矩阵用十字链表解决的一种基本思路。
小总结
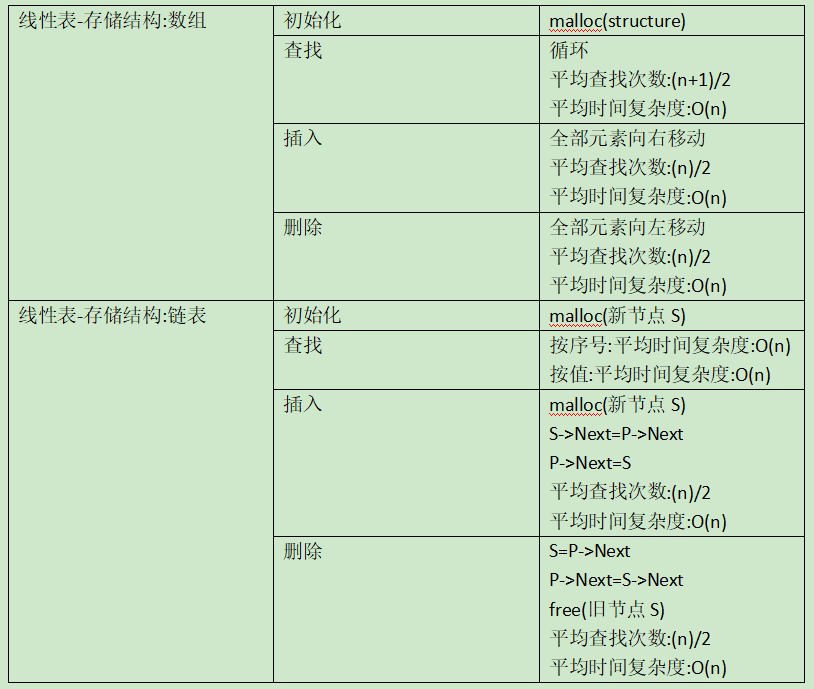
此章节首先给出的是一种抽象数据类型的描述,然后就需要关注的是线性表是如何存储的,以及线性表是如何操作实现的。


标题:(数据结构) 第二讲-线性结构(2.1.2线性表及顺序存储)
作者:yazong
地址:https://blog.llyweb.com/articles/2023/07/01/1688148688691.html