3.2.1 二叉树的定义及性质

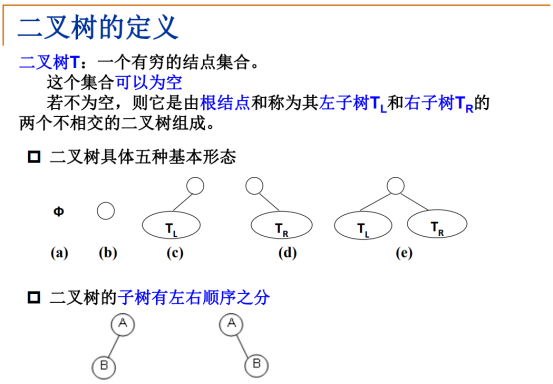
可以把二叉树理解成度为2的树，但是跟一般树相比，就在于，二叉树的子树有左右之分，而一般树是没有左右之分的。

A空树

B只有一个节点

CD分别一个子树，一个节点

E一个子树俩节点

特殊二叉树:完全、完美(满)、斜

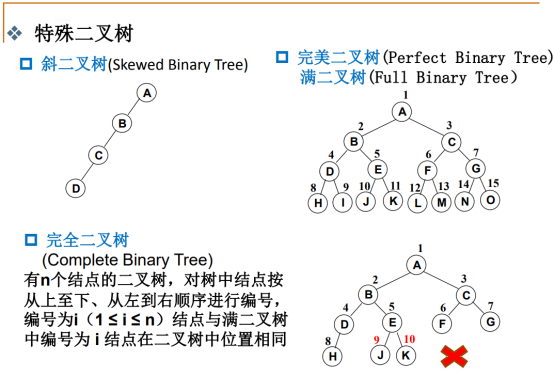
斜二叉树，往一边倒。左或右都行。

实际上是一个链表，形成一个线性结构了。

完美二叉树，每个结点都有两个儿子，除了最底下叶子结点的没有儿子，叶子结点都是比较齐整的，都在同一层。

完全二叉树不是满二叉树或者完美二叉树，但是允许缺掉最后几个结点，最下一层，右边可以少掉几个，左边还是齐整的。 完全二叉树是很重要的二叉树，很多数据结构就建立在完全二叉树基础之上 。

完全二叉树用数组实现非常方便，从上到下，从左到右， 结点和编号都是连续的 。

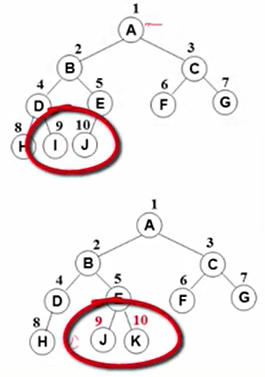
但图里的不是完全二叉树，左边缺了一个结点编号。

结点数

二叉树的层数，跟这一层的结点数量关系。

层次的计数是从1开始，是从根结点开始。

达到2的K次方-1的二叉树为完美二叉树。

(2的0次方+2的1次方+2的2次方+...+2的k-1次方=2的k次方-1)

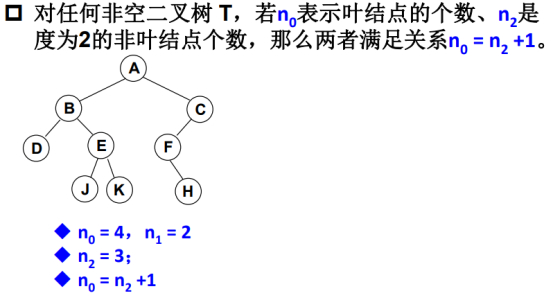
可以把二叉树的节点分成三种类型:

叶节点，没有儿子，即叶结点的总数n0个。

只有一个儿子的结点数n1个。

有两个儿子的结点数n2个。

二叉树总的结点数n=叶结点的总数n0+只有一个儿子的结点数n1+有两个儿子的结点数n2。

证明n0=n2+1。

从边的角度考虑这个问题，除了根结点没有边之外，每个结点往上看，有且仅有一条边，那么边的总数为总的结点数-1，即:总的边数=n0+n1+n2-1。

每个结点往下看，不同类型的结点，对往下边的贡献是不同的，n0结点没有儿子结点也没有边，贡献是0n0，没有边的贡献，n1结点只有一条边往下，对于边的贡献是1n1，n2结点往下/往上有两条边，对于边的贡献是2*n2。

那么n0+n1+n2-1 = 0n0 + 1n1 + 2*n2，最终约出来n0=n2+1。

抽象数据类型(构成)与遍历方法

从抽象数据类型角度来看， 最重要的操作是遍历 ，在二叉树中要求解很多问题，很多算法，就是建立在树的遍历基础上面。

遍历总得有个次序，二叉树由三块组成:根结点、左子树、右子树。

3.2.2 二叉树的存储结构

顺序存储结构:数组

首先可以思考，是否可以使用数组来表示二叉树？

二叉树，分支比较少。

前面学习的完全二叉树用数组实现非常方便，从上到下，从左到右， 结点和编号都是连续的 。

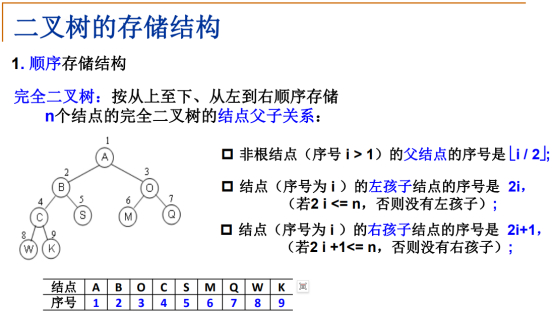
可以把编号跟数组下标对应起来，这样的话，就可以把完全二叉树放在数组中。

那么，通过已知结点需要找到对应的关系，父子关系。

父节点，取不超过(i/2)的最大整数 。

有规律可循，因为是顺序编号，所以左边是2i，右边是2i+1。

比如5S这个结点，2i=10超出了n=9结点总数，所以没有左子结点。

所以可以说，完全二叉树可以用数组来存储，不仅能够保持连续，也能找出父子关系。

但是缺结点的树，可以把它补充成一个完全二叉树，相应的缺点是，会在数组中留下一个空位。

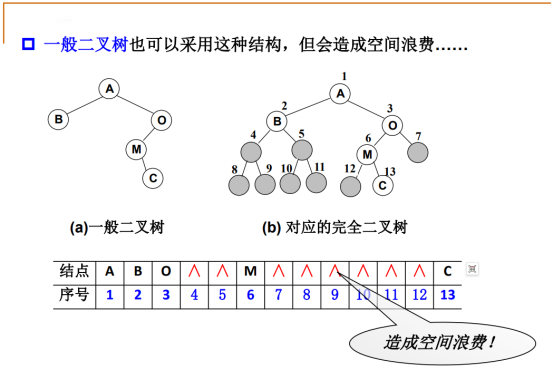
一般二叉树照着完全二叉树用数组存储，对应关系扔可存在，无结点的位置必须留着。

用一般二叉树和完全二叉树相比，会造成空间浪费。

顺序存储结构:链表

/*
二叉树的链表结构
*/
typedef struct TreeNode *BinTree;
//二叉树类型
typedef BinTree Position;
//树结点定义
struct TreeNode{
	//结点数据
	ElementType Data;
	//指向左子树
	BinTree Left;
	//指向右子树
	BinTree Right;
}

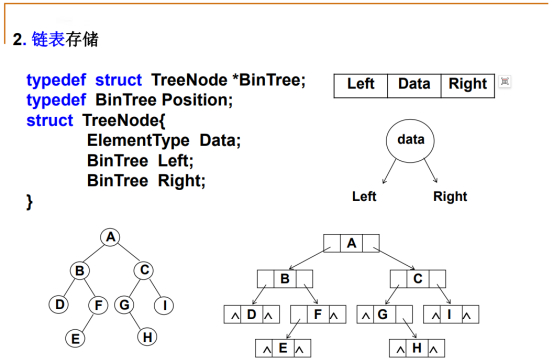
一般二叉树和完全二叉树都可以使用这种链表结构来表示，没结点的用NULL表示即可。