后面主要以链式存储为主来讲相应的遍历如何实现的。

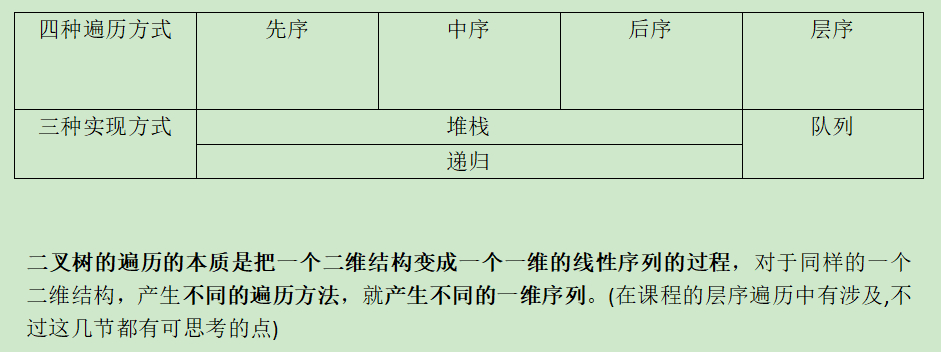
二叉树的遍历的本质是把一个二维结构变成一个一维的线性序列的过程 ，对于同样的一个二维结构，产生 不同的遍历方法 ，就 产生不同的一维序列 。(在课程的层序遍历中有涉及,不过这几节都有可思考的点)

3.3.1递归(堆栈实现)遍历

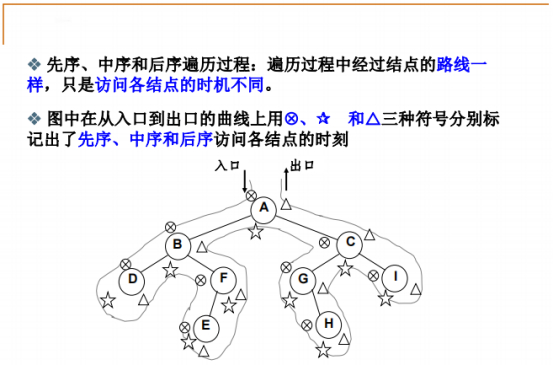
这里根据递归的原理来实现先序、中序、后序三种遍历方式，实际上递归是用堆栈来实现的。

先序遍历

/*
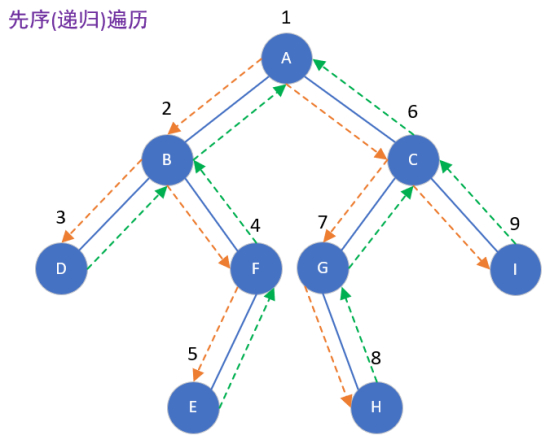
先序遍历
*/
void PreOrderTraversal(BinTree BT){
	/*
	BT是根结点的指针,也是左结点(左子树根结点的地址)
	进行递归。
	如果是空的,那么就直接退出。
	*/
	if(BT){
		//如果不空,那么先访问根结点。
		printf("%d",BT->Data);
		PreOrderTraversal(BT->Left);
		PreOrderTraversal(BT->Right);
	}
}

中序遍历

/*
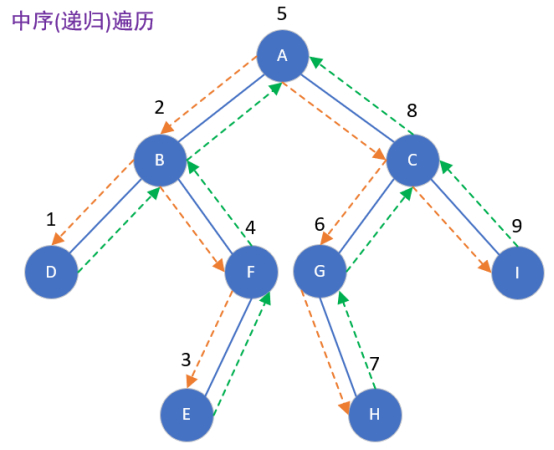
中序遍历
左根右
*/
void InOrderTraversal(BinTree BT){
	/*
	BT是根结点的指针,也是左结点(左子树根结点的地址)
	进行递归。
	如果是空的,那么就直接退出。
	*/
	if(BT){
		InOrderTraversal(BT->Left);
		printf("%d",BT->Data);
		InOrderTraversal(BT->Right);
	}
}

后序遍历

/*
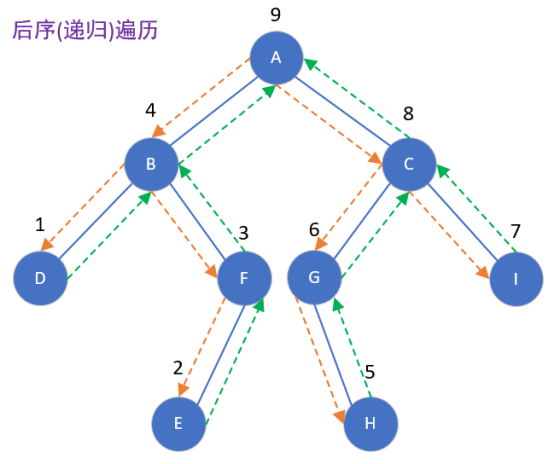
后序遍历
左右根
*/
void PostOrderTraversal(BinTree BT){
	/*
	BT是根结点的指针,也是左结点(左子树根结点的地址)
	进行递归。
	如果是空的,那么就直接退出。
	*/
	if(BT){
		PostOrderTraversal(BT->Left);
		PostOrderTraversal(BT->Right);
		printf("%d",BT->Data);
	}
}

3.3.2 非递归 (借助堆栈) 遍历

实际上递归是用堆栈来实现的。

这里借助堆栈(基本思路)把递归变成非递归来实现遍历循环算法。

中序遍历

/*
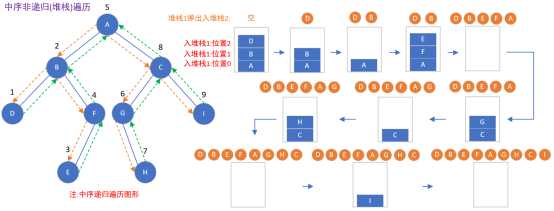
中序非递归(堆栈)遍历
左根右
*/
void InOrderTraversal2(BinTree BT){
	BinTree T = BT;
	//创建并初始化堆栈S
	Stack S = CreateStack(MaxSize);
	while(T || !IsEmpty(S)){
		/*
		一直向左并将沿途结点压入堆栈
		*/
		while(T){
			/*
			一、遇到一个结点,就把它压栈,并去遍历它的左子树。
			*/
			Push(S,T);
			T = T->Left;
		}
		if(!IsEmpty(S)){
			/*
			二、当左子树遍历结束(走到底)后，从栈顶弹出这个结点并访问它。
			*/
			T = Pop(S);
			printf("%5d",T->Data);
			/*
			三、按其右指针再去中序遍历该结点的右子树。(回到第一步)
			*/
			T = T->Right;
		}
	}
}

先序遍历

/*
先序非递归(堆栈)遍历
根左右
*/
void PreOrderTraversal2(BinTree BT){
	BinTree T = BT;
	//创建并初始化堆栈S
	Stack S = CreateStack(MaxSize);
	while(T || !IsEmpty(S)){
		/*
		一直向左并将沿途结点压入堆栈
		*/
		while(T){
			/*
			一、遇到一个结点,就把它压栈,并访问它,然后去遍历它的左子树。
			*/
			Push(S,T);
			printf("%5d",T->Data);
			T = T->Left;
		}
		if(!IsEmpty(S)){
			/*
			二、当左子树遍历结束(走到底)后,从栈顶弹出这个结点。
			*/
			T = Pop(S);
			/*
			三、按其右指针再去中序遍历该结点的右子树。(回到第一步)
			*/
			T = T->Right;
		}
	}
}

后序遍历(暂无源码)

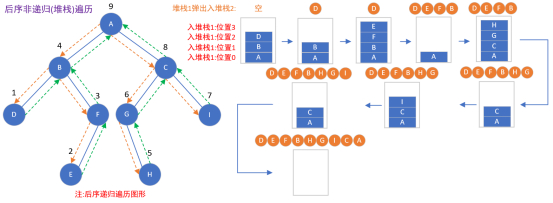
3.3.3 层序遍历

二叉树的遍历的本质是把一个二维结构变成一个一维的线性序列的过程，对于同样的一个二维结构，产生不同的遍历方法，就产生不同的一维序列。(在课程的层序遍历中有涉及,不过这几节都有可思考的点)

那么，如果不访问父节点，那么左右儿子是访问不到的。

当访问一个结点时，下一个结点可能是左儿子，也可能是右儿子，如果记不住自身的节点，那么反过来是访问不到原左右儿子结点的，回不到父节点。

如果访问了左儿子，右儿子怎么访问？

如果丢掉了右儿子，那么就永远再也找不到了右儿子了。

在二叉树遍历的核心问题中:要用一种方法把父节点、左右儿子结点都保存下来，方法有堆栈和队列。

特征:一层层访问、指针入队。

/*
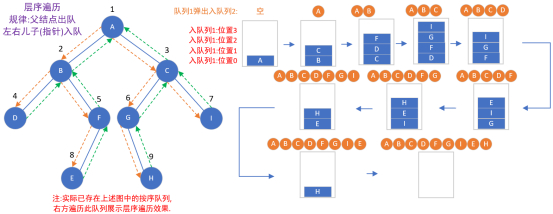
层序遍历
特征:一层层访问。
基本过程:先根结点入队,然后
1)从(已有)队列中取出一个元素。
2)访问该元素所指结点。
3)若该元素所指结点的左右孩子结点非空,则将其左右孩子的(指针)顺序入队。
*/
void LevelOrderTraversal2(BinTree BT){
	Queue Q;
	BinTree T;
	//若是空树,则直接返回.
	if(!BT){
		return;
	}
	//创建并初始化队列Q
	Q = CreateQueue(MaxSize);
	//实际上是有所有值的
	AddQ(Q,BT);
	//这里来一个个的遍历
	while(!IsEmpty(Q)){
		//删除原队列中的结点
		T = Delete(Q);
		//取出并访问
		printf("%d\n", T->Data);
		//输出此结点的左右儿子结点并把其指针添加到队列中
		if(T->Left){
			AddQ(Q, T->Left);
		}
		if(T->Right){
			AddQ(Q, T->Right);
		}
	}
}

3.3.4 遍历应用例子

输出二叉树叶子结点

/*
输出二叉树中的叶子结点
改造:先序递归遍历
*/
void PreOrderPrintLeaves(BinTree BT){
	/*
	BT是根结点的指针,也是左结点(左子树根结点的地址)
	进行递归。
	如果是空的,那么就直接退出。
	*/
	if(BT){
		//如果左右结点都没有儿子了,说明是叶子结点并输出.
		if(!BT->Left && !BT->Right){
			printf("%d",BT->Data);
		}
		//输出叶子结点
		else{
			PreOrderTraversal(BT->Left);
			PreOrderTraversal(BT->Right);
		}
	}
}

求二叉树高度

/*
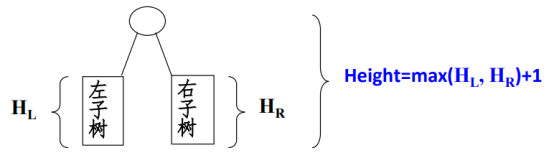
求二叉树的高度
左右两个子树的最大高度+1
*/
int PostOrderGetHeight(BinTree BT){
	int HL, HR, MaxH;
	if(BT){
		//求左子树的深度
		HL = PostOrderGetHeight(BT->Left);
		//求右子树的深度
		HR = PostOrderGetHeight(BT->Right);
		//求左右子树较大的深度
		MaxH = (HL > HR) ? HL : HR;
		//返回树的深度
		return (MaxH + 1);
	}else{
		return 0;
	}
}

二元运算表达式树及其遍历

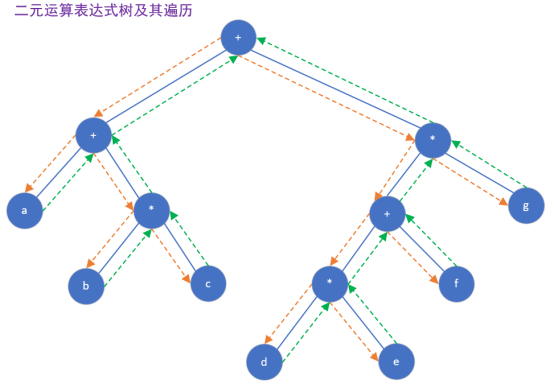
这里叶结点是运算数，非叶结点是运算符号。

三种遍历可以得到三种不同的访问结果:

先序遍历得到前缀表达式:++abc+*defg

中序遍历得到中缀表达式:a+bc+de+f*g

注:中缀表达式不准,因为会受到运算符优先级的影响，解决方法为输出左子树时加左右括号。

修改后为:(a+(bc))+(((de)+f)*g)

后序遍历得到后缀表达式:abc*+def+g+

由两种遍历序列确定二叉树

已知三种遍历中的任意两种遍历序列，不一定可以唯一确定一颗二叉树，必须其中有一个中序遍历才可以。

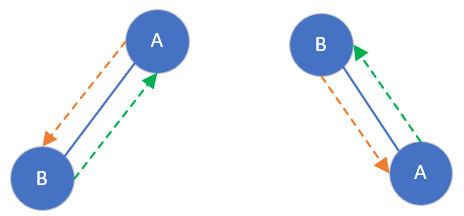
因为前序的顺序是”根左右”，而后序的顺序是”左右根”。

比如上图中的先序是:AB，后序是BA，并不能唯一的确定一颗二叉树。

中序和先序遍历序列来确定一颗二叉树

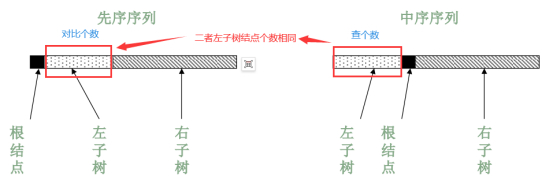
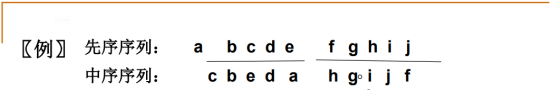
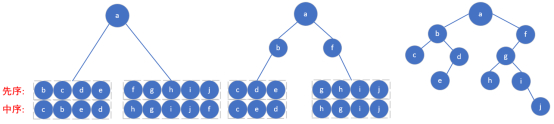
第一层到第二层结点，都是取先序的第一个结点，之后，要自己推算出来。

源码: 二叉树的四种遍历

void InorderTraversal( BinTree BT )
{
    if( BT ) {
        InorderTraversal( BT->Left );
        /* 此处假设对BT结点的访问就是打印数据 */
        printf("%d ", BT->Data); /* 假设数据为整型 */
        InorderTraversal( BT->Right );
    }
}

void PreorderTraversal( BinTree BT )
{
    if( BT ) {
        printf("%d ", BT->Data );
        PreorderTraversal( BT->Left );
        PreorderTraversal( BT->Right );
    }
}

void PostorderTraversal( BinTree BT )
{
    if( BT ) {
        PostorderTraversal( BT->Left );
        PostorderTraversal( BT->Right );
        printf("%d ", BT->Data);
    }
}

void LevelorderTraversal ( BinTree BT )
{ 
    Queue Q; 
    BinTree T;

    if ( !BT ) return; /* 若是空树则直接返回 */
  
    Q = CreatQueue(); /* 创建空队列Q */
    AddQ( Q, BT );
    while ( !IsEmpty(Q) ) {
        T = DeleteQ( Q );
        printf("%d ", T->Data); /* 访问取出队列的结点 */
        if ( T->Left )   AddQ( Q, T->Left );
        if ( T->Right )  AddQ( Q, T->Right );
    }
}

小总结