4.2.1 什么是平衡二叉树

介绍

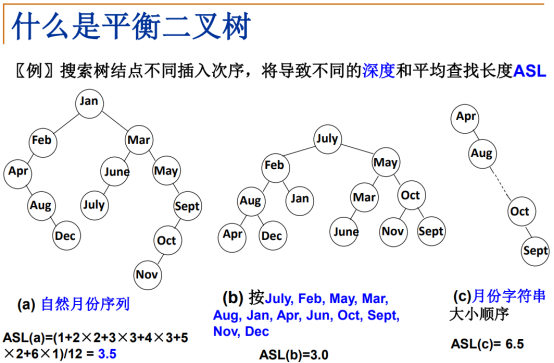
A按照自然月份排序。

比较1、2、3月份，分别要比较1、2、3次。这12个月份都要比较。

第三层有3个结点，第四层有3个结点。

这里指平均要花多少时间。平均成功的查找长度。

B按照现在的蓝色排序。

计算同A

C按照英文单词字典顺序。每次插入都比上一个结点要大。

最糟糕，Apr是1次，Sept是12次。

导致的问题，不同的插入顺序，就会形成不同的树结构，这样不同的搜索树，查找效率不同，一个衡量指标叫做平均查找长度。

可以发现，B查找长度最短，相对另外两个，这样的树结构比较好，总体感觉比较平衡，左右两边比较均匀。

一种树均匀的描述方法是两边结点一样，这个要求高，这里要求放低一些，两种指标来衡量:左右两边结点数差不多和左右两边高度差不多(差1)，这样认为是基本平衡，叫做平衡二叉树。

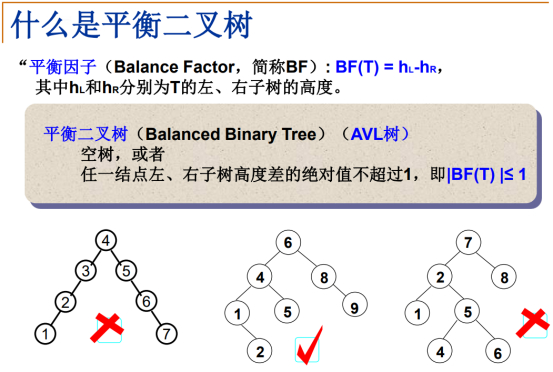
AVL是提出平衡二叉树的科学家以他们名字的首字母来命名的。

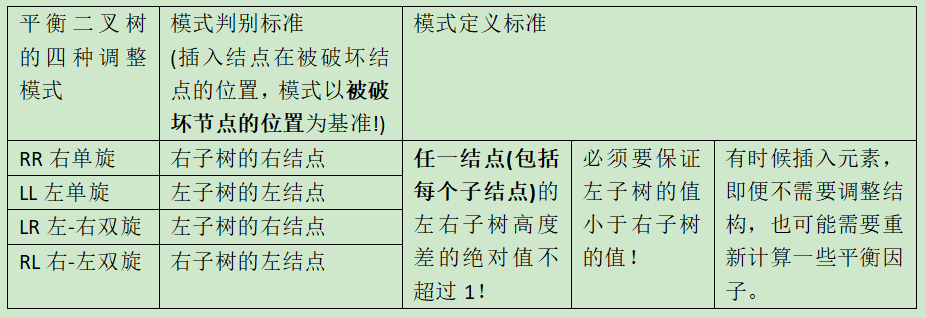
注意:这里强调的是 任一结点(包括每个子结点) 的左右子树高度差的绝对值不超过1！

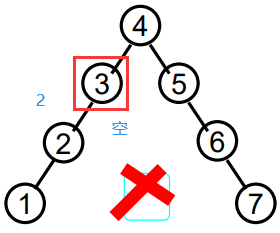
结点4:左右两边高度差等于0。

结点3:左边高度2，右边0，高度差2，超过了1。

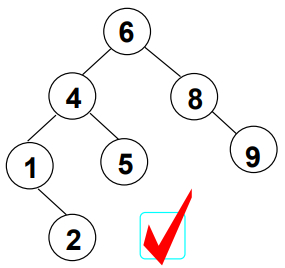
任何结点的左右子树的高度差绝对值最大为1。

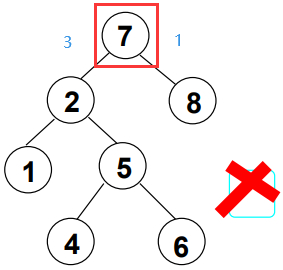
结点7:左边高度3，右边1，高度差2，超过了1。

AVL树高度与斐(fei)波那契序列

平衡的目的是让树的高度能够低一点，因为越平衡树的高度越低，越不平衡就会往一边倒，导致树的高度会越高。

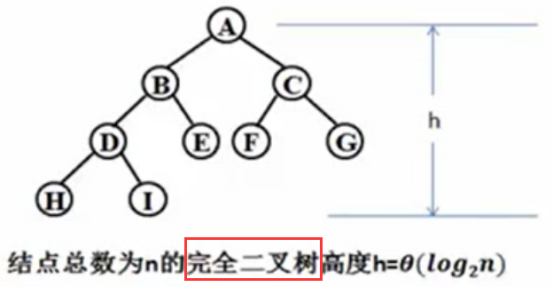
上述完全二叉树的高度能达到Log以2为底N的对数，那么平衡二叉树是否也能达到

O(Log以2为底N的对数)呢？

这里的高度是这个路径的一个长度，边的个数。

高度为0，1个结点。

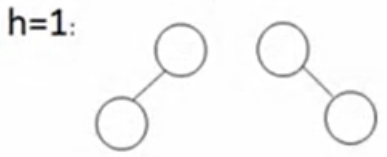
高度为1，最少要两个结点，两种情况:一种左右两边都有这个高度为1，另外一种，左边或右边缺一个。

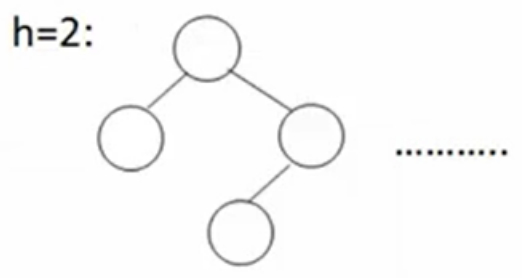
高度为2，至少需要3层，如拿调左边的结点，那么就不平衡，如拿调右边最下面的结点，高度就不为2。

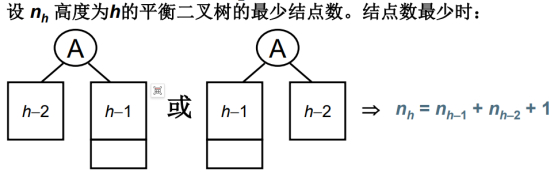
Nh = 高度N(h-1)时最少的结点数+高度N(h-2)时最少的结点数+1

上述两个不管哪种情况，总归是左儿子结点数+右儿子结点数。( 同3.2的计算方法 )

上述内容跟下述斐(fei)波那契序列很像，后面的数都是前面两个数的和。

唯一的差别是后面+1。

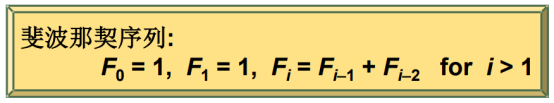
4.2.2 平衡二叉树的调整(左右子树高度绝对值相差1)

比如在对原来的一颗平衡二叉树，做插入删除操作时，变得不平衡了(变成-2或2了)，要找到发现者、破坏者和被破坏者(麻烦结点)，那么就要做平衡二叉树的调整。

要注意的是，平衡二叉树是一个搜索树或者查找树，后面所有的调整，一定要保证它仍然是一个搜索树或者查找树，而且要保证，左子树比根结点小，右子树比根结点大。

RR插入需要RR(Right Right Rotation)旋转(右单旋)

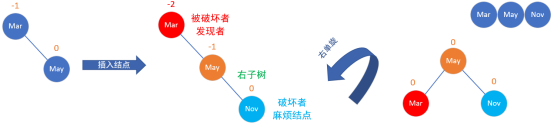
平衡被破坏的发现者/被破坏者结点:Mar

破坏者/麻烦结点:Nov

平衡被破坏的发现者/被破坏者结点与破坏者/麻烦结点的关系:破坏者/麻烦结点是在平衡被破坏的发现者/被破坏者结点的右子树的右子树上。

插入:RR插入(插入的结点插在某个结点的 右边/左边 )

旋转:RR旋转(可想象成高中物理的 右手定则 )

( 移动的是橘黄色节点，即:紧挨着破坏者节点的节点。 )

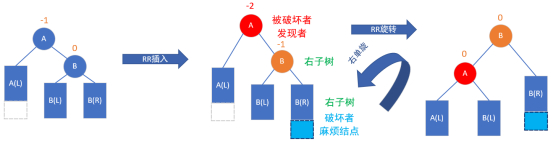
被破坏的结点跟插入的这个结点是右子树，在右子树上的插入，这个时候做RR旋转，就是把被破坏的右子树拎上来，左边的BL一定比A大，比B小，那么BL要挂在A的右边，B的左边，这样就变平衡了。

RR案例1:添加右子树

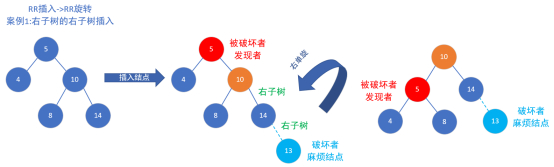
平衡被破坏的发现者/被破坏者结点:5

破坏者/麻烦结点:13

平衡被破坏的发现者/被破坏者结点与破坏者/麻烦结点的关系:破坏者/麻烦结点是在平衡被破坏的发现者/被破坏者结点的右子树的右子树上。

插入:RR插入(插入的结点插在某个结点的 右边/左边 )

旋转:RR旋转(可想象成高中物理的 右手定则 )

RR案例2:添加左子树

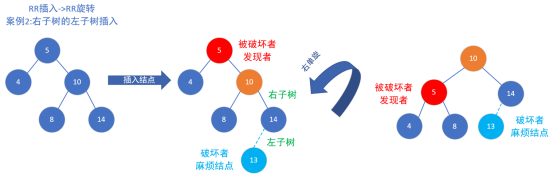
平衡被破坏的发现者/被破坏者结点:5

破坏者/麻烦结点:13

平衡被破坏的发现者/被破坏者结点与破坏者/麻烦结点的关系:破坏者/麻烦结点是在平衡被破坏的发现者/被破坏者结点的右子树的左子树上。

插入:RR插入(插入的结点插在某个结点的 右边/左边 )

旋转:RR旋转(可想象成高中物理的 右手定则 )

LL插入需要LL(Left Left Rotation)旋转(左单旋)

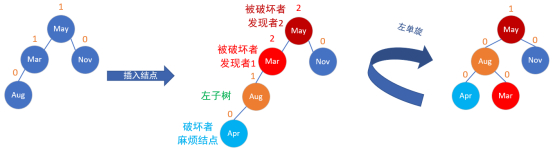
平衡被破坏的发现者/被破坏者结点:Mar

破坏者/麻烦结点:Apr

平衡被破坏的发现者/被破坏者结点与破坏者/麻烦结点的关系:破坏者/麻烦结点是在平衡被破坏的发现者/被破坏者结点的左子树的左子树上。

插入:LL插入(插入的结点插在某个结点的 右边/左边 )

旋转:LL旋转(可想象成高中物理的 左手定则 )

还要发现一个问题，由于Apr的插入，导致May结点的平衡性也被破坏了，此时，两个结点的平衡性都被破坏了，但是对于现在的调整来讲，只要下面的这样一点平衡了，上面的结点也就平衡了( 跟调试程序编译错误一样，第一个错误改了，后面的错误可能就没了 )。

( 移动的是橘黄色节点，即:紧挨着破坏者节点的节点。 )

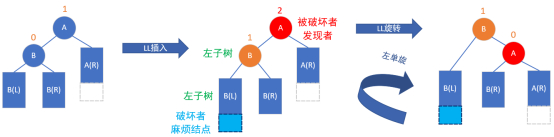
被破坏的结点跟插入的这个结点是左子树，在左子树上的插入，这个时候做LL旋转，就是把被破坏的左子树拎上来，左边的BR一定比B大，比A小，那么BR要挂在B的右边，A的左边，这样就变平衡了。

LR插入需要LR(Double Left Right Rotation)旋转(左-右双旋)

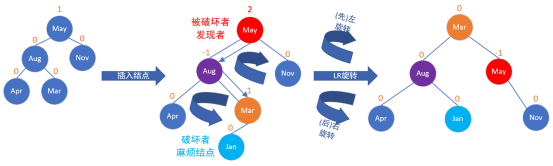
(注:在前面LL的图形基础上处理)

平衡被破坏的发现者/被破坏者结点:May

破坏者/麻烦结点:Jan

平衡被破坏的发现者/被破坏者结点与破坏者/麻烦结点的关系:破坏者/麻烦结点是在平衡被破坏的发现者/被破坏者结点的左子树的右子树上。

插入:LR插入(插入的结点插在某个结点的 右边/左边 )

旋转:LR旋转(可想象成高中物理的 (先)左手定则和(后)右手定则 )

( 移动的是橘黄色节点，即:紧挨着破坏者节点的节点。 )

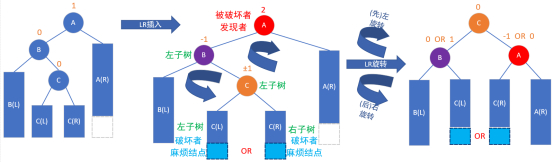
重点关注彩色颜色的圈。

插入的结点无论是插入左结点还是右结点，总归破坏了A的平衡性。

这里做左右旋转的基本模式就是把ABC转换成CBA，因为是平衡二叉/搜索树，所以一定要左边小，右边大，并满足平衡二叉/搜索树的条件。

注:这里的案例，LR和RL的结点是相对称的。

RL插入需要RL(Double Right Left Rotation)旋转(右-左双旋)

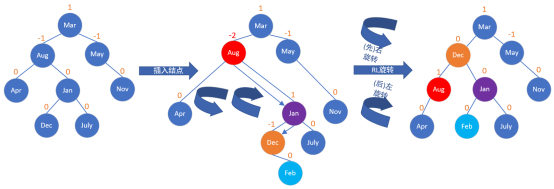
(注:在前面LR的图形基础上处理)

平衡被破坏的发现者/被破坏者结点:Aug

破坏者/麻烦结点:Feb

平衡被破坏的发现者/被破坏者结点与破坏者/麻烦结点的关系:破坏者/麻烦结点是在平衡被破坏的发现者/被破坏者结点的右子树的左子树上。

插入:RL插入(插入的结点插在某个结点的 右边/左边 )

旋转:RL旋转(可想象成高中物理的 (先)右手定则和(后)左手定则 )

( 移动的是橘黄色节点，即:紧挨着破坏者节点的节点。 )

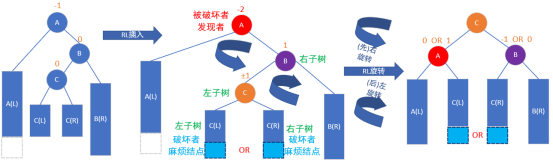
重点关注彩色颜色的圈。

插入的结点无论是插入左结点还是右结点，总归破坏了A的平衡性。

这里做左右旋转的基本模式就是把ABC转换成CBA，因为是平衡二叉/搜索树，所以一定要左边小，右边大，并满足平衡二叉/搜索树的条件。

注:这里的案例，LR和RL的结点是相对称的。

案例综合(重新计算平衡因子)

(注:在前面RL的图形基础上处理)

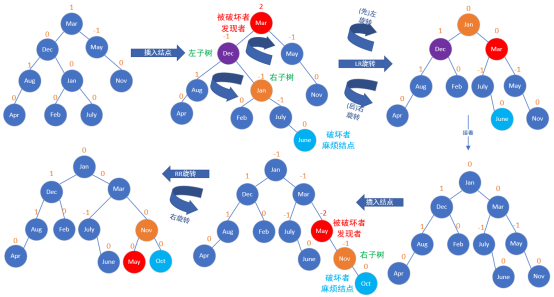
第一行

平衡被破坏的发现者/被破坏者结点:Mar

破坏者/麻烦结点:June

平衡被破坏的发现者/被破坏者结点与破坏者/麻烦结点的关系:破坏者/麻烦结点是在平衡被破坏的发现者/被破坏者结点的左子树的右子树上。

插入:LR插入(插入的结点插在某个结点的 右边/左边 )

旋转:LR旋转(可想象成高中物理的 (先)左手定则和(后)右手定则 )

第二行

平衡被破坏的发现者/被破坏者结点:May

破坏者/麻烦结点:Oct

平衡被破坏的发现者/被破坏者结点与破坏者/麻烦结点的关系:破坏者/麻烦结点是在平衡被破坏的发现者/被破坏者结点的右子树的右子树上。

插入:RR插入(插入的结点插在某个结点的 右边/左边 )

旋转:RR旋转(可想象成高中物理的 右手定则 )

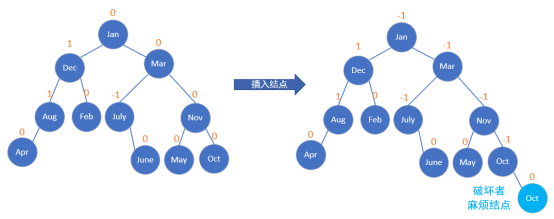
此节点插入时，平衡二叉树依旧是平衡二叉树，左图中右边的平衡因子都是0，插入之后，平衡因子都变成了-1。

所以说，当插入结点不影响平衡二叉树的平衡性时，树结构是不变的，但是平衡因子还是会改变的。

4.2.3平衡二叉树的旋转与插入(源码)

#include<stdio.h>
int main(void){
	return 0;
}
/*
平衡二叉树AVL的旋转与插入
*/
typedef struct AVLNode *Position;
//AVL树类型
typedef Position AVLTree;
struct AVLNode{
	//结点数据
	ElementType Data;
	//指向左子树
	AVLTree Left;
	//指向右子树
	AVLTree Right;
	//树高度
	int Height;
}
int Max(int a, int b){
	return a > b ? a : b;
}
/*
左单旋
LL旋转
*/
AVLTree SingleLeftRotation(AVLTree A){
	/*
	A必须有一个左子节点B
	将A与B做左单旋,更新A与B的高度,返回新的根结点B.
	*/
	AVLTree B = A->Left;
	A->Left = B->Right;
	B->Right = A;
	A->Height = Max(GetHeight(A->Left), GetHeight(A->Right)) + 1;
	B->Height = Max(GetHeight(B->Left), A->Left) + 1;
	return B;
}
/*
左-右双旋
LR双转
*/
AVLTree DoubleLeftRightRotation(AVLTree A){
	/*
	注意:A必须有一个左子节点B,且B必须有一个右子结点C
	将A、B与C做两次单旋,返回新的根结点C
	*/
	/*
	将B与C做右单旋,C被返回
	*/
	A->Left = SingleRightRotation(A->Left);
	/*
	将A与C做左单旋,C被返回.
	*/
	return SingleLeftRotation(A);
}

/*
右单旋
RR旋转
*/
AVLTree SingleRightRotation(AVLTree A){

}

/*
右-左双旋
RL双转
*/
AVLTree DoubleRightLeftRotation(AVLTree A){

}

/*
将X插入AVL树T中,并且返回调整后的AVL树.
*/
AVLTree Insert(AVLTree T, ElementType X){
	/*
	若插入空树,则新建包含一个结点的树.
	*/
	if(!T){
		T = (AVLTree)malloc(sizeof(struct AVLNode));
		T->Data = X;
		T->Height = 0;
		T->Left = T->Right = NULL;
	}
	/*
	插入T的左子树
	*/
	else if(X < T->Data){
		T->Left = Insert(T->Left, X);
		//如果需要左旋
		if(GetHeight(T->Left) - GetHeight(T->Right) == 2){
			if(X < T->Left->Data){
				//左单旋
				T = SingleLeftRotation(T);
			}
			else{
				//左-右双旋
				T = DoubleLeftRightRotation(T);
			}
		}
	}
	/*
	插入T的右子树
	*/
	else if(X > T->Data){
		T->Right = Insert(T->Right, X);
		//如果需要右旋
		if(GetHeight(T->Left) - GetHeight(T->Right) == -2){
			if(X > T->Right->Data){
				//右单旋
				T = SingleRightRotation(T);
			}
			else{
				//右-左双旋
				T = DoubleRightLeftRotation(T);
			}
		}	
	}
	/*
	插入右子树结束
	else if
	*/
	/*
	无需插入
	else X == T->Data
	*/
	/*
	别忘了更新树高
	*/
	T->Height = Max(GetHeight(T->Left), GetHeight(T->Right)) + 1;

	return T;

}

小总结