4.1.1 二叉搜索树及查找

静态查找:对象集合元素主要做find操作，元素不动。

动态查找:对象集合元素本身会动态的变化，除了查找外，还有插入删除操作发生。

一个很好的二分查找方法:把一般的顺序查找的时间复杂性从LogN降到了Log2N，二分查找效率好的重要原因就是把查找的数据事先进行的有效组织，这样给定了N个数，查找的顺序可以形成判定树结构，所以把一个线性的查找过程类似树上的一个查找过程，查找效率类似于树的高度。

得到启示:有没有可能把元素放在树上，而不是数组里面，放在树上，动态性比较高，插入删除操作比在线性中处理要方便，这就是二叉搜索/查找树。

在判定树中，有无可能说树上的任何一个结点，它的值比所有树的左子树的值都大，比右子树都小，这样查找过程就变成了对当前结点的判断，查找范围缩小了一大半。

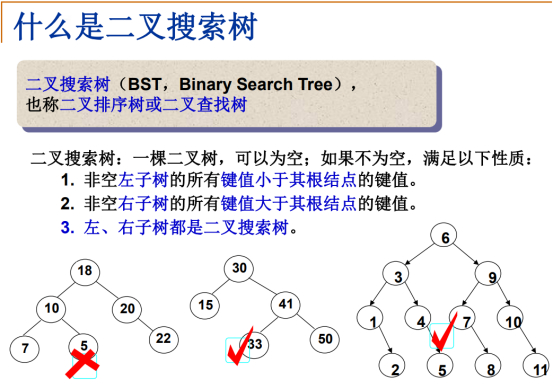
第一个图中的5这个位置的值应该比10大才对。

/*
二叉搜索树的查找操作FIND
尾递归
递归实现的效率并不是很高.
尾递归在分支的最后程序要返回的时候再出现递归,
从遍历的角度来讲,尾递归可以用循环来实现.
*/
Position Find(ElementType X, BinTree BST){
	if(!BST){
		//查找失败
		return NULL;
	}
	if(X > BST->Data){
		//在右子树中继续查找,那么右子树的根就是right
		return Find(X, BST->Right);
	}
	else if(X < BST->Data){
		//在左子树中继续查找,那么左子树的根就是left
		return Find(X, BST->Left);
	}
	else{
		/*
		X == BST->Data
		查找成功,返回结点的找到结点的地址.
		*/
		return BST;
	}
}

/*
二叉搜索树的查找操作IterFind
由于非递归函数的执行效率高,可将"尾递归"函数改为这里的"迭代"函数.
查找的效率取决于树的高度.
*/
Position IterFind(ElementType X, BinTree BST){
	while(BST){
		if(X > BST->Data){
			//向右子树中移动,继续查找.
			BST = BST->Right;
		}
		else if(X < BST->Data){
			//向左子树中移动,继续查找.
			BST = BST->Left;
		}
		else{
			//X == BST->Data
			//查找成功,返回结点并找到结点的地址.
			return BST;
		}
	}
	//查找失败
	return NULL;
}

而对同样的N个结点来讲，树的高度是和树的结构有关的，如果树的结构不合理，比如都只有左儿子没有右儿子全串在一起，形成一条链，往左边倾斜，高度是N-1，这是最坏的情况，右边同理。

这样就达不到Log2N，那么我们希望这个树看起来比较平衡，不往一边倒，就是后面要说的平衡二叉树。

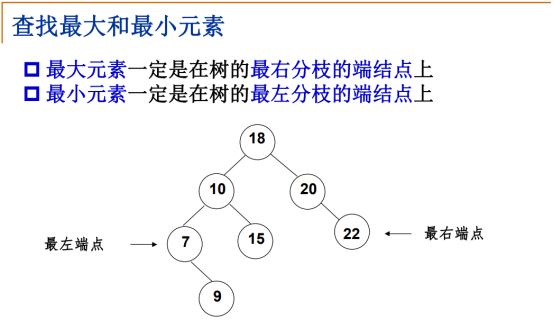
最大查找(找最大值)和最小查找(找最小值)。

查找树的特点:根结点开始一直往左走，走到底就是最小值，往右边走，走到底就是最大值。

/*
二叉搜索树的查找操作FindMin
查找最小元素的递归函数
尾递归
左边空了,意味着是这个树的最左边.
*/
Position FindMin(BinTree BST){
	if(!BST){
		//查找失败
		return NULL;
	}
	if(!BST->Left){
		//找到最左叶子结点并返回
		return BST;
	}
	else{
		//沿着左子树分支继续查找
		return FindMin(X, BST->Left);
	}
}

/*
二叉搜索树的查找操作IterFind
查找最大元素的迭代函数.
查找的效率取决于树的高度.
*/
Position FindMax(BinTree BST){
	if(BST){
		while(BST->Right){
			BST = BST->Right;
		}
	}
	return BST;
}

4.1.2 二叉搜索树的插入

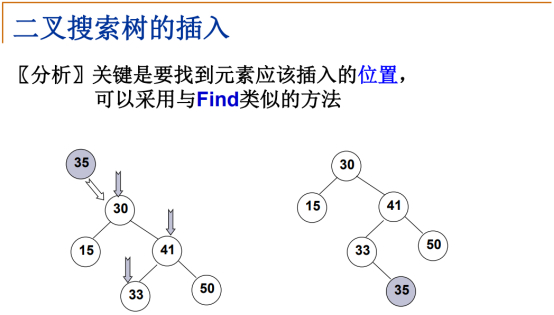
要保证插/删完新的结点之后，这个树还是二叉搜索树。

依然要保证，左子树的结点要比根结点小，右子树的结点要比根结点大。

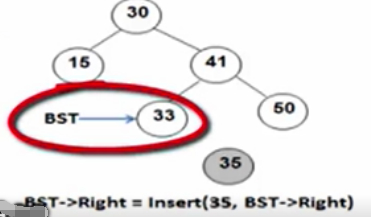
比如35这个结点，判断到了33，此时33的右指针是NULL，35在插入这个位置时，必须记住33这个位置，调用递归，在此位置插入，这样，右子树就不是空的了。

/*
二叉搜索树的插入算法
*/
BinTree Insert(ElementType X, BinTree BST){
	if(!BST){
		//若原树为空,生成并返回一个结点的二叉搜索树.
		BST = malloc(sizeof(struct TreeNode));
		BST->Data = X;
		BST->Left = BST->Right = NULL;
	}
	else{
		//开始找要插入元素的位置
		if(X < BST->Data){
			//递归插入左子树
			//如果这里直接改成"return Insert(X, BST->Left);"就变成跟查找很像了.
			BST->Left = Insert(X, BST->Left);
		}
		//
		else if(X > BST->Data){
			//递归插入右子树
			//如果这里直接改成"return Insert(X, BST->Right);"就变成跟查找很像了.
			BST->Right = Insert(X, BST->Right);
		}
		//else X已经存在,什么都不做
	}
	return BST;
}

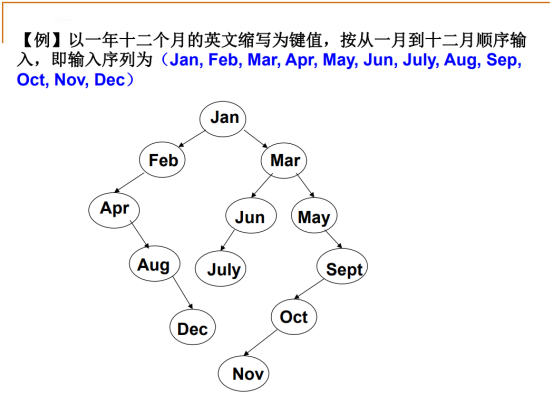
按照英文字典顺序，前面小，后面大。

4.1.3 二叉搜索树的删除

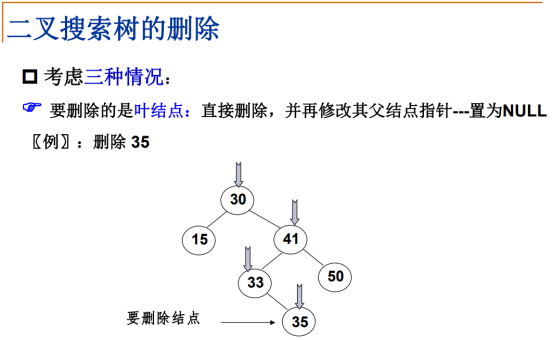
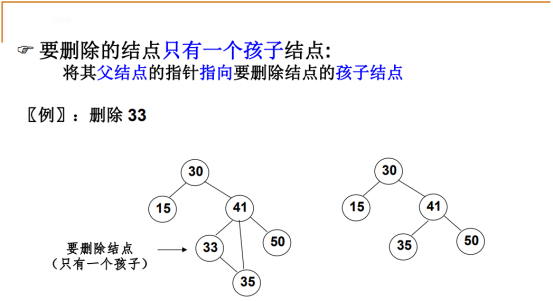
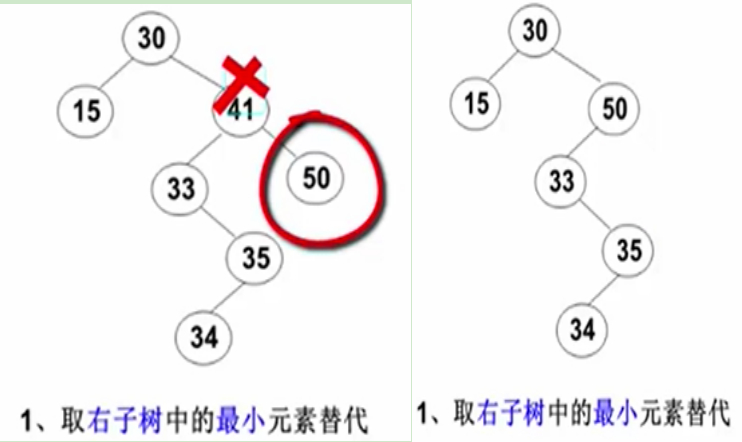
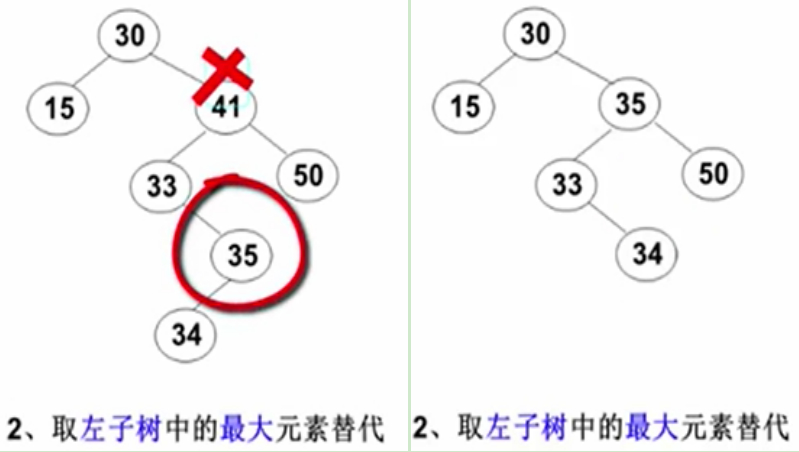
那比较复杂的是左右两边都不空，好处就是:

左子树的最大值一定是在左子树的最右边，有左儿子但不会有右儿子;

右子树的最小值一定在右子树的最左边，没有左儿子只有右儿子。

所以把这个删除的过程，变成是左右两边找最小或者最大的过程，使得要删除一个结点，有两个儿子结点的就变成上述图中的情况，要么没儿子，要么只有一个儿子的情况。

/*
二叉搜索树的删除
*/
BinTree Delete(ElementType X, BinTree BST){
	Position tmp;
	if(!BST){
		printf("要删除的元素未找到!");
	}
	else if(X < BST->Data){
		//左子树递归删除
		//返回新的左子树根结点的地址
		BST->Left = Delete(X, BST->Left);
	}
	else if(X > BST->Data){
		//右子树递归删除
		//返回新的右子树根结点的地址
		BST->Right = Delete(X, BST->Right);
	}
	//找到要删除的结点
	else{
		//一、被删除结点有左右两个子结点(都不为空的情况)
		if(BST->Left && BST->Right){
			tmp = FindMin(BST->Right);
			//在右子树中找最小的元素填充删除结点
			BST->Data = Tmp->Data;
			//在删除结点的右子树中删除最小元素
			BST->Right = Delete(BST->Data, BST->Right);
		}
		//二、被删除结点有一个或无子结点
		//儿子中有一个空或两个都是空的
		else{
			Tmp = BST;
			//2.1如果左结点为空,那么就把右节点接到父结点上去.
			if(!BST->Left){
				//有右孩子或无子结点
				BST = BST->Right;
			}
			//2.2如果右结点为空,那么就把左节点接到父结点上去.
			else if(!BST->Right){
				//有左孩子或无子结点
				BST = BST->Left;
			}
			free(Tmp);
		}
	}
	return BST;
}

源码: 二叉搜索树的插入与删除

BinTree Insert( BinTree BST, ElementType X )
{
    if( !BST ){ /* 若原树为空，生成并返回一个结点的二叉搜索树 */
        BST = (BinTree)malloc(sizeof(struct TNode));
        BST->Data = X;
        BST->Left = BST->Right = NULL;
    }
    else { /* 开始找要插入元素的位置 */
        if( X < BST->Data )
            BST->Left = Insert( BST->Left, X );   /*递归插入左子树*/
        else  if( X > BST->Data )
            BST->Right = Insert( BST->Right, X ); /*递归插入右子树*/
        /* else X已经存在，什么都不做 */
    }
    return BST;
}

BinTree Delete( BinTree BST, ElementType X ) 
{ 
    Position Tmp; 

    if( !BST ) 
        printf("要删除的元素未找到"); 
    else {
        if( X < BST->Data ) 
            BST->Left = Delete( BST->Left, X );   /* 从左子树递归删除 */
        else if( X > BST->Data ) 
            BST->Right = Delete( BST->Right, X ); /* 从右子树递归删除 */
        else { /* BST就是要删除的结点 */
            /* 如果被删除结点有左右两个子结点 */ 
            if( BST->Left && BST->Right ) {
                /* 从右子树中找最小的元素填充删除结点 */
                Tmp = FindMin( BST->Right );
                BST->Data = Tmp->Data;
                /* 从右子树中删除最小元素 */
                BST->Right = Delete( BST->Right, BST->Data );
            }
            else { /* 被删除结点有一个或无子结点 */
                Tmp = BST; 
                if( !BST->Left )       /* 只有右孩子或无子结点 */
                    BST = BST->Right; 
                else                   /* 只有左孩子 */
                    BST = BST->Left;
                free( Tmp );
            }
        }
    }
    return BST;
}