5.1.1 什么是堆 (存储、优先队列的完全二叉树:最大堆、最小堆)

堆，并不完全按照时间的先后顺序来进行排队，有时，需要考虑优先的级别。

数组:最简单的方法，不用排序，删除需要移动元素。

链表的结点拿掉要比数组简单，数组拿掉要挪位置，而链表直接改指针即可。

从头到尾找合适的位置，后面的元素要往后挪动。

从头到尾找合适的位置，修改指针。

树存储首先想到搜索树，插入和删除是跟树的高度有关，比如Log2N。

如果每次都想删除最大的，意味着每次都要删除最右边的，左边的不动，那么树就歪掉了，这样树的高度就不是Log2N了。

要重点考虑删除，因为比插入更难。

可以使用完全二叉树，把最大的放在每棵树的根节点，而且根据完全二叉树的左小右大特性，就可以满足现阶段删除的需求。

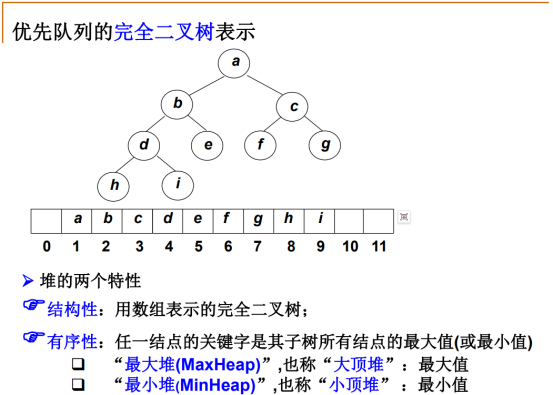
可以把元素放在数组中，从根节点下标为1的地方开始，逐步地往后面存放。

最大堆和最小堆，它们的结点都是有序的，从根结点到任意结点，所画路径到任意结点，由于有序性，使得后续的插入和删除操作，都是沿着这个有序的轨迹来完成。

即:要注意，跟结点到任意结点路径上结点序列的有序性!

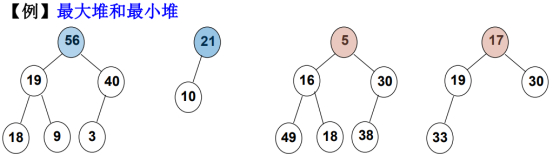
都是完全二叉树。

前2个:每棵树的根节点都比子结点大，最大堆。

后2个:每棵树的根节点都比子结点小，最小堆。

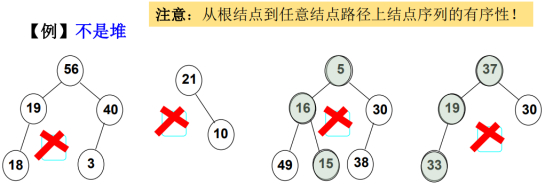
第1个:任何结点的值都是这个树里最大的，而且不是完全二叉树，左下角缺少右结点，不是最大堆。

第2个:不是完全二叉树，缺左结点。

第3个:是完全二叉树，可不能分辨是最大堆还是最小堆。

第4个:左下角缺少右结点，不是完全二叉树，且不能分辨是最大堆还是最小堆。

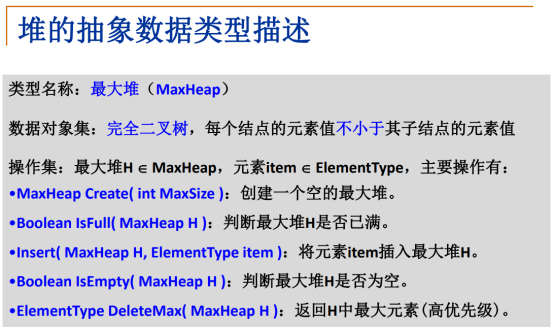
最主要的分别是插入和删除操作。

/*
最大堆的操作
*/
typedef struct HeapStruct *MaxHeap;
struct HeapStruct{
	//存储堆元素的数组
	ElementType *Elements;
	//堆的当前元素的个数
	int Size;
	//堆的最大容量(指示数组的大小)
	int Capacity;
};
/*
最大堆的创建
创建容量为MaxSize的空的最大堆
*/
MaxHeap Create(int MaxSize){
	MaxHeap H = malloc(sizeof(struct HeapStruct));
	/*
	申请数组空间大小
	MaxSize + 1:堆的正式元素是从下标为1的地方开始存放,下标为0的地方不存放堆的正式元素.
	*/
	H->Elements = malloc((MaxSize + 1) * sizeof(ElementType));
	H->Size = 0;
	H->Capacity = MaxSize;
	/*
	下标为0的地方,定义"哨兵",便于以后快速操作:
	定义为大于堆中所有可能元素的值MaxData,适用于创建最大堆.
	定义为小于堆中所有可能元素的值MinData,适用于创建最小堆.
	*/
	H->Elements[0] = MaxData;
}
bool IsFull( MaxHeap H ){
    return (H->Size == H->Capacity);
}

bool IsEmpty( MaxHeap H ){
    return (H->Size == 0);
}

5.1.2 (最大) 堆的插入(Log2N)

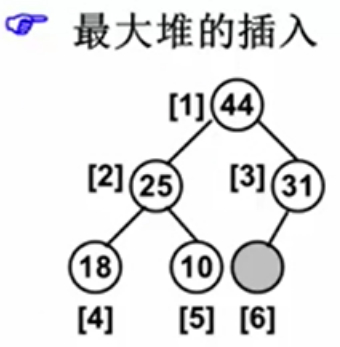
依然把堆看成是完全二叉树。

这里案例数据依然从数组下标1开始存放到5。

下述所有元素插入都是从此图开始处理。

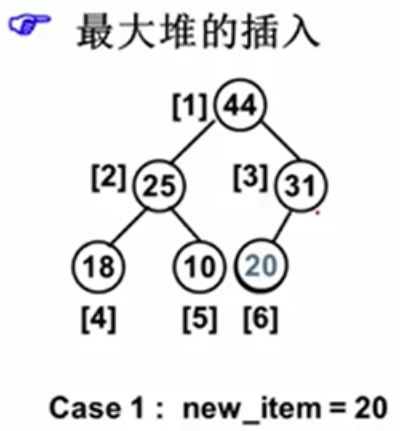
插入20,20没有破坏性。

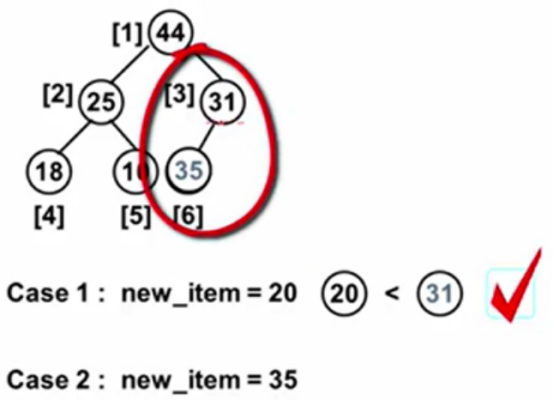
插入35，35破坏了有序性，所在子树根结点为31<35。

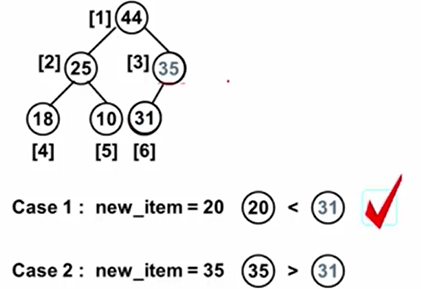
当35和31交换位置后就满足完全二叉树，最大堆。

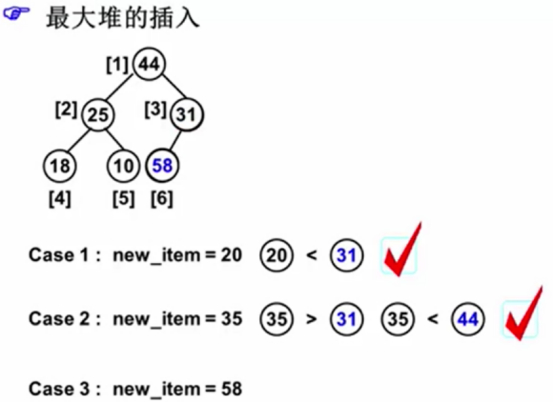
插入58，58破坏了有序性，所在子树根结点为31<58。

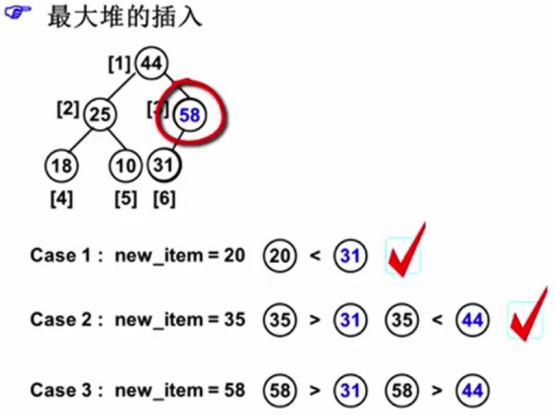
那么58和31交换位置，依旧不满足最大堆。

最后，58和44换位置，就可以满足最大堆。

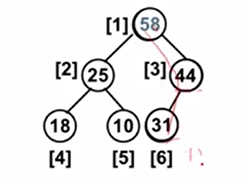
小总结:原来这条线是从根节点开始递降的，当往这个末尾插入某个元素之后，递降性质就变了，那么就需要父结点一直去调整，保证插入元素后，依然是有序的树，最终达到这个完全二叉树的最大堆效果。

/*
最大堆的插入
将新增结点插入到从其父结点到根结点的有序序列中
*/
void Insert(MaxHeap H, ElementType item){
	int i;
	if(IsNull(H)){
		printf("最大堆已满");
		return;
	}
	/*
	i指向插入后堆中最后一个元素的位置
	堆不满,就把这个元素放在堆的后面size+1的位置
	*/
	i = ++H->Size;
	/*
	i用来当前准备要放进去的位置,i/2是父结点,每次跟新增结点item元素比较
	如果item大于父结点,那么i = i/2,把父结点挪下来.
	在此循环中要记住:H->Elements[0]是哨兵元素,它大于堆中的最大元素,用于处理循环结束操作.
	循环解释(哨兵的作用):如果比较到数组第一个位置,还要继续往前就是位置0了,
	但这已经在堆外面了,应该还要再加一个条件i>1,等于1就不再做了
	为什么不加i>1呢?因为在数组下标为0的位置放置了比所有值都大的值MaxData哨兵,
	不用判断i>1也能使程序效率得到提升.
	*/
	for( ; H->Elements[i/2] < item; i/=2 ){
		/*
		向下过滤结点,把父结点挪下来.
		这里比交换数据的方式要快.
		*/
		H->Elements[i] = H->Elements[i/2];
	}
	/*
	将item插入最大堆H,其中H->Elements[0]已经定义为哨兵.
	*/
	H->Elements[i] = item;
}

这里插入结点的时间复杂度就是树的高度。

上述Insert程序的FOR循环解释:

比如这里插入25，会从树下往上一直和这个树中的结点比较，比较到数组下标1位置20就停下来了，数组下标0位置的值是哨兵设置的最大值1000。

/*
循环解释(哨兵的作用):如果比较到数组第一个位置,还要继续往前就是位置0了,
但这已经在堆外面了,应该还要再加一个条件i>1,等于1就不再做了
为什么不加i>1呢?因为在数组下标为0的位置放置了比所有值都大的值MaxData哨兵,
不用判断i>1也能使程序效率得到提升.
*/
for( ; H->Elements[i/2] < item; i/=2 ){
	/*
	向下过滤结点,把父结点挪下来.
	这里比交换数据的方式要快.
	*/
	H->Elements[i] = H->Elements[i/2];
}

5.1.3 (最大)堆的删除(Log2N)

最大堆删除，删除的位置是确定的根结点。

删除栈顶元素，左右子树都是堆。

元素删除的话，要把最后一个元素替换到这个栈顶的位置上，替换的时候发现，在堆删除的一个核心操作是，把下面左右堆的所有儿子中去比较，然后一个个调上来，这种思路，要注意删除元素时，也要把这个树调成一个完全二叉树堆的形式。

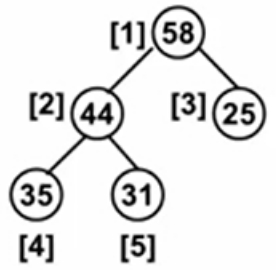
原树结构如上。

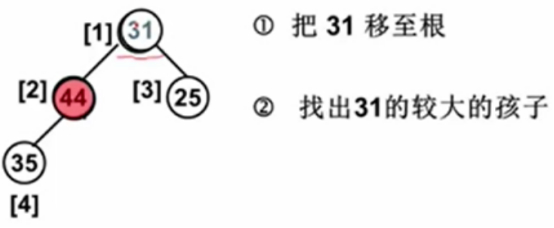
删除根结点58，用31替换。

树结构特性是保留了，但有序特性被破坏了。

31和44比较，换位置。

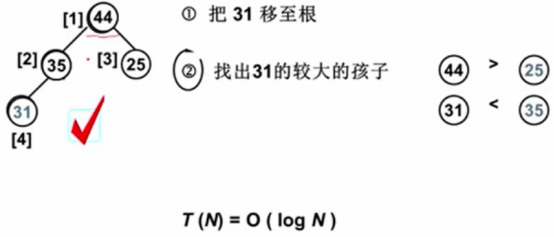
31和35比较，换位置。

现在又是完全二叉树，有序性又得到保证。所以移去的是数组位置5的结点。

这是删除的基本策略，时间复杂度就等于树的高度。

/*
从最大堆H中去除键值为最大的元素,并删除一个结点.
*/
ElementType DeleteMax(MaxHeap H){
	int Parent, Child;
	ElementType MaxItem, temp;
	if(IsEmpty(H)){
		printf("最大堆已空");
		return;
	}
	/*
	取出根结点存放的最大值.
	树根MaxItem是要删除的元素,要return回去.
	*/
	MaxItem = H->Elements[1];
	/*
	用最大堆中最后一个元素,从根节点开始向上过滤下层结点.
	删掉的元素拷贝到temp中.
	注意当前堆的规模要减小.
	*/
	temp = H->Elements[H->Size--];
	/*
	FOR循环目的是给temp找一个位置.
	初始Parent=1,看是否有左右儿子,是否有的条件Parent*2,
	从上述中找到一个大的.
	在完全二叉树中,i代表一个结点,左儿子2i,右儿子2i+1,
	如果左儿子2i已经超出了Size的范围,意味着左儿子已经在堆外面了,
	说明没左儿子,没左儿子肯定也没右儿子,循环退出,parent就是当前的位置,temp就被放出去了.
	----
	接下来目标是要在左右结点找一个大的元素,然后跟parent这个位置元素作比较,
	如何找大的呢,先假定左儿子大,所以有"Child=Parent*2",所以Child指向左儿子.
	child如果指向左儿子,右儿子是child+1,因为左儿子是2i,右儿子是2i+1.
	*/
	for(Parent = 1; Parent * 2 <= H->Size; Parent = Child){
		/*
		把结点往下挪"Parent=Child",继续跑到左右儿子中大的位置,继续比较.
		*/
		Child = Parent * 2;
		/*
		上下内容的根本目的:把child变量指向左右儿子里面最大的,
		child一开始设为左儿子,然后发现右儿子比我大,那么"Child++",
		如果右儿子不比我大,那么child还是左儿子.
		(Child == H->Size)有左儿子,是最后一个元素,没右儿子.
		(Child != H->Size)有右儿子.
		*/
		if((Child != H->Size) && 
			/*
			Child指向左右子结点的较大者
			如果右儿子比左儿子大,所以儿子里面大的在右儿子,所以"Child++".
			是不是比左右儿子中大的还要大.
			*/
			(H->Elements[Child] < H->Elements[Child + 1])){
				/* Child指向左右子结点的较大者 */
				Child++;
		}
		/*
		不再需要调整
		*/
		if(temp >= H->Elements[Child]){
			break;
		}else{
			/*
			移动temp元素到下一层.
			把左右儿子中最大的元素拷贝到此Parent位置中.
			*/
			H->Elements[Parent] = H->Elements[Child];
		}
	}
	/*
	找到要换的位置,最后一个元素来替代根这个位置.
	*/
	H->Elements[Parent] = temp;
	/*
	删除的结点要return出去
	*/
	return MaxItem;
}

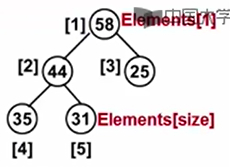
MaxItem = H->Elements[1];指向位置1。

temp = H->Elements[H->Size--];指向位置5。

5.1.4 (最大) 堆的建立 (堆排序、完全二叉树)

在排序里面可以用堆排序来做，首先要形成一个堆，这是建立堆应用的前提。

方法1:

做N轮循环，每次插入的时间复杂度是Log2N，总共循环N遍，所以整个时间复杂度是NLog2N，其实这个方法的效率不够。

方法2:

在O(N)时间内建立一个堆。分上述方法2中的两步。

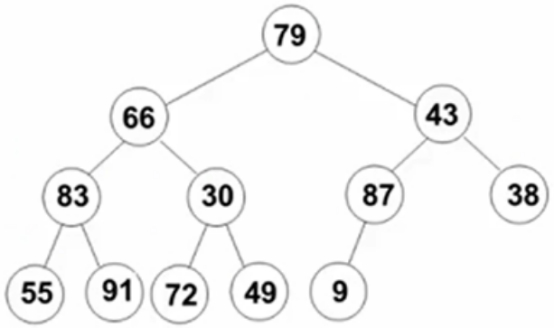
此12个元素在数组中顺序存放，从下标为1的位置N个数顺序存放，形成一颗完全二叉树。

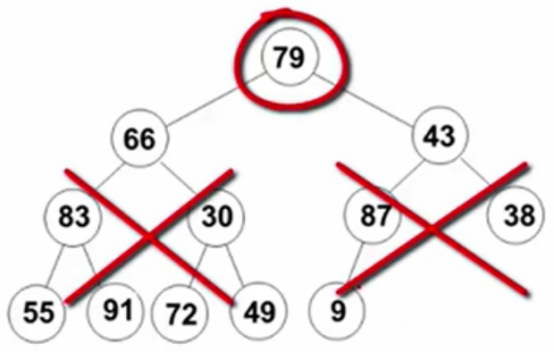
对79来讲，左右两边都不是堆，对66和43来讲，左右两边也都不是堆。

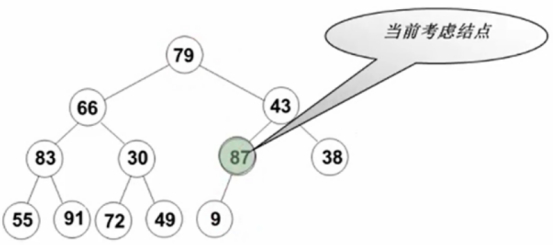
从倒数第一个有儿子的结点开始调整。

对这个结点来讲，因为第一个有儿子的结点，左边一定只有一个儿子，如果有右儿子的话，也只有一个儿子，也就左右最多只有一个儿子。

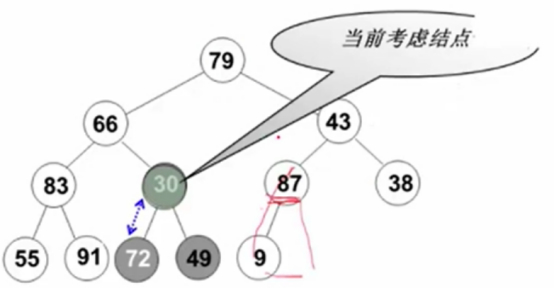
调30，72上去。

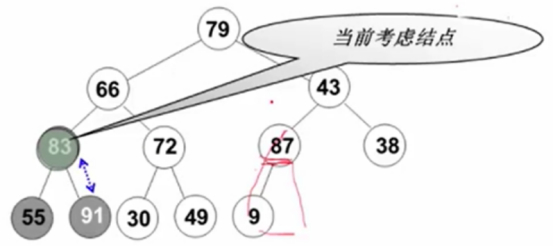
调83，91上去.

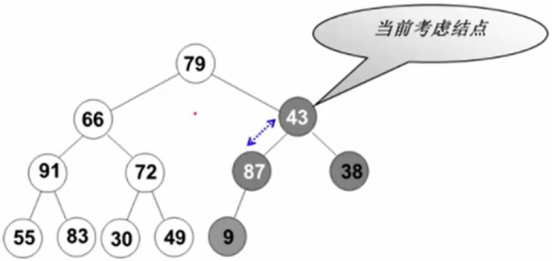
调43，87上去.

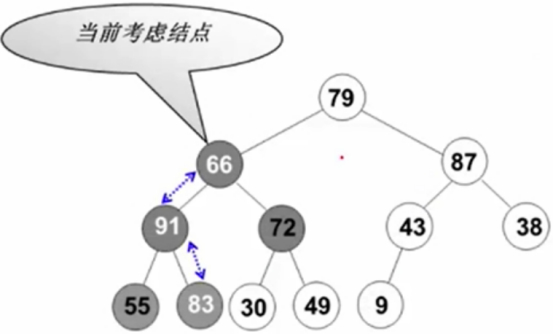
调66，91和83上去.

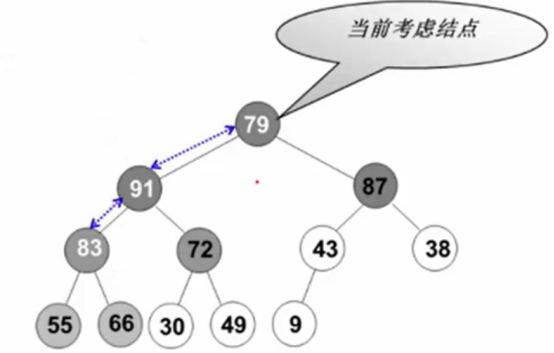
到调79的时候，左右两边已经是堆了。

在此根结点，在左右结点中找个大的。

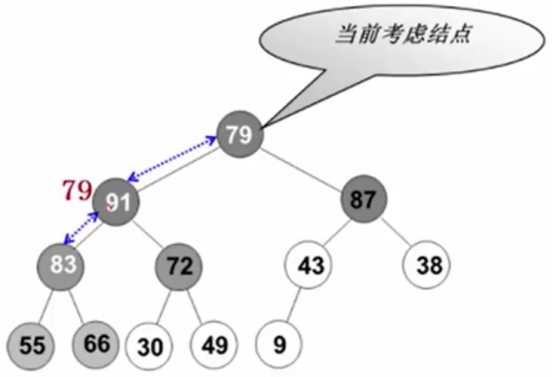
79先跟91比较，79<91。

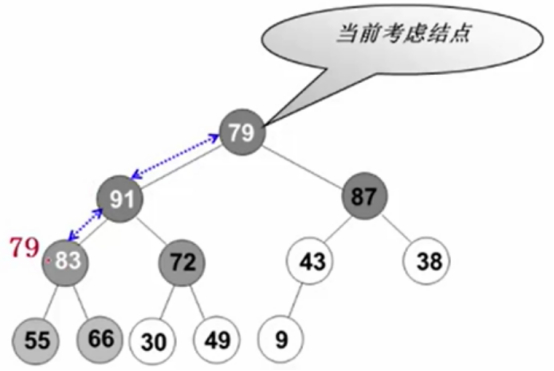
79再跟83比较，79<83。

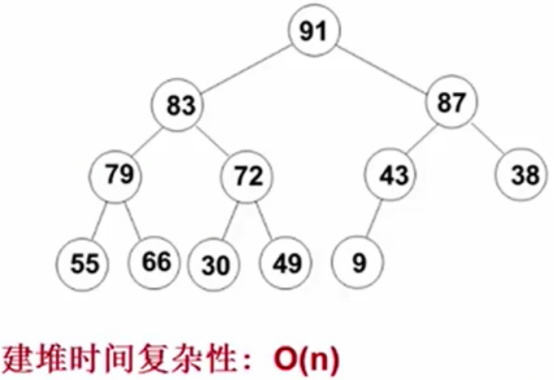
79再跟66比较，66<79。

这就形成了一个建堆的线性时间，同树的高度，时间复杂度为:O(n)，就可以完成建堆的过程。

/*
调整H->Data[]中的元素,使其满足最大堆的有序性.
这里假设所有的H->Size个元素已经存在于H->Data[]中.
*/
void BuildHeap(MaxHeap H){
	int i;
	/*
	从最后一个结点的父结点开始,到根结点1.
	*/
	for(i = H->Size/2; i > 0;i--){
		PercDown(H, i);
	}
}

/*
建造最大堆
下滤:将H中以H->Elements[p]为根的子堆调整为最大堆.
*/
void PercDown(MaxHeap H, int p){
	int Parent, Child;
	ElementType X;
	/* 取出根结点存放的值 */
	X = H->Elements[p];
	for(Parent = p; Parent * 2 <= H->Size; Parent = Child){
		Child = Parent * 2;
		if((Child != H->Size) && (H->Elements[Child] < H->Elements[Child + 1)){
			/* Child指向左右子结点的较大者 */
			Child++;
		}
		/*
		不再需要调整.
		找到了合适位置.
		*/
		if(X >= H->Elements[Child]){
			break;
		}else{
			/*
			下滤X
			*/
			H->Elements[Parent] = H->Elements[Child];
		}
	}
	H->Elements[Parent] = X;
}