5.2.1 什么是哈夫曼树

计算机中存储的实际上一个ASCII码，占一个字节，八位，最高位是0。

有等长编码和不等长编码。

此判定树，得90分以上人多，需要至少4步的判断，得60分很少，至少需要1步判断，绝大部分人都需要至少4步的判断，每个段查询频率不同，显然，此判定树不够友好。

这里把grade的值当成查找次数即可，能算出来其查找效率。

这里就不要把grade的值的当成查找次数了。

0.3至少查找2次，0.1至少查找2次。

可以有不同的方法来构造搜索树，不同搜索树的效率是不同的，需要根据不同的频率构造一个效率比较好的搜索树，这就是哈夫曼树要解决的问题。

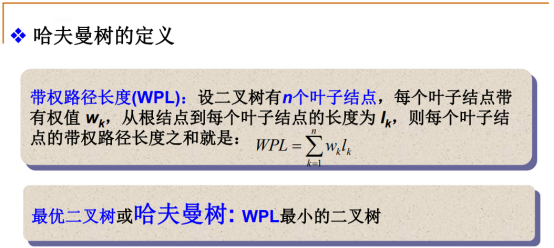
WPL=每一个叶子结点的频率或者权重*每个叶子结点到根结点路径的长度。

不同树的WPL值是不同的。

哈夫曼树的目标就是希望带权路径的长度达到最小。

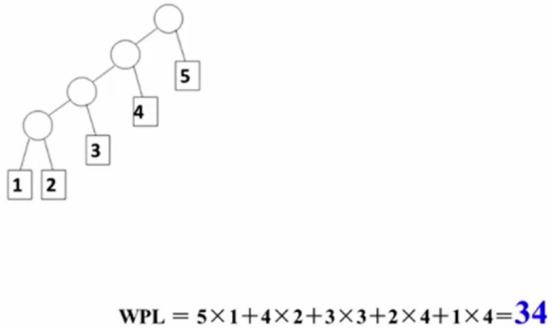
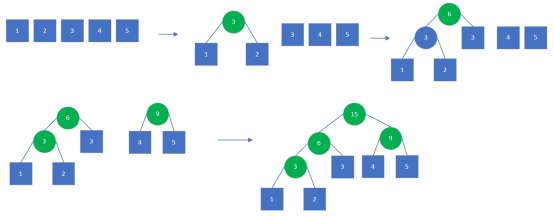
按顺序构造成树。

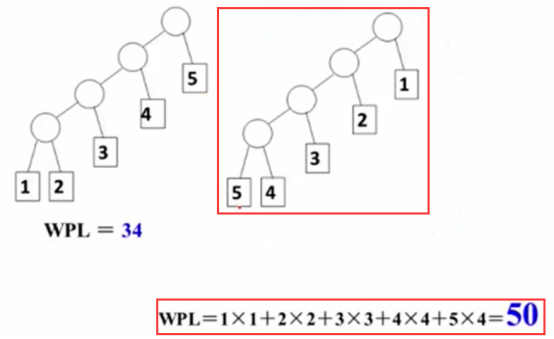
把频率低的放前面。

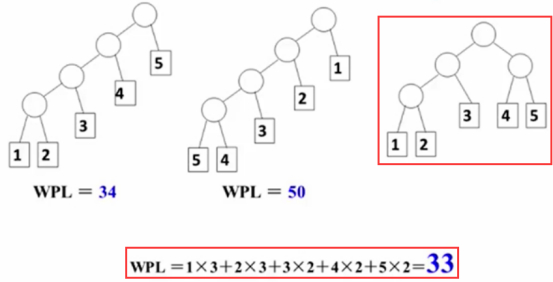
左右两边树相对均衡。

5.2.2 哈夫曼树的构造 (最小堆)

把权值从小到大进行排序，把权值最小的两个结点合并到一起，形成一个新的二叉树，这个二叉树的权值，就是合并在一起的两个权值的和。

下述第五个图形的这棵树就是哈夫曼树。

typedef struct TreeNode *HuffmanTree;
struct TreeNode{
	int Weight;
	HuffmanTree Left, Right;
}
/*
哈夫曼树的构造:把两个最小的合并,形成一个新的二叉树,
这个二叉树的权值等于原来两个权值的和,再从剩下的里面挑两个最小的,持续这个过程.
整体复杂度为O(NlogN)
主要解决问题:N个数,如何选择两个最小的值合并成新值.
这实际上是堆要解决的问题,堆效率高.
*/
HuffmanTree Huffman(MinHeap H){
	/*
	假设H->Size个权值已经存在H->Elements[]->Weight里.
	*/
	int i;
	HuffmanTree T;
	/*
	建堆.
	将H->Elements[]按权值调整为最小堆.
	*/
	BuildMinHeap(H);
	/*
	做H->Size-1次合并
	*/
	for(i = 1; i < H->Size; i++){
		/*
		建立//申请新结点
		*/	
		T = malloc(sizeof(struct TreeNode));
		/*
		从最小堆中删除一个结点,作为新T的左子节点.
		*/
		T->Left = DeleteMin(H);
		/*
		从最小堆中删除一个结点,作为新T的右子节点.
		*/
		T->Right = DeleteMin(H);
		/*
		计算新权值=等于左右权值的和
		*/
		T->Weight = T->Left->Weight + T->Right->Weight;
		/*
		将新T插入最小堆
		*/
		Insert(H, T);
	}
	T = DeleteMin(H);
	return T;
}

没有度为1的节点:因为哈夫曼树构造的时候，每次都是两个结点合并到一起形成一个新的结点，所以不可能有度为1的结点。

那么可以得出:

(

参考”3.2.1 二叉树的定义及性质”

二叉树总的结点数n=叶结点的总数n0+只有一个儿子的结点数n1+有两个儿子的结点数n2。

证明n0=n2+1。

从边的角度考虑这个问题，除了根结点没有边之外，每个结点往上看，有且仅有一条边，那么边的总数为总的结点数-1，即:总的边数=n0+n1+n2-1。

每个结点往下看，不同类型的结点，对往下边的贡献是不同的，n0结点没有儿子结点也没有边，贡献是0n0，没有边的贡献，n1结点只有一条边往下，对于边的贡献是1n1，n2结点往下/往上有两条边，对于边的贡献是2*n2。

那么n0+n1+n2-1 = 0n0 + 1n1 + 2*n2，最终约出来n0=n2+1。

)

任意两个结点左右子树交换:哈夫曼树本就是两个结点进行合并到一起的，并没强调是左右这样的顺序，放在左边或右边都可。

对同一组权值，存在不同构的两颗哈夫曼树。

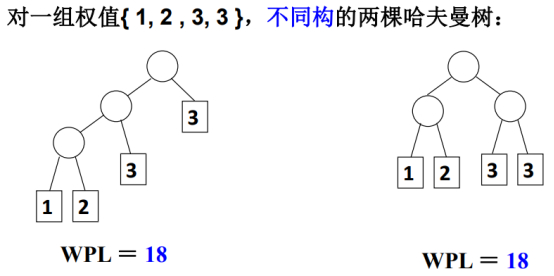
无论何种形式合并，但整个叶结点的WPL权值是一样的，也就是说最优化的值是一样的。

5.2.3 哈夫曼编码(编码空间)

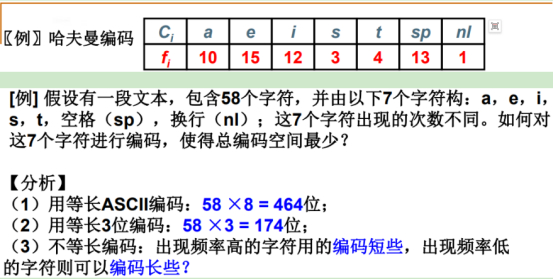
不同字符出现的频率不同，如何对字符进行编码，使其整个字符串的编码长度达到最短。

(1)

没必要用八位，总共就7个字符。

(2)

三位2的三次方是8，用3位就可以来表示八个不同的对象，这里只有7个字符，完全可以用3位编码表示7个字符中的每一个，总的编码长度174就够了。

(3)

频率高的比如可以用2位、1位。

上述对应不同字符的不同编码，这样编码显然是有问题的。

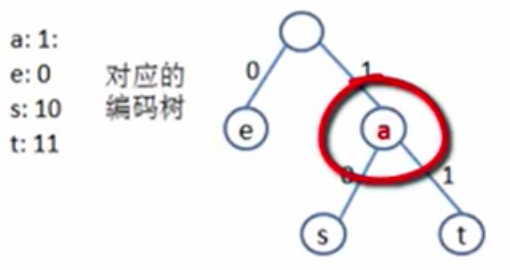
比如，s的前缀1，可以理解为a，那么a就变成s的一个前缀了。

当一个结点的编码，出现在另一个结点的编码当中，并且在树的非叶子结点上的时候，就会出现前缀。

这里存在二义性，比如都是1或10开头，到底是哪个编码呢？

要进行上述字符的编码，但每个字符出现的频率不同，可以使用等长码来进行编码。

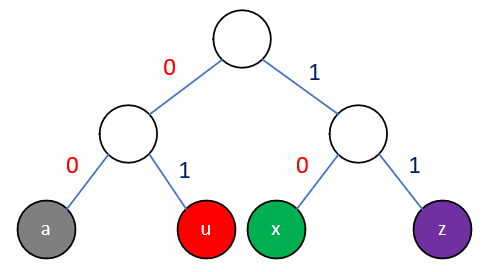
构造这样二叉树，左边0，右边1，四个对象auxz，编码都可以用两位数字表示，分别是00,01,10,11。

当所有结点都在叶子结点上的时候，就不可能出现一个字符的编码是另外一个字符的前缀。

当一个结点的编码，出现在另一个结点的编码当中，并且在树的非叶子结点上的时候，就会出现前缀。

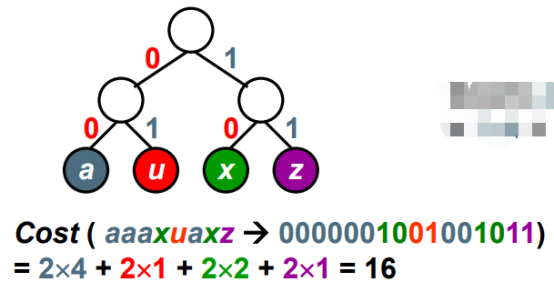
比如字符a是00代替。

构造树的目标是代价最小，频率*长度相加，此时的编码总长度为16。

所以要让编码长度最短，就是要构造一个哈夫曼树。

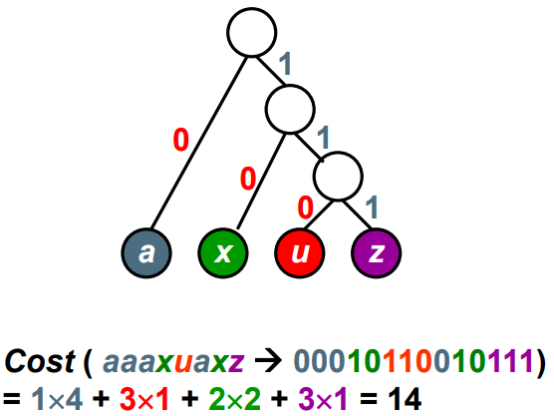
虽然这里不等长，但这里没有一个字符是另外一个字符的前缀，只要对象在叶子结点上面，就不会有二义性。

那么，如何构造一颗编码代价最小的二叉树？用哈夫曼树来构造。

要注意，带字符的放在左边，不带字符的是被合并的，放在右边。比如T4放左边，4放右边，放右边的都是被合并的新值。

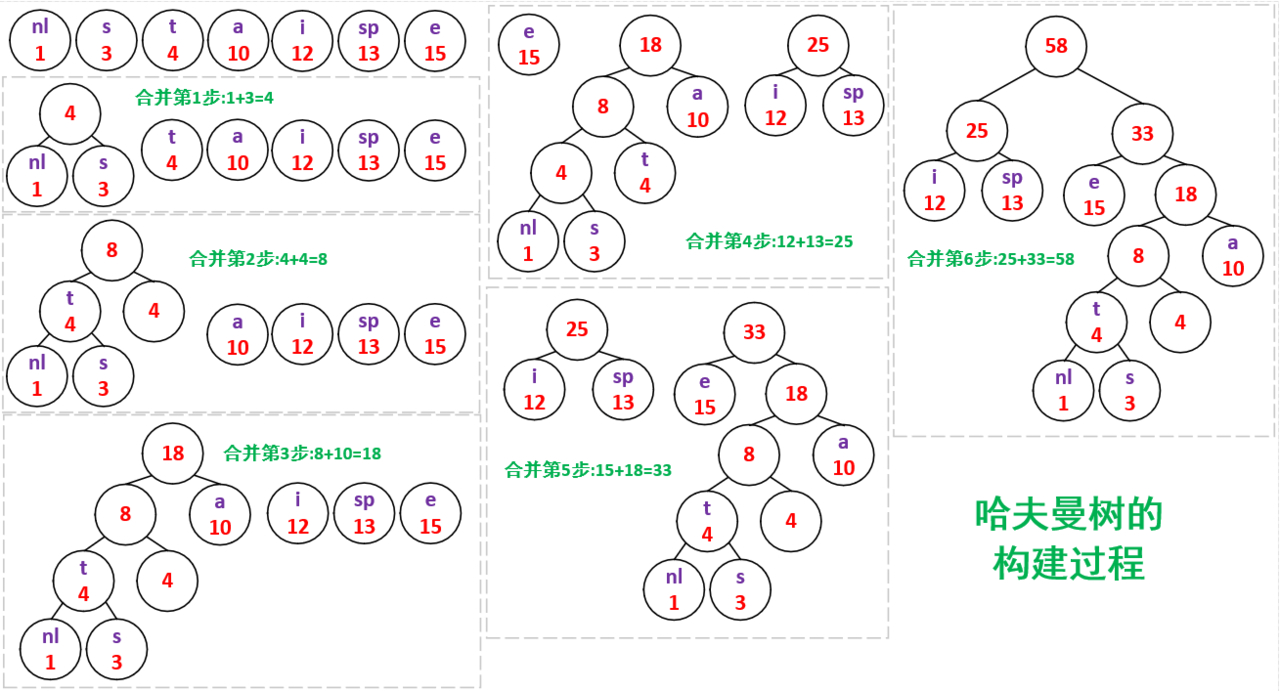
注意:当从左边往右边合并时，当合并的值大于右边剩余的值时，就停止合并，比如第三步。

于是右边的开始合并，重复上步，比如第四步。

如果没有可剩余的节点时，那么在现有的树中选出两个最小的节点进行合并，步骤同前面步骤一样，比如第五步。

当只有两个树时，直接合并，比如第六步。

哈夫曼树构建出来之后，编码也能构建出来。

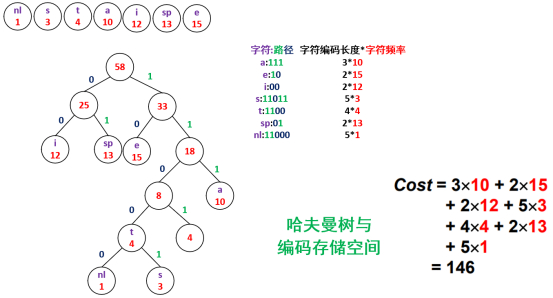
字符编码长度也可以理解成从根节点到某个子结点经过路径的边个数，也就是1和0总共出现的次数。

字符频率是某个字符在整个字符串中出现的次数。

总的代价/编码存储空间就等于所有字符的编码之和。