5.3.1 集合的表示

主要运算:两个集合合并与查某个元素属于某个集合。

如果A和B连接在一起，B和C连接在一起，那么A和C就连在一起，这种连接要传递性。

两个电脑连在一起，就把这俩集合合并。

是否联通，要确认两个电脑是否属于统一集合，相同集合就相连，否则不相连。

这俩问题相当于如何管理一堆集合？

一个把两个集合合并在一起，一个查某个元素属于哪个集合，这种问题叫做并查集。

要么要思考，如何存储一个集合？

俩集合合并到一起，相当于两棵树合并到一起，形成一颗更大的树。

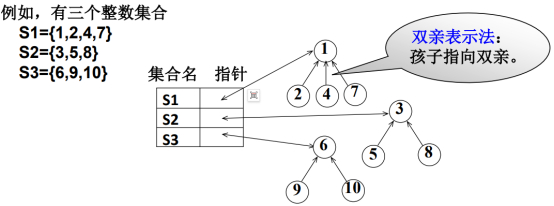
查某个元素属于某个集合，是直接去找树根。

两棵树合并，只要把一个根接到另外一根即可。

在并查操作过程中，不存在已知一个结点找儿子是谁，而是找父亲是谁，这样就能很快的找到根，这是树的一种表示方法，这叫双亲表示法，这里，每个结点的指针都指向父亲。

而二叉树，一个结点指向儿子，一个结点指向父亲。

这种双亲表示法的树结构如何存储？

/*
集合(课程提供讲解版)
*/
/*
集合的数组表示
*/
typedef struct{
	/*
	元素内容
	*/
	ElementType Data;
	/*
	负数表示根结点,非负数表示双亲节点的下标.
	*/
	int Parent;
} SetType;

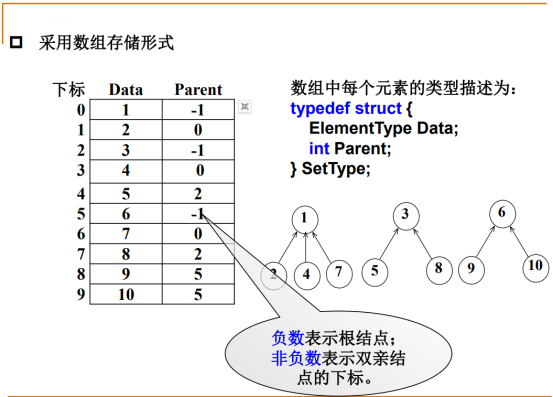
数组中的每一行是分量。

分量下标:每个元素的下标值，标记每个元素所在数组中的位置。

分量data:每个元素的基本信息，比如1-10。

分量Parent:指向每个元素父结点所在数组下标的位置，没有父亲用-1表示。

5.3.2 集合的操作(file transfer优化与对比)

查询元素所在集合(根结点表示)

/*
查找某个元素所在的集合(用根结点表示一个集合)
在数组S中查找值为X的元素所属的集合
*/
int Find(SetType S[], ElementType X){
	int i;
	/*
	从数组的头上一个个往后找
	当Data == X时退出集合
	*/
	for(i = 0; i < MaxSize && S[i].Data != X; i++);
	/*
	未找到X,返回-1.
	如果x < MaxSize,证明X在0-MaxSize之间.
	*/
	if( x >= MaxSize){
		return -1;
	}
	/*
	找到X所属集合,返回树根结点在数组S中的下标.
	当i = S[i].Parent,那么Parent>0就一直往上走.
	当Parent=-1,就是根结点.
	*/
	for( ; S[i].Parent >= 0; i = S[i].Parent);
	/*
	退出时,i=树的根的下标.
	*/
	return i;
}

集合的并运算(小合并大)

/*
集合的并运算
分别找到X1和X2两个元素所在集合树的根节点.
如果它们不同根,则将其中一个根结点的父结点指针设置成另一个根结点的数组下标.
*/
void Union(SetType S[], ElementType X1, ElementType X2){
	int Root1, Root2;
	Root1 = Find(S, X1);
	Root2 = Find(S, X2);
	/*
	当X1和X2不属于同一个子集时,才需要合并.
	*/
	if( Root1 != Root2){
		S[Root2].Parent = Root1;
	}
}

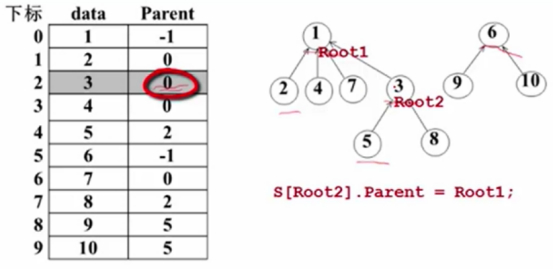
把元素2和元素5合并在一起，那么通过2找到1，通过5找到3，那么把Root2挂到Root1中。

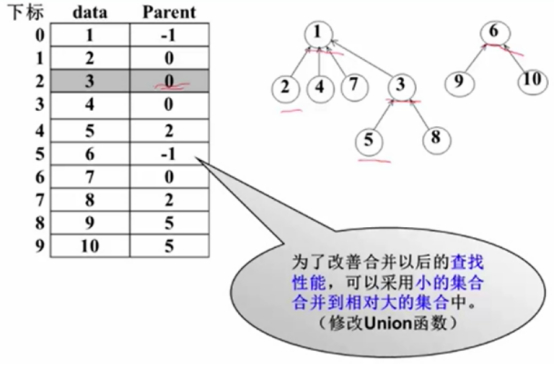
这样不断Union时，树会越来越大，越来越高，导致Find从根节点开始往上一层层找时，效率越来越差。

这样，为了保证集合后续的查询效率，可以采用小的集合合并到相对大的集合中去。

当树越来越庞大时，需要知道每个集合有多少元素，只需要根节点记录，其他结点不需要记录，如果在数组中增加一个分量，那么增加的空间是不需要的。

那么可以使用Parent，负数代表根结点，而这个树的绝对值代表集合的元素个数，就可以推出每个集合的大小了，那么就需要修改Union函数，来判别集合大小并设置大集合与小集合的挂载方式。

源码

/*
集合的定义与并查操作(课程提供最终版)
*/
#define MAXN 1000/* 集合最大元素个数 */
typedef int ElementType;/* 默认元素可以用非负整数表示 */
typedef int SetName;/* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN];/* 假设集合元素下标从0开始 */

/*
查找某个元素所在的集合
*/
SetName Find(SetType S,ElementType X){
	/* 默认集合元素全部初始化为-1 */
	if(S[X] < 0){
		/* 找到集合的根 */
		return X;
	}
	else{
		/* 路径压缩 */
		return S[X] = Find(S, S[X]);
	}
}

/*
集合的并运算
这里默认Root1和Root2是不同集合的根结点.
保证小集合并入大集合.
*/
void Union(SetType S, SetName Root1, SetName Root2){
	if(S[Root2] < S[Root1]){
		/* 如果集合2比较大 */
		/* 集合1并入集合2  */
		S[Root2] += S[Root1];
		S[Root1] = Root2;
	}
	else if(S[Root2] > S[Root1]){
		/* 如果集合1比较大 */
		/* 集合2并入集合1  */
		S[Root1] += S[Root2];
		S[Root2] = Root1;
	}
}