6.1.1图的定义

图:强大的数据结构。

建立多对多的关系。

六度空间理论:人与人之间的关系，可以用边来表示。

全球13亿互联网用户之间的联系。

地铁两个站之间路径最短，最便宜的路线。

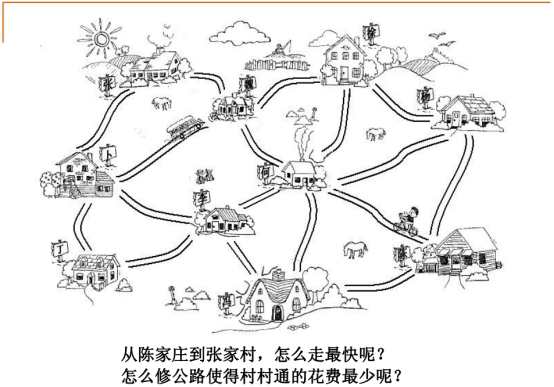
图中非常经典的最小生成树问题。

图的强大，是因为包括了线性表(一对一)和树(一对多)。

可以认为，线性表和图都是图的一个特殊情况。

边是顶点对:如果这条边是无向边，无所谓方向，可以从V到W，也一定可以从W到V，双向道路，可以用圆括号表示。

有向边:单行线，只能从V到W，不可以W到V，尖括号表示。

重边:两个顶点之间是无向边的话，默认只有一条，不可能有很多条。

自回路:当说道有向边时，一定从一个顶点到另一个顶点，不可能指回自己。

在介绍一个结构时，肯定先是从抽象数据类型定义开始的。

三要素:类型名称、数据对象集(什么东西构成)、操作集。

注意:图可以没有边，但至少有一个顶点。

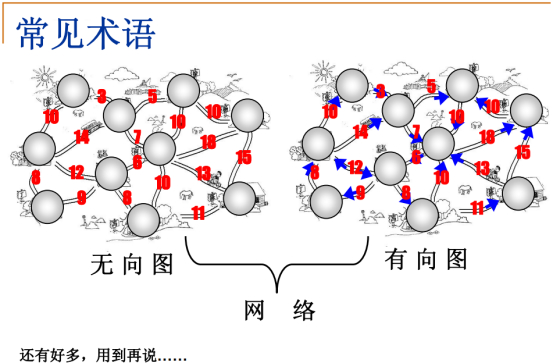
无向图:图中里面所有边都是无所谓方向的。

有向图:图中里面的边可能单向，也可能双向，即:方向对图很重要。

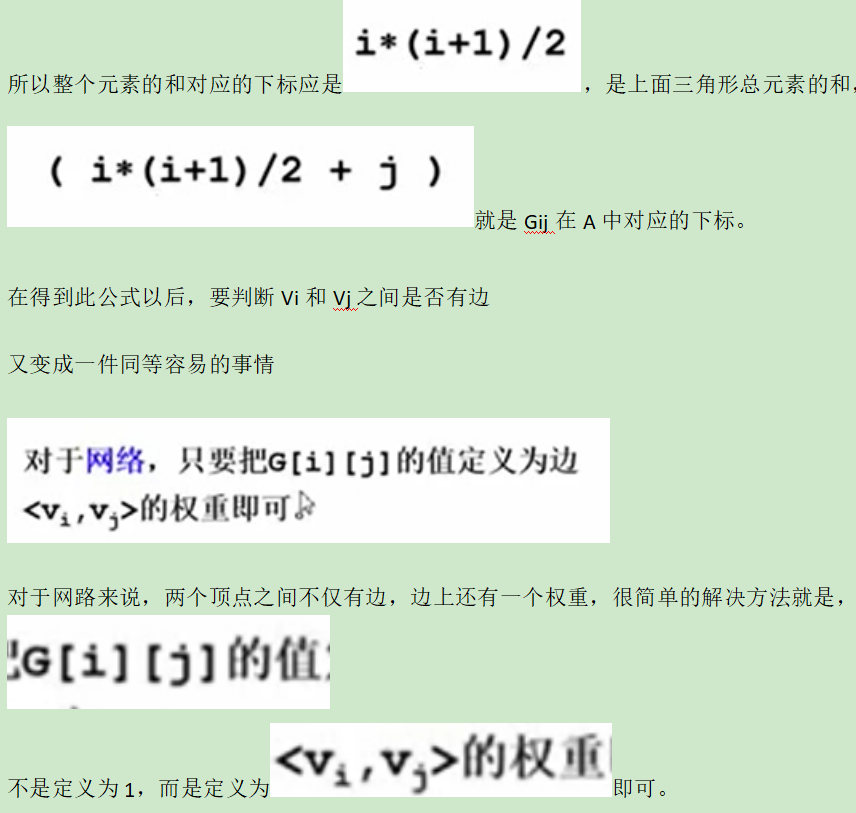
每条边的数字:权重，可定义为这条路线的长度，带权重图的另外名称叫网络。

6.1.2邻接矩阵表示法

用二维数组去表示一个图，有N个顶点的话，假设这个顶点是从0到N-1来编号的，表示它们有一个非常简单的做法。

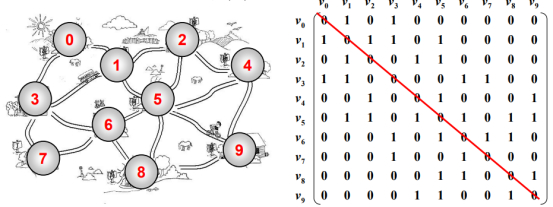
如果二维数组，某个坐标，那么右边用1表示，没边用0表示。

特点:

(1)因为不允许自回路的边，所以我们认为一个结点到他自己是不需要边的，所以这个对角阵不全都是0。

(2)矩阵是对称的。以这条对角线为基础，如果这个元素是1，那么跟他对称的这个元素的值一定是1，0同理。

比如G03，

如果是1的话，那么0和3之间是有一条边的。

当然，相对的3和0之间也有一条边的。
所以，G30这条边也是得是存在的。

这里把一条边存了两次，有必要吗？

邻接矩阵-无向图存储节省空间与元素位置

对于无向图，邻接矩阵中有一半空间是被浪费的。

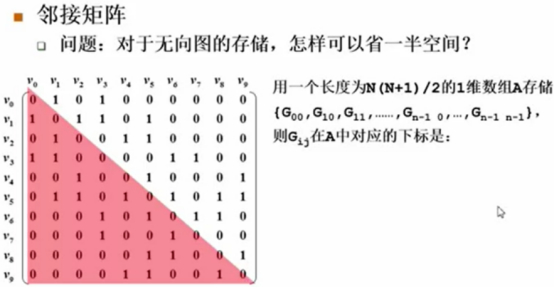
真的只存储一半的元素，比如只存下三角，技巧用一维数组，存下三角矩阵的额元素，存法按行来，

A0=G00

从上到下，从左到右一行行的来存储，当然空间省了，带来的麻烦就是，元素不好找了，要判断ij两个元素之间是否右边的时候，如果用原来二维数组的存法，只要去看Gij是否等于1就可以了，现在Gij被藏在A里面，哪个位置？

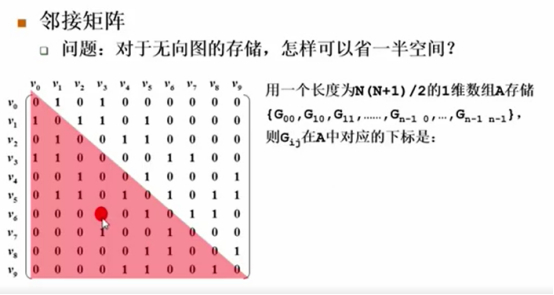
比如一个元素处在Gij的位置，在A中到底是第几个元素呢？

数一下在它前面的个数，前面i-1行元素的总个数，再加上

这是列号。这边是应该有J个元素。

邻接矩阵-好处

现在知道图可以使用邻接矩阵来表示。

邻接矩阵-邻接点

邻接点:有直接的边跟它相连的所有的顶点，叫这个点的邻接点。

如何用邻接矩阵去找所有的邻接点呢？

简单。

对无向图，只要沿着这个矩阵的一行扫描过去，所有不是0的那些顶点就一定有边跟它直接相连的。

有向图，这个邻接矩阵不一定是对称的，所以不仅要扫描一行，还要扫描一列，才能找到根它有直接边相连的邻接点。

邻接矩阵-度

度:跟这个顶点相关的所有边的个数，对于有向图来说，俩概念，出度、入度。

如何计算任意一个顶点的度？

无向图:扫描一行或者这一列，非0元素的个数，把所有的1加起来就是度。

出度:扫描第i行1的个数，从Vi这个顶点发出去的所有的边。

当扫描第i列的时候，得到的就是所有指向Vi这个顶点的边的个数。

邻接矩阵-稀疏图与稠密图/完全图

在图里有很多很多的结点，一共只有两条边，有邻接矩阵存储时，此邻接矩阵长啥样呢？

有一大堆的0，非常浪费空间。

稀疏图:点很多，相对来说边很少，矩阵中会有大量的0元素，也就是无效的元素。

如果图不是很稀疏，稠密图。

完全图/稠密图:给N个结点，任意两个结点直接都有一条边，边数是达到极大的图。

相当于矩阵中所有的元素都是1，这么存就没有一个元素是浪费的，很核算。

稀疏图:浪费的不仅仅是空间的问题，还浪费时间。

用邻接矩阵，不得不把邻接矩阵中的所有元素都扫描一遍，数有多少个1，问题是1很少，这样浪费的不仅是空间，而且是时间。

6.1.3邻接表表示法

邻接矩阵在表示稀疏图时，不方便，比较浪费空间和浪费时间，为解决此问题的方法是邻接表。

这样如果有大量0的话，那么这些0都不会出现在链表中，通过此方法来省空间。

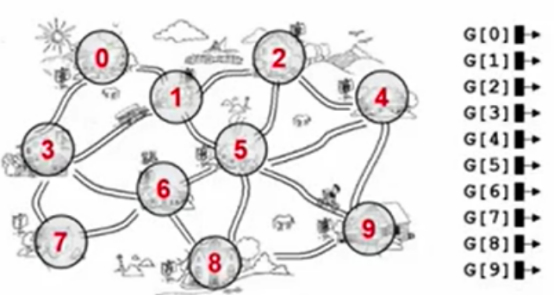
这个小镇，如何用邻接表存储呢？

首先，为每一个结点开一个指针数组，一共10个结点，一个长度为10的数组，数组的元素是一个头指针。

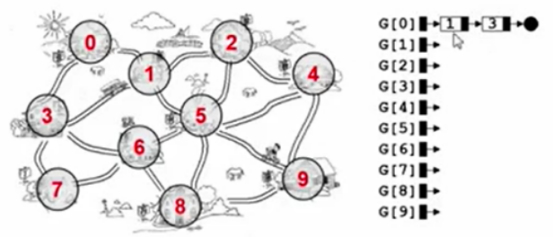
0跟1和3相连。

所以串起来此链表。

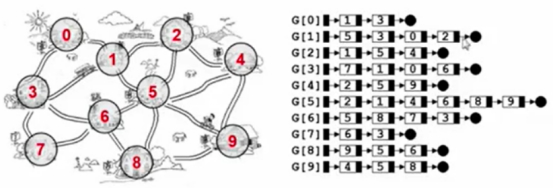
0和3、2和5等都是相连的，以此类推，在这个链表上就会形成这样的邻接表来表示此图。

要注意的是，邻接表的表示法不是唯一的，因为在这个串上面，这些结点的顺序并不重要，需要仔细数一下这个图占了多少空间。

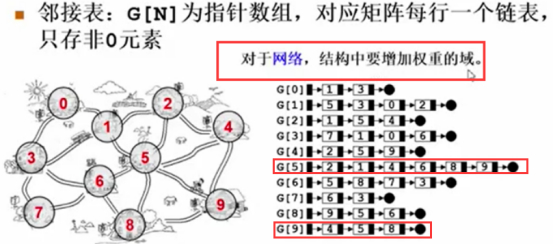
真的很节省空间吗？

在邻接矩阵的表示法中，每一条边占了一个整数的位置，那么每一条边是如何存储的呢？

5链表中有9，9链表中有5，所以一条边必定存了两遍。

存了顶点的整数编号，指针指向下一个，所以一条边占差不多两个整数。

而且对于网络来说，结构中还要增加权重的域，比如可以把1变成权重。

所以，如果要用邻接表的话，那么一定要够稀疏才划算。

第1个:

找Vi的所有邻接点，顺着Gi的链表一直走下去，就把它所有的邻接点都访问到了，没有任何不必要的零点。

第2个:

整个邻接表用了多少空间呢？

每个结点，如果不考虑权重的话，那么至少是需要两个域的。

(接”问题”)

第3个:

是否方便计算任意一个结点的度?取决于在说一个什么图?

无向图:只要访问顶点所代表的链表，数一下这个链表一共串了多少条边，就知道度是多少。

有向图:

出度计算:只能计算出度因为串在Vi对应的链表上面，只是从Vi往外指出去的那些边。

入度计算:正邻接表存的是邻接矩阵的每一行存成了一个链表，逆邻接表是把邻接矩阵的每一列再形成一个链表，那相应的这一列存的就是指向它自己的边，这边可以比较方便的计算入度。

第4个:

非常麻烦的问题。

图的表示不是说只能用邻接矩阵或者邻接表，用的方法取决于要解决的具体问题。

C语言代码 : 图的建立-邻接矩阵表示

#include<stdio.h>
/*
图的建立:邻接矩阵的表示
*/
int main(void){
	return 0;
}
/* 最大顶点数设为100 */
#define MaxVertexNum 100
/* ∞设为双字节无符号整数的最大值65535*/
#define INFINITY 65535
/* 用顶点下标表示顶点,为整型 */
typedef int Vertex;
/* 边的权值设为整型 */
typedef int WeightType;
/* 顶点存储的数据类型设为字符型 */
typedef char DataType;

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
	/* 有向边<V1, V2> */
	Vertex V1, V2;
	/* 权重 */
	WeightType Weight;
};
typedef PtrToENode Edge;
/* 图结点的定义 */
typedef struct GNode *PtrToENode;
struct GNode{
	int Nv;/* 顶点数 */
	int Ne;/* 边数   */
	WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
	/* 注意：很多情况下，顶点无数据，此时Data[]可以不用出现 */
	DataType Data[MaxVertexNum];      /* 存顶点的数据 */
}
/* 以邻接矩阵存储的图类型 */
typedef PtrToENode MGraph;
/* 
初始化一个有VertexNum个顶点但没有边的图 
*/
MGraph CreateGraph(int VertexNum){
	Vertex V, W;
	MGraph Graph;
	/* 建立图 */
	Graph = (MGraph)malloc(sizeof(struct GNode));
	/* 顶点数 */
	Graph->Nv = VertexNum;
	/* 边数   */
	Graph->Ne = 0;
	/* 初始化邻接矩阵 */
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
    for(V = 0; V < Graph->Nv; V++){
    	for(W = 0; W < Graph->Nv; W++){
    		Graph->G[V][W] = INFINITY;
		}
	}
    return Graph;
}

/* 插入边 <V1, V2> */
void Insert(MGraph Graph, Edge E){
	Graph->G[E->V1][E->V2] = E->Weight;
	/* 若是无向图，还要插入边<V2, V1> */
	Graph->G[E->V2][E->V1] = E->Weight;
}


MGraph BuildGraph(){
	MGraph Graph;
	Edge E;
	Vertex V;
	int Nv, i;
	/* 读入顶点个数 */
	scanf("%d", &Nv);
	/* 初始化有Nv个顶点但没有边的图 */
	Graph = CreateGraph(Nv);
	/* 读入边数 */
	scanf("%d",&(Graph->Ne));
	/* 如果有边 */
	if(Graph->Ne != 0){
		/* 建立边结点 */
		E = (Edge)malloc(sizeof(struct ENode));
		/* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
		for(i = 0; i < Graph->Ne; i++){
			scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
			/* 注意：如果权重不是整型，Weight的读入格式要改 */
			InsertEdge(Graph, E);
		}
	}
	/* 如果顶点有数据的话，读入数据 */
	for(V = 0;V < Graph->Nv;V++){
		scanf("%c", &(Graph->Data[V]));
	}
	return Graph;
}

C语言代码 : 图的建立-邻接表表示

#include<stdio.h>
/*
图的建立:邻接表的表示
*/
int main(void){
	return 0;
}
/* 最大顶点数设为100 */
#define MaxVertexNum 100
/* 用顶点下标表示顶点,为整型 */
typedef int Vertex;
/* 边的权值设为整型 */
typedef int WeightType;
/* 顶点存储的数据类型设为字符型 */
typedef char DataType;
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
	/* 有向边<V1, V2> */
	Vertex V1, V2;
	/* 权重 */
	WeightType Weight;
}
typedef PtrToENode Edge;
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
	/* 邻接点下标 */
	Vertex AdjV;
	/* 边权重 */
	WeightType Weight;
	/* 指向下一个邻接点的指针 */
	PtrToAdjVNode Next;
}
/* 顶点表头结点的定义 */
typedef struct Vnode{
	/* 边表头指针 */
	PtrToAdjVNode FirstEdge;
	/* 存顶点的数据 */
	DataType Data;
	/* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
	/* 顶点数 */
	int Nv;
	/* 边数   */
	int Ne;
	/* 邻接表 */
	AdjList G;
}
/* 以邻接表方式存储的图类型 */
typedef PtrToGNode LGraph;
/* 初始化一个有VertexNum个顶点但没有边的图 */
LGraph CreateGraph(int VertexNum){
	Vertex V;
	LGraph Graph;
	/* 建立图 */
	Graph = (LGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
    /* 初始化邻接表头指针 */
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
    for(V = 0; V < Graph->Nv; V++){
    	Graph->G[V].FirstEdge = NULL;
	}
	return Graph;
}

void InsertEdge(LGraph Graph, Edge E){
	PtrToAdjVNode NewNode;
    /* 插入边 <V1, V2> */
    /* 为V2建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    /* 将V2插入V1的表头 */
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V2].FirstEdge = NewNode;
}

LGraph BuildGraph(){
	LGraph Graph;
	Edge E;
	Vertex V;
	int Nv, i;
	/* 读入顶点个数 */
	scanf("%d", &Nv);
	/* 初始化有Nv个顶点但没有边的图 */
	Graph = CreateGraph(Nv);
	/* 读入边数 */
	scanf("%d", &(Graph->Ne));
	/* 如果有边 */
	if(Graph->Ne != 0){
		/* 建立边结点 */
		E = (Edge)malloc(sizeof(struct ENode));
		/* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
		for(i = 0; i < Graph->Ne; i++){
			scanf("%d %d %d",&E->V1, &E->V2, &E->Weight);
			/* 注意：如果权重不是整型，Weight的读入格式要改 */
			InsertEdge(Graph, E);
		}
	}
	/* 如果顶点有数据的话，读入数据 */
	for(V = 0; V < Graph->Nv; V++){
		scanf("%c", &(Graph->G[V].Data));
	}
	return Graph;
}