如何把一个抽象的图变成C语言代码。

算法前提:有一个图。

图的表示:邻接矩阵、邻接表。

邻接矩阵表示的图结点的结构

在程序中对应一个二维数组。

无权图:

如果Vi和Vj有一条边的话，那么第[i][j]这个元素等于1，否则0。

有权图:

当有一条边的话，对应权重，否则有可能是0和无穷大。

#include<stdio.h>
/*
用邻接矩阵表示图
*/
int main(void){
	return 0;
}
/*
指向此结点的指针
*/
typedef struct GNode *PtrToGNode;
/*
图的结点结构体
*/
struct GNode{
	/*
	重要变量:顶点数
	*/
	int Nv;
	/*
	重要变量:边数
	*/
	int Ne;
	/*
	二维数组的大小由所有顶点的数量决定.
	这里二维数组的类型WeightType是抽象写法,大多情况是整型,也可是double、字符类型.
	*/
	WeightType G[MaxVertexNum][MaxVertexNum];
	/*
	如果是考试,那么上述就够用了.
	当处理某一类问题时,可能图里的每个顶点<Vi,Vj>都各自的意义,存一些东西,也可能是一个struct.
	*/
	DataType Data[MaxVertexNum];
};
/*
以邻接矩阵存储的图类型
M:matrix矩阵缩写
*/
typedef PtrToGNode MGraph;

邻接矩阵表示的图-初始化

/*
MGraph初始化:初始化一个有VertexNum个顶点但没有边的图.
图中可以没有边,但至少要有一个顶点.
*/
/*用顶点下标表示顶点,为整型.*/
typedef int Vertex;
MGraph CreateGraph(int VertexNum){
	/*
	第1部分
	声明图结点:结点一旦声明,矩阵空间就有了.
	顶点类型Vertext这里为整型,因为是用顶点的下标来表示一个顶点的.
	*/
	Vertext V, W;
	MGraph Graph;
	Graph = (MGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
	/*
	第2部分
	*/
	/*
	注意:这里默认顶点编号从0开始,到(Graph->Nv - 1).
	尽管表面上看起来是整型,本质上和Vertext是完全不同的东西.
	这里没有用平时用到的i和j作为循环变量,不要混淆.
	*/
	for(V = 0; V < Graph->Nv; V++){
		for(W = 0; W < Graph->Nv; W++){
			/*0或INFINITY无穷大*/
			/*
			初始化无权图:此图中邻接矩阵任意一对顶点V和W的边定义都为0,表示它们之间没有边.
			初始化有权图:初始化为INFINITY,定义成很大的数,表示顶点之间没有边.
			*/
			/*
			邻接表LGraph中没有边:每一个顶点跟链表都是空的.
			对于Graph里面的邻接表,每个顶点V来说,FirstEdge指向第一条边的这个指针都是空的.
			邻接矩阵MGraph中没有边:任意一对顶点之间,二维数组的值是1或无穷大.
			*/
			Graph->G[V][W] = 0;
		}
	}
	return Graph;
}

邻接矩阵表示的图-插入边

/*
向MGraph中插入边
*/
/*
定义指向边结点的指针
*/
typedef struct ENode *PtrToENode;
/*
定义边结点
*/
struct ENode{
	/*
	一条边是由两个顶点来决定的
	*/
	/*
	无权图:仅定义Vertex即可.
	有向边:从V1指向V2的有向边时定义这个.V1出发点,V2终点.
	*/
	Vertex V1, V2;
	/*
	有权图:定义权重.
	*/
	WeightType Weight;
}
typedef PtrToENode Edge;

void InsertEdge(MGraph Graph, Edge E){
	/*
	有向图:插入边<V1, V2>
	对于邻接矩阵,插入一条边就是把相应的权重赋给相应的邻接矩阵这个元素就可以了.
	*/
	Graph->G[E->V1][E->V2] = E->Weight;
	/*
	无向图:还要插入边<V2, V1>
	赋值为这条边的权重.
	*/
	Graph->G[E->V2][E->V1] = E->Weight;
}

邻接矩阵表示的图-建立图

完整建立

/*
完整的建立图MGraph
Nv所有顶点个数 Ne总边数
每行的边信息:V1边的初始点 V2边的终点 Weight权重
*/
MGraph BuildGraph(){

	MGraph Graph;
	Edge E;
	Vertex V;
	int Nv, i;

	scanf("%d", &Nv);

	Graph = CreateGraph(Nv);

	scanf("%d", &(Graph->Ne));

	/*
	读进来边数=0,那么图本身没有边.
	*/
	if(Graph->Ne != 0){
		/*
		临时边结点
		*/
		E = (Edge)malloc(sizeof(struct ENode));
		for(i = 0; i < Graph->Ne; i++){
			scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
			/*
			读入边并插入图中.
			*/
			InsertEdge(Graph, E);
		}
	}
	/*
	如果顶点有数据的话,那么读入数据.
	*/
	for(V = 0; V < Graph->Nv; V++){
		scanf("%c", &(Graph->Data[V]));
	}

	return Graph;
}

临时建立

/*
临时的建立图MGraph(考试)
Nv所有顶点个数 Ne总边数
如果这个邻接矩阵就是整型的,那么就不需要再返回这个图了.
*/
int G[MAXN][MAXN], Nv, Ne;
void BuildGraphTemp(){
	int i, j, v1, v2, w;
	scanf("%d", &Nv);
	/*
	CreateGraph
	*/
	for(i = 0; i < Nv; i++){
		for(j = 0; j < Nv; j++){
			G[i][j] = 0;/*0或INFINITY无穷大*/
		}
	}
	scanf("%d", &Ne);
	for(i = 0; i < Ne; i++){
		scanf("%d %d %d", &v1, &v2, &w);
		/*
		InsertEdge
		*/
		G[v1][v2] = w;
		G[v2][v1] = w;
	}
}

邻接表表示的图结点的结构

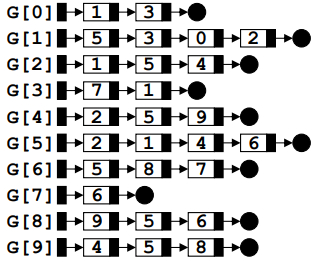
有向图:

比如G[2]，这个链表表示，有一条边，从2到1，从2到5，从2到4。

无向图:

一条边会被存两次，比如从1到5有一条边的话，那么从5到1也应该有一条边。

#include<stdio.h>
/*
用邻接表表示图
数组中每一个指针对应着矩阵每行的一个链表.
*/
int main(void){
	return 0;
}
/*
指向结点的指针
*/
typedef struct GNode *PtrToGNode;
struct GNode{
	/*顶点数*/
	int Nv;
	/*边数*/
	int Ne;
	/*核心邻接表*/
	AdjList G;
}
/*
以邻接表方式存储的图类型
*/
typedef PtrToGNode LGraph;

typedef struct AdjVNode *PtrToAdjVNode;
/*
链表里代表每一条边的结点.
虽然代表一条边,但是不需要存两个顶点,因为它已经放在某个顶点的链表中了,这条边的出发点已经决定了它在谁家的链表中了.
所以在这条边的结点中,只需要存这个顶点的邻接点/终点(的下标)即可,比如G[9],边4的邻接点是5.
*/
struct AdjVNode{
	/*
	邻接点下标
	*/
	Vertex AdjV;
	/*
	有权图需要存:边的权重
	*/
	WeightType Weight;
	/*
	链表中的结点指向下一个结点的指针
	*/
	PtrToAdjVNode Next;
}
/*
结点
*/
typedef struct Vnode{
	/*
	指针指向一个边的结点:边结点的类型AdjVNode
	指针命名FirstEdge,也就是第一条边,比如图例G[9]指向的第一条边4.
	*/
	PtrToAdjVNode FirstEdge;
	/*
	存顶点(自定义)数据.
	DataType可能是整型、double、struct等类型.
	*/
	DataType Data;
} 
/*
AdjList邻接表自定义类型数组.
数组大小等于顶点数量.
每个元素都是一个结点.
*/
AdjList[MaxVertexNum];

邻接表表示的图- 初始化

/*
LGraph初始化
初始化一个有VertexNum个顶点但没有边的图.
*/
/*用顶点下标表示顶点,为整型.*/
typedef int Vertex;
LGraph CreateGraph(int VertexNum){
	Vertex V, W;
	LGraph Graph;
	Graph = (LGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
	/*
	上述模块:MGraph跟LGraph的结构实现一样
	*/
	/*
	注意:这里默认顶点编号从0开始,到(Graph->Nv - 1)结束.
	*/
	for(V = 0; V < Graph->Nv; V++){
		/*
		邻接表LGraph中没有边:每一个顶点跟链表都是空的.
		对于Graph里面的邻接表,每个顶点V来说,FirstEdge指向第一条边的这个指针都是空的.
		这里初始化了LGraph中所有空的边.
		邻接矩阵MGraph中没有边:任意一对顶点之间,二维数组的值是1或无穷大.
		*/
		Graph->G[V].FirstEdge = NULL;
	}
	return Graph;
}

邻接表表示的图- 插入边

/*
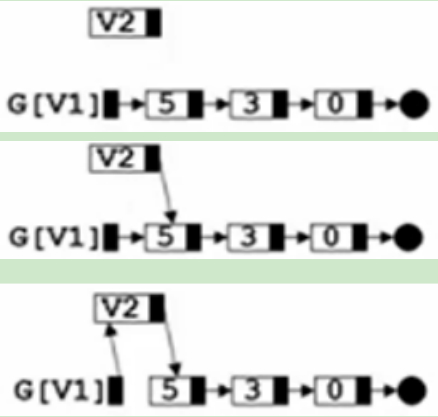
向LGraph中插入边
插入边的过程就是把一个顶点插入到一个链表里面去的过程
*/
void InsertEdge(LGraph Graph, Edge E){
	PtrToAdjVNode NewNode;

	/*
	有向图:插入边<V1,V2>
	要对V2建立一个边的结点,然后把这个结点插到V1所在的这个链表里面.
	可以插入到链表的任意位置,但从实现角度来讲,插入链表的头部最简单.
	*/
	/*
	为V2建立新的邻接点
	*/
	NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
	NewNode->AdjV = E->V2;
	NewNode->Weight = E->Weight;
	/*
	将V2插入V1的表头
	V2的next指针要指向G[V1]第一条边FirstEdge指向这个结点)
	*/
	NewNode->Next = Graph->G[E->V1].FirstEdge;
	/*
	把G[V1]的FirstEdge换个方向指向V2.
	此时:
	新结点的next指向G[V1]的第一条边.
	G[V1]的第一条边指向新的结点.
	完成插入.
	*/
	Graph->G[E->V1].FirstEdge = NewNode;


	/*
	无向图:还要插入边<V2,V1>
	*/
	/*
	为V1建立新的邻接点
	*/
	NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
	NewNode->AdjV = E->V1;
	NewNode->Weight = E->Weight;
	/*
	将V1插入V2的表头
	*/
	NewNode->Next = Graph->G[E->V2].FirstEdge;
	Graph->G[E->V2].FirstEdge = NewNode;

}