YAZONG 我的开源

(数据结构)第七讲-图(7.1 最短路径问题)

  , ,
0 评论 • 0 浏览

7.1.1 概述

生活中的案例-地铁:

对应图的顶点:

一个个的站点，

路径:两个站点之间有直通路线，那么两个站点之间就有一条边。

最短路程:最短距离。

权重:两个站点之间的距离。

比如:

要找的是从A站到B站的所有可达路径中间，距离最短的路程是哪条？

另一种问法，最便宜的路程是哪条？

另一种问法，经停站最少的路程是哪条，最快？跟边的个数相关。

这几种问法，区别在于上述的权重，赋予其何种含义？

这些问题如何抽象？

可以统一抽象归纳成一个图论的最短距离问题。

image.png

网络:带权的图里面。不同的问题，针对不同的边的权重的值的定义。

最短路径问题说的不是一个问题，而是一套问题。

image.png

除下述在特殊情况的更聪明的解决方法外，普通的解决方案是:解决单源最短路径问题，可以把算法在每个顶点都执行一遍，这样就自然得到多源最短路问题的解。

单源最短路径， 可以是有向图，也可以是无向图，二者算法一样 。

7.1.2 无权图的单源最短路径算法(BFS)(邻接表存储)

简介(有向无权图)

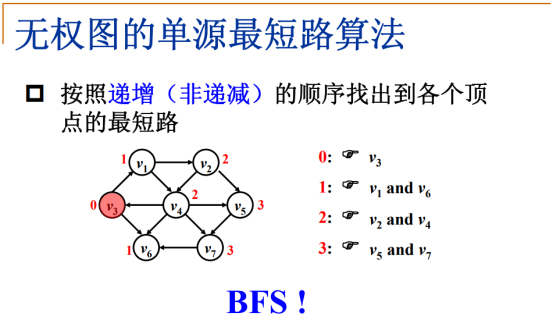
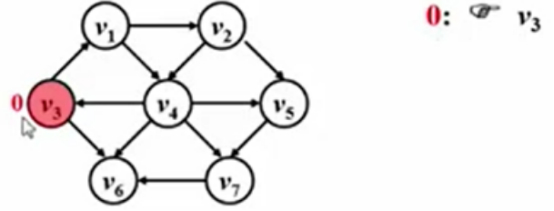
image.png

image.png

从V3出发，去找它到其他各个顶点的最短路程。

路径长度为0的顶点:

此时，从一个路径长度为0的路径出发，源点到它自己是不用走路的，所以其路径长度为0。

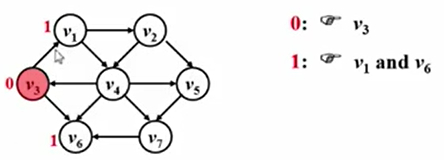
image.png

路径长度为1的顶点:

V1和V6到源点V3的距离是1，二者是V3直接的邻接点。

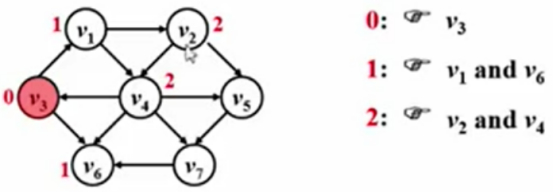
image.png

路径长度为2的顶点:

(在上一步的基础上再往外走一步)

跟源点V3距离为2的顶点是V2和V4。

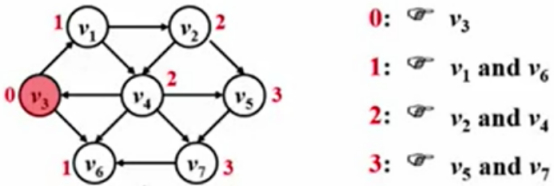
image.png

路径长度为3的顶点:

V2的邻接点V4已经被访问过，忽略，V5可以被访问。

V4的邻接点V6已经被访问过，忽略，V7可以被访问。

此时算法结束，这些顶点是一个个被收录进来，收录顺序是从V3的直接邻接点出发，一圈圈的往外扩展的，这个是广度优先搜索BFS。

image.png

(上述具体内容参考”案例过程”章节)

DIST:初始化时定义成一个特殊的字符或数字，在”案例过程”章节中定义成-1，表示未被访问过的结点，但初始结点S这里被设置成0，自己到自己的距离当然是0。

PATH:确认S到W经过的某个顶点。

关于时间复杂度T:由于不确定while和for的执行具体情况，所以不好确认。

换个角度，在整个算法执行过程中，每一个顶点只enqueue和dequeue了一次，所以整个过程中涉及了两倍的V，FOR的每个邻接点W，实际上就是把每条边访问了一次。

那么整体时间复杂度为|V|+|E|，涉及队列以及边的处理。

案例过程(O(|V|+|E|))

第1步:设置默认值

image.png

解释:

下标:每个结点都有一个下标值，在图中的实际位置。

距离:从源顶点到此顶点的实际距离，而不是某顶点到其邻接点的单一距离。

路径:父结点/顶点的下标值，默认全部-1。

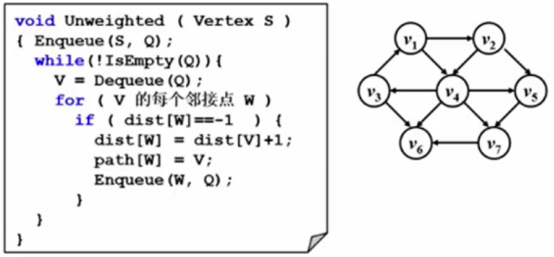
image.png

左边源码对应右边图形(下述描述结合步骤过程来看):

总体描述:

(1)初始化源顶点3。

(2)Enqueue(S,Q):源顶点3入队列，只执行一次。

(3)while和Dequeue(Q):队列出队一个结点V(也可以理解成被访问过了,右边图对应的结点圈变红色标记)。

(4)FOR:依次遍历结点V的所有邻接点，

(5)DIST[W]==-1:未被访问过DIST=-1，访问过不是-1，右边图对应的结点圈变红色标记，实际上是否访问过，实际上要看DIST是否等于-1，即DIST>0。

(5.1)DIST:

此邻接点W使用被遍历的V的DIST[下标]值，比如DIST[3]的实际值就对应下标为3的DIST值。

如果此V未被访问过，那么使用这个V的DIST[下标]+1。

比如在此案例中，V3的邻接点是V1和V6，那么此V6的DIST[6]=DIST[3]+1。

如果此V被访问过，那么此W的DIST值保持不变。

比如在此案例中，V4的邻接点有V5和V7，可是V5被V=V2时访问过，所以，这里的V5的DIST值保持不变。

(5.2)PATH:

此邻接点W使用被遍历的V的下标值，比如PATH[3]的实际值就对应V的下标值。

如果此V未被访问过，那么使用这个V的下标值。

比如在此案例中，V3的邻接点是V1和V6，那么此V6的PATH[6]=3。

如果此V被访问过，那么此W的PATH值保持不变。

比如在此案例中，V4的邻接点有V5和V7，可是V5被V=V2时访问过，所以，这里的V5的PATH值保持不变。

(5.3)Enqueue(W,Q):遍历的邻接点进队列，并为下次遍历此邻接点的其他所有邻接点。

另外:上述所有案例的内容，看下面的实际步骤内容。

第2步:起始结点3初始化

image.png

第3步:起始结点V3处理

开始调用Unweighted(Vertex S)函数，传入V3的下标3。

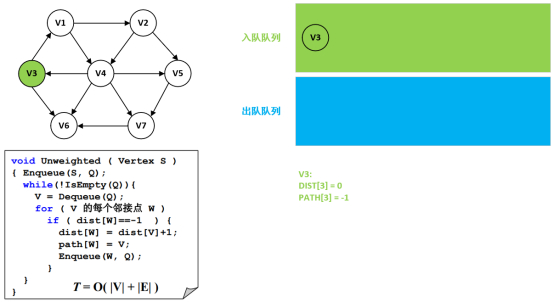
image.png

第4步:处理结点V3以及遍历邻接点V1和V6。

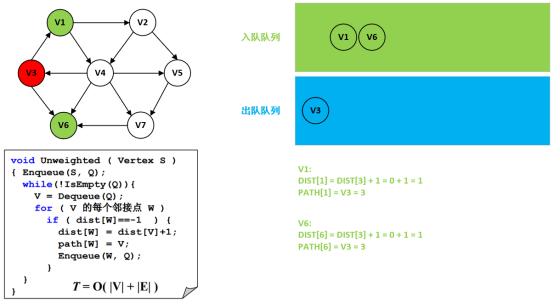
image.png

image.png

第5步:处理结点V1以及遍历邻接点V2和V4。

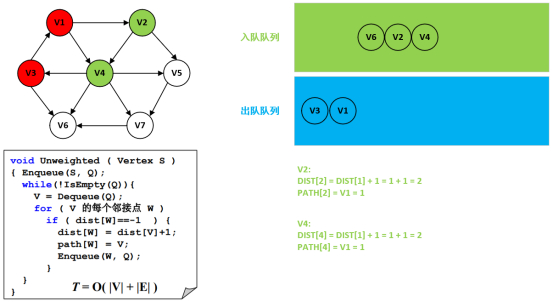
image.png

image.png

第6步:处理结点V6以及无可遍历的邻接点。

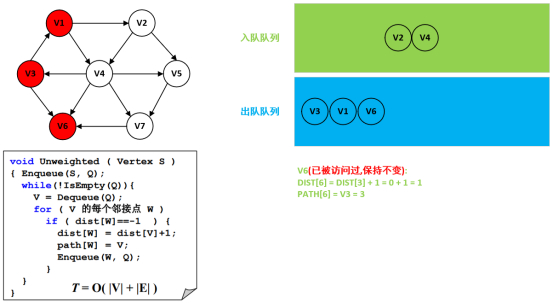
image.png

image.png

第7步:处理结点V2以及遍历邻接点V4和V5。

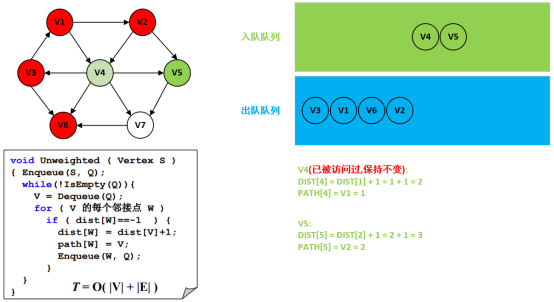
image.png

image.png

第8步:处理结点V4以及遍历邻接点V3、V5、V6、V7。

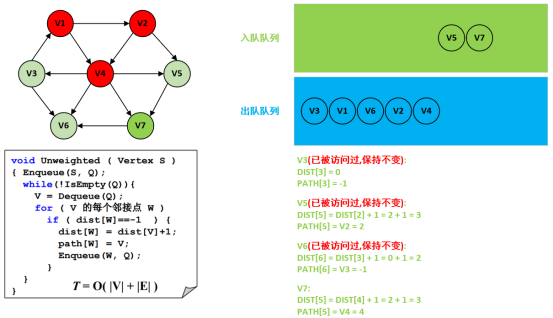
image.png

image.png

第9步:处理结点V5以及遍历邻接点V7。

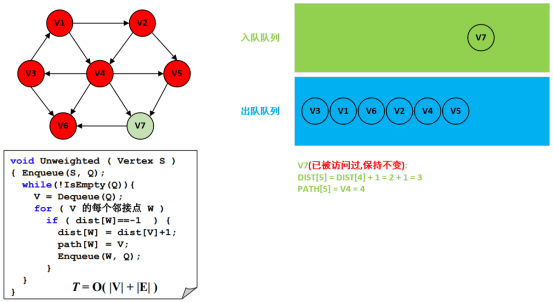
image.png

image.png

第10步:处理结点V7以及无可遍历的邻接点。

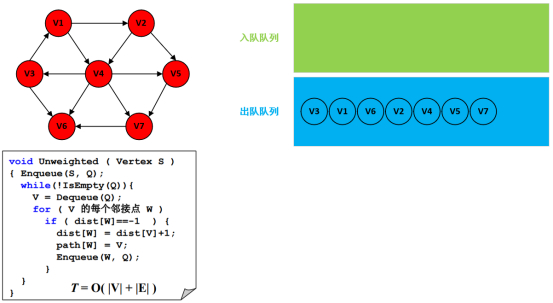
image.png

源码

#include<stdio.h>
/*
图-邻接表存储-无权图的单源最短路算法
*/
int main(void){
	return 0;
}
/* dist[]和path[]全部初始化为-1 */
void Unweighted(LGraph Graph, int dist[], int path[], Vertex S){
	Queue Q;
	Vertex V;
	PtrToAdjVNode W;
	/* 创建空队列, MaxSize为外部定义的常数 */
	Q = CreateQueue(Graph->Nv);
	/* 初始化源点 */
	dist[S] = 0;
	AddQ(Q, S);
	while(!IsEmpty(Q)){
		V = DeleteQ(Q);
		/* 对V的每个邻接点W->AdjV */
		for(W = Graph->G[V].FirstEdge; W; W = W->Next){
			/* 若W->AdjV未被访问过 */
			if(dist[W->AdjV == -1]){
				/* W->AdjV到S的距离更新 */
				dist[W->AdjV] = dist[V] + 1;
				/* 将V记录在S到W->AdjV的路径上 */
				path[W->AdjV] = V;
				AddQ(Q, W->AdjV);
			}
		}
	}
}

7.1.3 有权图的单源最短路径算法(Dijkstra)(邻接矩阵存储)

简介(有向有权图)

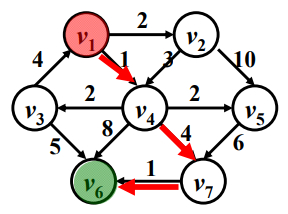
image.png

假定V1为源点，V6为终点，V1到V6这条路最短。

有权图的最短路与无权图的最短路很大的区别在于，有权图的最短路径不一定是经过顶点数最少的那条路。

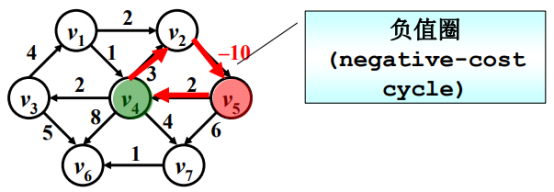
image.png

右边假如某条边为负数。

假定V5为源点，V4为终点的话，沿着红色箭头按着回路走，花2块钱、花3块钱、收10块钱，一圈净挣5块钱，只要不停的兜圈子，收入会无穷大，花销是负无穷大。

如果图中有这样一个负值圈，那么基本上所有的算法都会挂掉，后续讨论不会考虑这种情况。

(“负值圈”看”问题”章节)

image.png

有权图跟无权图的单源最短路径有一定相似之处，无权图其实是一个特殊的有权图，只不过每条边上的权重唯一就是了，所以它们的算法肯定有相似之处。

特点:按照递增的顺序或者非递减的顺序找出这个固定的源点到各个顶点的最短路径。

解决此问题的算法:Dijkstra算法。

image.png

Dijkstra算法其实跟广度优先搜索树BFS相似的地方在于把顶点一个个往集合中收。

定义一个顶点集合S，初始状态，只包括这个源点S，随着算法的进行，把一个个顶点不断收进来，收进来的顶点的最短路径都是已经确认的。

image.png

定义距离(权重)数组DIST，把DIST[V]定义为从源点到V的最短路径长度，但这并不是最短的路径长度，这个路径仅仅是从S到V中间经停的这个集合里面的顶点的这条路径的最小路径长度，所以并不是最终的最小路径长度。

随着顶点不断的被加入到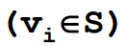image.png中，DIST[V]会慢慢变小，一直到最后被完善成为真正的最短路径长度，当DIST[V]成为真正的最短路径长度时，才会被收录到这个集合中，但是能执行的很重要的前提是路径是按照递增/非递减的顺序生成的，继续看下面。

image.png

当把V收录进去集合时，这个V真正的最短路径必须经过S里面的顶点，而不会经过S外面的顶点，为什么呢？

反证法。

比如从S到V，这条路径上存在另外一个结点W但是在S路径集合外的，

当从S到V，一定是S到W，再W到V就会有矛盾。

矛盾是，S到W的距离显然小于S到V的距离，而V是马上被收进集合中的顶点，而路径是按照递增顺序生成的，意味着比V要小的那些顶点应该在V之前都被收进去了，W到S的距离显然小于V到S的距离，所以W一定在集合里面，而不是在外面。

结论:真正的最短路径一定是经过S集合的顶点，可以没DIST数组中没被收进去的顶点收录到集合中。

image.png

把没有收录进集合的顶点中，选一个最小的DIST收录进集合中，这是贪心算法。

image.png

当把一个V收录进S集合中，是否会影响其他顶点的最小长度，这是一个很严重的问题。

如果收录V，使得S到W的路径变短，则:

S到W的路径一定经过V，但是V不一定直接跟W相连。

可以理解为:

如果把V加进去，这个W的距离变小的话，那么V一定在从S到W的路径上，V也应该是集合中距离最长的。

再者，从V到W必定存在一条直接的边，因为路径是按照递增的顺序生成的，所以不可能存在S->V->另外一个顶点->W。如果V到W之间还有一个顶点的话，那么这个顶点到源点的距离一定要比V到源点的距离要大。

可知，W一定是V的邻接点，V增加进集合后，影响的就是V一圈的邻接点，在程序中只要把V收进集合后，检查它的一圈邻接点，看有没有能得到一个更小的DIST值更新W的DIST值。

按照”案例过程”章节中自己理解的内容，

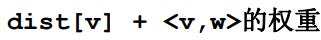image.png新路径长度，

image.png

旧路径长度，

如果新路径长度比旧路径长度要小，那么就更新W的DIST值，否则W的DIST值保持不变。

image.png

这里Dijkstra算法的DIST应该如何初始化？

如果S到W有直接的边，有直接相连的顶点，则DIST[V]=<S,W>的权重。

如果S到W没有直接的边，没有直接相连的顶点，则DIST[W]应该定义为”正无穷∞”。

(更多逻辑参考”案例过程”章节)

把DIST[W]定义为”正无穷∞”，这样当发现一个更短的路径的话，才可以把这个路径往更小的地方去更新，如果定义成-1的话，那么上述IF判断中DIST[W]的判断与更新就永远不会执行。

(“负边”情况看”问题”章节)

最后，当所有的顶点V都被收录到集合S中后，循环跳出不再执行。

关于整个算法的时间复杂度T，难点取决于上述伪代码标记的红色内容，”未收录顶点中dist最小者”以及”DIST最短路径的更新”，下述更多方法:

image.png

简单粗暴方法:直接扫描所有顶点，找到没收录的又是距离最小的O(|V|)。

因为所有的顶点都要被收录一次，外循环有V，内循环有V，涉及到每个顶点和边都被访问了一遍，跟E边数也是成正比的，所以T=O(|V|^2 + |E|)。

稠密图是有好多好多条边的，对于稠密图来说，实现效果比较好。

(“稠密图”看”问题”章节)

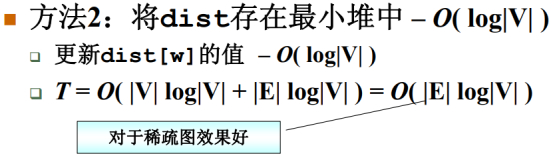
image.png

(“稀疏图”看”问题”章节)

这里E跟V是同一个数量级的，这里的复杂度比方法1中的O(|V|^2)要好些，如果这个图充分稀疏的话，那么用一个最小堆实现Dijkstra算法会得到更快的效果。

案例过程(稠密图:O(|V|^2+|E|),稀疏图:O(|E|Log|V|))

第1步:设置默认值

image.png

解释:

下标:每个结点都有一个下标值，在图中的实际位置。

权重:从源顶点到此顶点的实际距离，而不是某顶点到其邻接点的单一距离，默认正无穷。

路径:父结点/顶点的下标值，默认全部-1。

image.png

左边源码对应右边图形(下述描述结合步骤过程来看):

总体描述:

(1)初始化起始结点V1和邻接点V2、V4。

初始化两个数组:权重DIST和存储路径PATH。

(2)选择编号V1作为源点，相应的源点到V1自己的距离/权重DIST默认0。

那么，V1的邻接点V2和V4到V1的距离/权重DIST分别为2和1。

此邻接点V2和V4使用被遍历的V1的下标值，比如PATH[2]和PATH[4]的实际值就对应V的下标值V1=1。

V1结点是默认被访问过的，那么右边图形就要默认标红，对应上述源码中collected[V] = true。

(3)Dijkstra(Vertex S):源顶点V1入队列，只执行一次。

(4)while(1)进入循环。

(5)V=”未收录顶点中dist最小者”，即:找除访问过的顶点外，距离源点V1距离最近的顶点。

比如，在初始化时，”未访问过的顶点并且距离源点V1最近的顶点”是V2和V4。

(6)collected[V] = true;设置上述步骤中的某个结点是被访问过的，那么在右边图中，被标红。

比如，V2和V4，V4距离源点V1距离最近，设置collected[V4] = true。

(7)FOR:依次遍历(5)中选择某个结点V的所有邻接点W集合,比如V4的邻接点有V3、V5、V6、V7。

(5)collected[W]=false:未被访问过collected=false，访问过是true，右边图对应的结点圈变红色标记，比如collected[V3]=false。

(6)if(DIST[V] + E(v,w)) < DIST[W]

可以把if(DIST[V] + E(v,w))当成新路径及新距离，可以把DIST[W]当成原路径及原距离。

DIST[V]指访问结点的权重值。

E(v,w)指访问结点到现在邻接点的权重值，路径为V->W。

比如V=V4，W=V3。

DIST[V] + E<v,w>为DIST[V4] + E(V4->V3) = 1 + 2 = 3。

DIST[W]为DIST[V3] = ∞。

此时，3 < ∞。

(7)满足(6)的条件再执行。

DIST[W] = DIST[V] + E<v,w>。

PATH[W] = V。

比如V=V4，W=V3。

DIST[3] = DIST[4] + E<V4,V3> = 1 + 2 = 3。

PATH[3] = V4 = 4。这里的PATH值就等于这里处理结点V的下标值。

上述二者更新到DIST和PATH数组中。

第2步:起始结点V1和邻接点V2、V4初始化

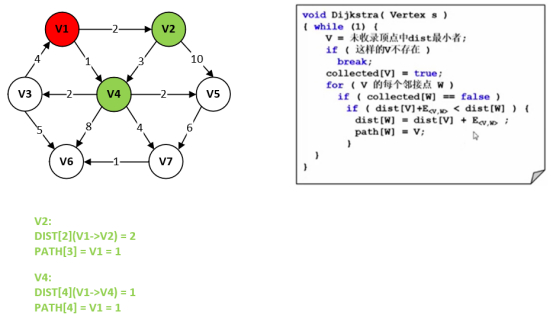
image.png

image.png

第3步:起始结点V1处理V2和V4中的V4

开始调用Dijkstra(Vertex S)函数，传入V1的下标1。

此时，”未收录顶点中的dist最小者”，为V1的邻接点V2和V4，其中V4距离V1距离最小，下述先开始执行V4。

第4步:处理结点V4以及遍历邻接点V3、V5、V6、V7。

image.png

image.png

第5步:处理结点V2以及遍历邻接点V4、V5。

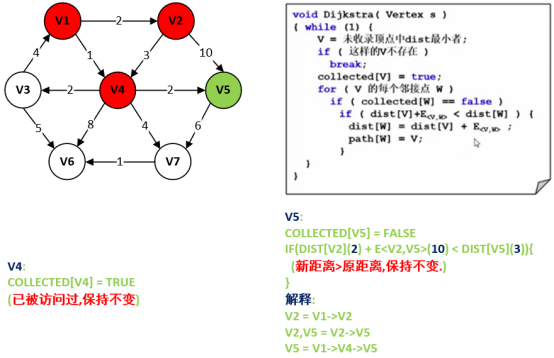
image.png

image.png

第6步:找未收录顶点中dist的最小者,距离源点V1最近的顶点。

在DIST数组中，现阶段符合条件的有V3、V5，其中V3和V5最小，DIST都相等，那么这里选择编号最小的V3。

第7步:处理结点V3以及遍历邻接点V1、V6。

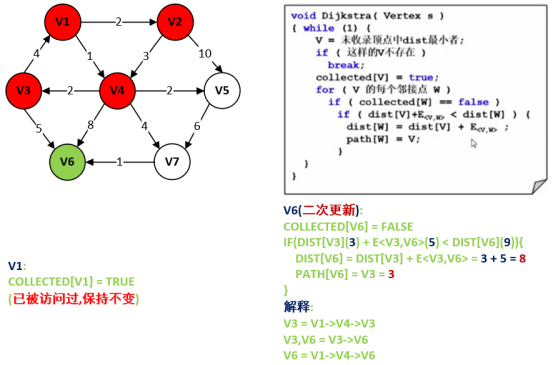
image.png

image.png

注意: 结点6为二次更新 。

第8步:处理结点V5以及遍历邻接点V7。

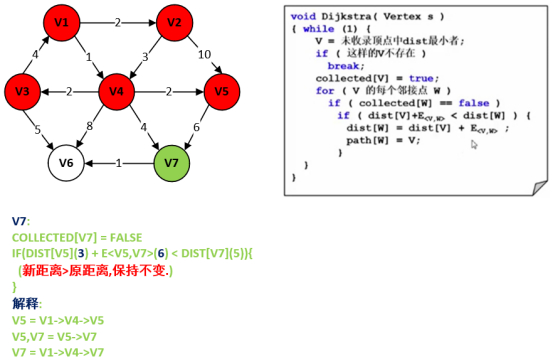
image.png

image.png

第9步:找未收录顶点中dist的最小者,距离源点V1最近的顶点。

在DIST数组中，现阶段符合条件的有V6、V7，其中V7最小，那么这里选择最小的V7。

第10步:处理结点V7以及遍历邻接点V6。

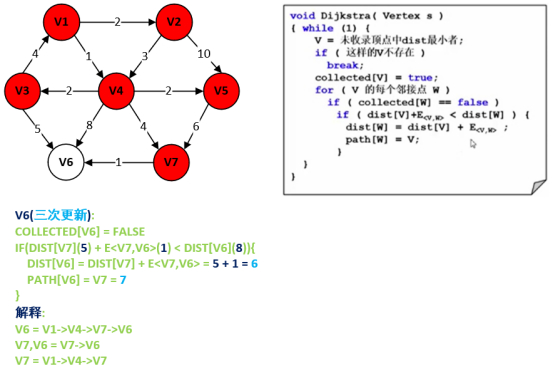
image.png

image.png

注意: 结点6为三次更新 。

第11步:处理结点V6。

除了V6，图中没有再可以访问的顶点，且V6也没有可再访问的邻接点。

跳出循环。

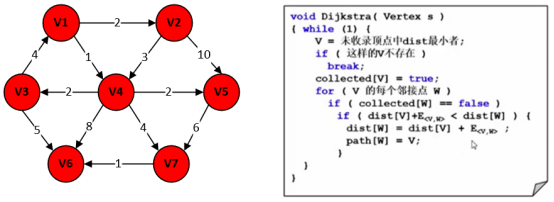
image.png

image.png

另外:处理源点V1到终点V6的最短路径。

image.png

那么这条最短路径为:V1->V4->V7->V6。

最终每个顶点的最短路径与权重DIST和路径PATH的关系:

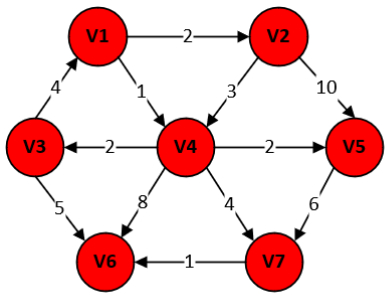
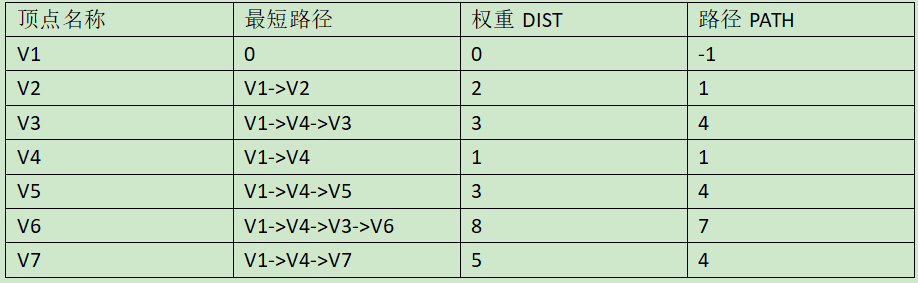
image.png

image.png

7.1.4 多源最短路径 算法 (Floyd)(邻接矩阵存储)

简介(无向有权图)

image.png

image.png

对于稠密图，比较友好，它的每条最短路径不是一次性成型的，是逐步成型的。

image.png

定义的二维数组也就是矩阵，D[i][j]定义的是从i到j最短路径长度，只经过小于等于K的顶点。

image.png

比如顶点编号从0开始，一直编码到V-1，当K=V-1时，那么此路径就是最短路径了。

image.png

image.png

image.png

第1种可能，新的顶点K不在集合中，那就没必要更新路径了。

第2种可能，新的顶点K在集合中，影响了i到j之间的最短路径，K一定在i到j的最短路径上，这段路径一定是两段组成的，从i到K，从K到j，但是都不包括顶点K？？？？

从i到j之间的最短路径三部分构成:i->k,k,k->j。

(看”问题”章节)

image.png

源码(稠密图Floyd:O(|V|^3),稀疏图:O(|V|^3+|E|*|V|))


#include<stdio.h>
/*
图-邻接矩阵存储-多源最短路(Floyd)算法
*/
int main(void){
	return 0;
}

bool Floyd(MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum]){

	Vertex i,j,k;

	/* 初始化 */
	for(i = 0; i < Graph->Nv; i++){

		for(j = 0; j < Graph->Nv; j++){
			/*
			邻接矩阵初始化
			*/
			D[i][j] = Graph->G[i][j];
			/*
			输出ij之间的最短路径.
			-1表示ij之间现在是没有路径的.
			*/
			path[i][j] = -1;
	
		}

	}
	/*
	跟着k从0开始一步步的向后推
	*/
	for(k = 0; k < Graph->Nv; k++){
		for(i = 0; i < Graph>Nv; i++){
			for(j = 0; j < Graph->Nv; j++){
				/*
				计算ij之间的最短距离:i->k->j
				*/
				if(D[i][k] + D[k][j] < D[i][j]){
					/*
					更新ij之间的最短距离:i->k->j
					i和j之间一定会经过k
					*/			
					D[i][j] = D[i][k] + D[k][j];
					/* 若发现负值圈 */
					if(i == j && D[i][j] < 0){
						/* 不能正确解决，返回错误标记 */
						return false;
					}
					/*
					输出ij之间的最短路径
					三段路径组成:i->k,k,k->j
					*/
					path[i][j] = k;
				}
			}
		}
	}

	return true;

}

案例过程( 哈利•波特的考试 )

题意理解

image.png

把猫变成老鼠，咒语haha，4个字符，权重。

把老鼠变成鲨鱼，咒语hehe，4个字符，权重。

把猫直接变成鲨鱼，咒语lalala，6个字符，权重。

这是一个无向图。

如果一个人要带一个动物出去，带哪个去比较核算，路径最短呢？

对猫来说，最难变的动物是鲨鱼，反过来，同理，路径长，都需要6个字符。

但是，对于老鼠来说，变猫还是鲨鱼都是4个字符，反过来同理，最简单，路径最短。

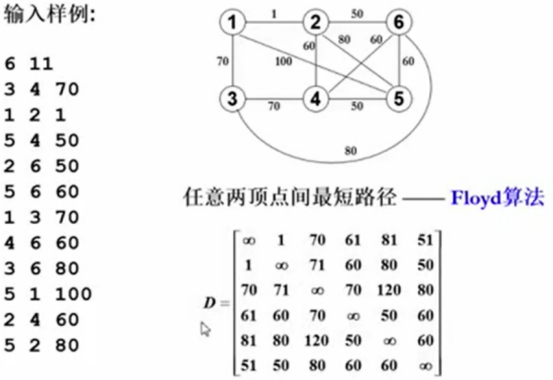
image.png

左边数字。

6顶点个数，动物个数。

11边的个数。

右上角，无向图，

使用Floyd算法找出任意两个顶点之间最短的路径。

矩阵D(i,j)记录的是从顶点i到顶点j之间最短的距离。

可以发现，每个坐标的值，标记的都是两个顶点之间最短的距离，即权重。

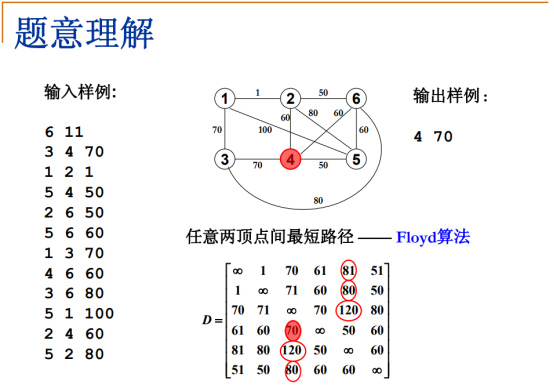
image.png

动物的编号是从1开始的，带哪只动物出去，用Floyd算法去算任意两个顶点之间的最短路径，步骤:

第一步:

对每个顶点扫描，扫描其他所有顶点(每个顶点和其他所有顶点之间)最短路径的最大值，这里检查每一行(每个顶点和其他所有顶点的距离集合)里面最大的数字。

第1行/第1个动物-最大值:D(1,5)=81，顶点1到顶点5最短距离81。

第2行/第2个动物-最大值:D(2,5)=80，顶点2到顶点5最短距离80。

第3行/第3个动物-最大值:D(3,5)=120，顶点3到顶点5最短距离120。

第4行/第4个动物-最大值:D(4,3)=70，顶点4到顶点3最短距离70。

第5行/第5个动物-最大值:D(5,3)=120，顶点5到顶点3最短距离120。

第6行/第6个动物-最大值:D(6,3)=80，顶点6到顶点3最短距离80。

第二步:

在第一步中得到所有顶点的最大值集合中的最小值，这里是70，这就是任意两个顶点之间最短的路径。

源码

#include<stdio.h>
/*
图-邻接矩阵存储-多源最短路(Floyd)算法-哈利波特
*/
int main(void){
	/*
	读入图
	*/
	MGraph G = BuildGraph();
	/*
	分析图
	*/
	FindAnimal(G);
	return 0;
}
/* 最大顶点数设为100 */
#define MaxVertexNum 1000
/* ∞设为双字节无符号整数的最大值65535*/
#define INFINITY 65535
/* 用顶点下标表示顶点,为整型 */
typedef int Vertex;
/* 边的权值设为整型 */
typedef int WeightType;
/* 顶点存储的数据类型设为字符型 */
/*
顶点不存储数据,所以这里不声明.
typedef char DataType;
*/

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
	/* 有向边<V1, V2> */
	Vertex V1, V2;
	/* 权重 */
	WeightType Weight;
};
typedef PtrToENode Edge;
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
	/* 顶点数 */
	int Nv;
	/* 边数 */
	int Ne;
	/* 邻接矩阵 */
	WeightType G[MaxVertexNum][MaxVertexNum];
	/* 存顶点的数据 */
	/* 注意：很多情况下，顶点无数据，此时Data[]可以不用出现 
	DataType Data[MaxVertexNum]; 
	*/
};
/* 以邻接矩阵存储的图类型 */
typedef PtrToGNode MGraph;

/*
读入并建立图
*/
MGraph BuildGraph(){
	MGraph Graph;
	Edge E;
	/*
	不需要
	Vertex V;
	*/
	int Nv, i;
	/* 读入顶点个数 */
	scanf("%d", &Nv);
	/* 初始化有Nv个顶点但没有边的图 */
	Graph = CreateGraph(Nv);
	/* 读入边数 */
	scanf("%d", &(Graph->Ne));
	/* 如果有边 */
	if(Graph->Ne != 0){
		 /* 建立边结点 */
		 E = (Edge)malloc(sizeof(struct ENode));
		 /* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
		 for(i = 0; i < Graph->Ne; i++){
		 	scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
		 	/*
			图插入边时,顶点编号从0开始,
			在输入读入边时,顶点编号从1开始,所以每个顶点做-1操作.
			因为是无向图,把权重互相
			*/
		 	/* 起始编号从0开始 */
		 	E->V1--;
		 	E->V2--;
		 	/*
			插入边 
			*/
		 	InsertEdge(Graph, E);
		 }
	}
	/* 如果顶点有数据的话，读入数据 */
	/*
	这里顶点没数据不处理
	for(V=0; V<Graph->Nv; V++){
		scanf(" %c", &(Graph->Data[V]));
	}
	*/
	return Graph;
}

/* 
初始化一个有VertexNum个顶点但没有边的图 
*/
MGraph CreateGraph(int VertexNum){
	Vertex V, W;
	MGraph Graph;
	/* 建立图 */
	Graph = (MGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
	/* 初始化邻接矩阵 */
	/* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
	for(V = 0; V < Graph->Nv; V++){
		for(W = 0; W < Graph->Nv; W++){
			Graph->G[V][W] = INFINITY;
		}
	}
	return Graph;
}

/*
插入边 
*/
void InsertEdge(MGraph Graph, Edge E){
	/* 插入边 <V1, V2> */
	Graph->G[E->V1][E->V2] = E->Weight;
	/* 若是无向图，还要插入边<V2, V1> */
	Graph->G[E->V2][E->V1] = E->Weight;
}


/*
分析图
*/
void FindAnimal(MGraph Graph){

	WeightType G[MaxVertexNum][MaxVertexNum], MaxDist, MinDist;
	Vertex Animal, i;
	/*
	多源最短路径算法Floyd
	*/
	Floyd(Graph, D);
	/*
	从这里到最后printf:
	从每个动物i顶点的最短距离(其他所有动物顶点集合)的最大值中,
	找到最小值MinDist,以及对应的动物Animal.
	得到矩阵D.
	*/
	/*
	初始化最短距离
	*/
	MinDist = INFINITY;
	/*
	扫描第i行的数据,在FindMaxDist中扫描第i行的动物顶点和第某i行对应的第j列集合的所有顶点
	*/
	for(i = 0; i < Graph->Nv; i++){
		/*
		从一堆数据中找一个最大值.
		MaxDist在方法中是从0开始.
		*/
		MaxDist = FindMaxDist(D, i, Graph->Nv);
		/* 
		说明有从i无法变出的动物 .
		特殊情况:带一只动物根本不可能.
		图不止一个连通集,当图根本不连通的时候,所以带一只动物去是不可能的.
		当返回MaxDist为INFINITY无穷大的话,说明从动物i到其他动物的最大距离是无穷大,
		意味着从i开始,至少存在一个动物无法变出来,直接return回去.
		*/
		if(MaxDist == INFINITY){
			printf("0\n");
			return;
		} 
		/* 找到最长距离更小的动物 */
		if(MinDist > MaxDist){
			MinDist = MaxDist;
			/* 更新距离,记录编号,而声明动物的编号是从1开始,i初始为0,所以+1. */
			Animal = i + 1;
		}
	}
	/*
	输出动物编号和最小距离.
	*/
	printf("%d %d\n", Animal, MinDist);
}


/*
多源最短路径算法Floyd
*/
void Floyd(
/*
bool Floyd(
*/
			/*
			计算两个顶点之间的距离
			*/
			MGraph Graph, WeightType D[MaxVertexNum]
			/*
			不需要计算两个顶点之间的路径
			Vertex path[][MaxVertexNum]
			*/
			){

	Vertex i, j, k;
	/* 初始化 */
	for(i = 0; i < Graph->Nv; i++){
		for(j = 0; j < Graph->Nv; j++){
			D[i][j] = Graph->G[i][j];
			/*
			不需要计算两个顶点之间的路径
			path[i][j] = -1;
			*/
		}
	}

	for(k = 0; k < Graph->Nv; k++){
		for(i = 0; i < Graph->Nv; i++){
			for(j = 0; j < Graph->Nv; j++){
				if(D[i][k] + D[k][j] < D[i][j]){
					D[i][j] = D[i][k] + D[k][j];
					/*
					在此题目中,输入的所有距离都是正数,所以此判断不需要,会一直返回true,也不需要bool布尔返回类型.
					若发现负值圈
					if(i == j && D[i][j] < 0){
						不能正确解决，返回错误标记
						return false;
					}
					*/
					/*
					不需要计算两个顶点之间的路径
					path[i][j] = k;
					*/
				}
			}
		}
	}

	/*
	为何最初返回bool布尔值?
	正常情况返回true表示正常结束返回true.
	当出现负值圈的时候表示非正常结束返回false.
	负值圈意味着从i出发又回到了i,这个最短距离是负值是不能正常往下运行Floyd算法的.
	return true;
	*/
}
/*
从一堆数据中找一个最大值
*/
WeightType FindMaxDist(WeightType D[][MaxVertexNum], Vertex i, int N){

	WeightType MaxDist;
	Vertex j;
	/*
	从一堆数据中找一个最大值的诀窍:把这个MaxDist初始化成很小的数.
	*/
	MaxDist = 0;

	/* 找出某动物i(固定值)顶点到其他所有动物j顶点集合中的最长距离,第 */
	for(j = 0; j < N; j++){
		if(
			/*
			对角元:邻接矩阵,最开始的时候所有两个顶点之间的距离全部初始化为正无穷,
			此时,如果不把对角元排除的话,那么当读到对角元的时候,肯定大于MaxDist,
			那么这个MaxDist就会永远返回正无穷,所以在比较之前加下述"i!=j"的判断就把对角元跳过去了.
			*/
			i != j 
			&& 
			/*
			如果某个D[i][j]比已经找到的最大距离还大,那么更新此i的最大距离.
			*/
			D[i][j] > MaxDist){
	
			MaxDist = D[i][j];
	
		}
	}

	return MaxDist;
}
标题：(数据结构)第七讲-图(7.1 最短路径问题)
作者：yazong
地址：https://blog.llyweb.com/articles/2023/10/22/1697964135485.html