9.2 希尔排序 (对比插入排序)

希尔排序是Donald Shell这个人在1959年提出，基本思路:利用插入排序的简单，同时要克服插入排序每次只交换相邻两个元素的缺点。

间隔排序(不破坏上步排序结果)

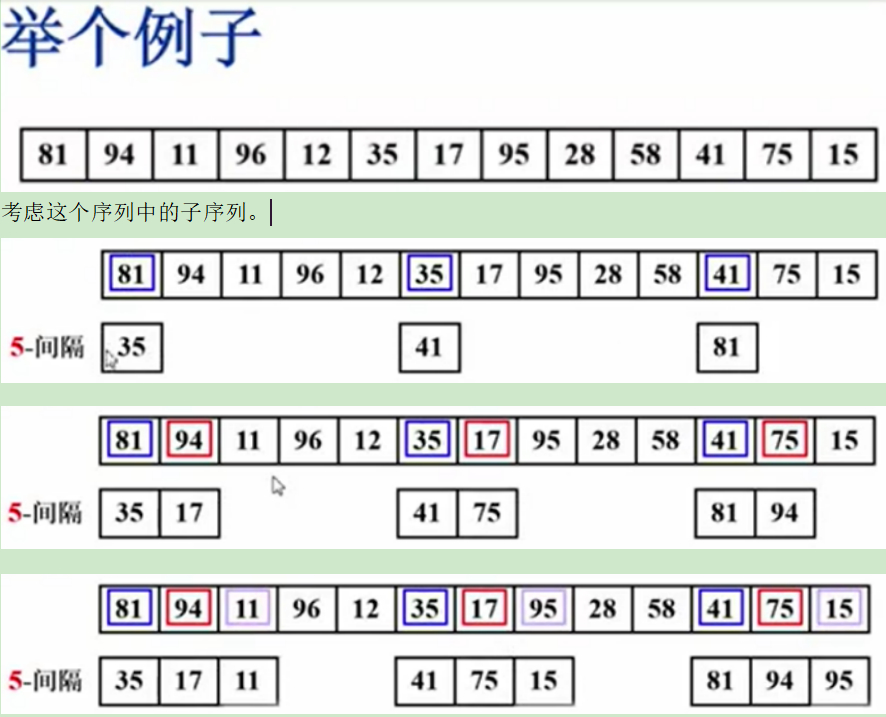
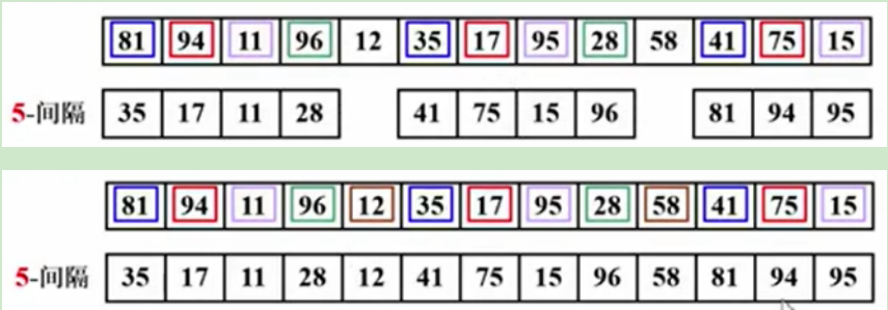
5-间隔:子序列每隔5个元素来选取，利用插入排序，再排序，其他同理，排序完，元素之间的间隔变小了一些。

下述3-间隔以5-间隔的结果接着排序。

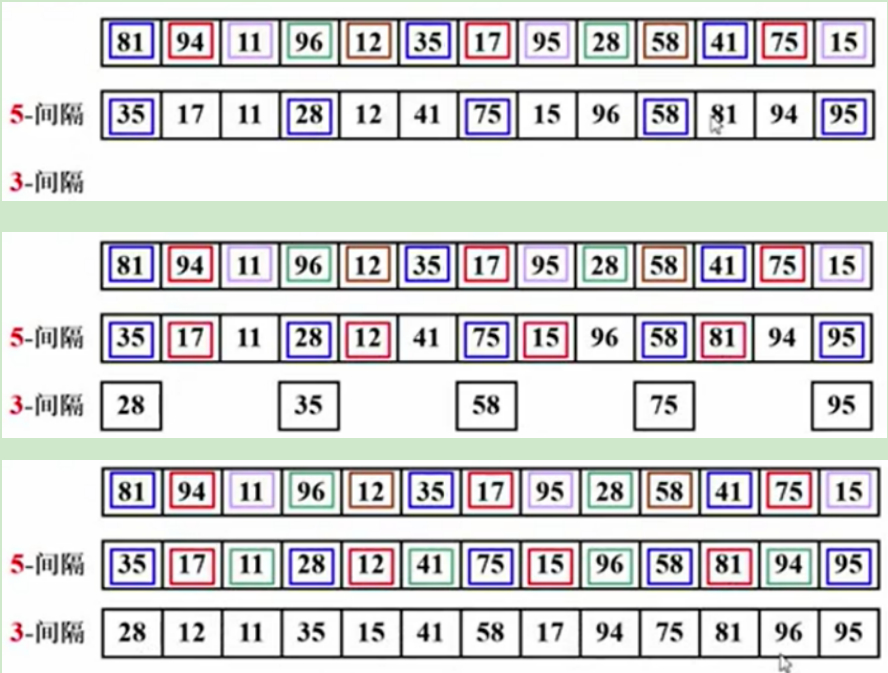
3-间隔:此排序结果，有了非常明显的改善。最后要保证这个序列有序的话，还是要做1-间隔的步骤。

下述1-间隔以3-间隔的结果接着排序。

1-间隔:这里做的是彻底的插入排序。可以发现在做1-间隔的原始插入排序之前，此3-间隔的序列已经基本有序了，因为大部分的逆序对在前面的两趟排序中已经被销掉了。

主要思想:先定义一个增量序列，也可以定义自己的。

从某个数字开始，几间隔，无论如何这个序列他是递减的，递减到最小的1间隔。

定义增量序列后，对每一个增量进行增量间隔的排序，K是从M开始一直减到1为止。

有一个很重要的性质，当对这个序列先进行了5-间隔的插入排序，再进行3-间隔的插入排序，那么，3-间隔的插入排序以后，这个序列还是5-间隔的有序序列。

比如3-间隔后，28隔五个数是41，再隔五个数是81，它们三个是有序的，那么3-间隔有序的序列还保持了5-间隔有序的这个性质，比如1-间隔看3-间隔的序列数据同理。

更小间隔的排序，并没有把上一步的结果变坏，这是一个非常重要的性质，否则希尔排序就不好用了。

增量序列(N/2逐渐减半-O(N^2))

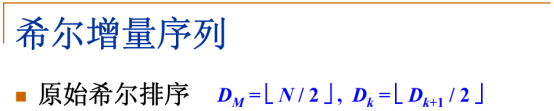
增量序列的选择:开始取N/2，每次把增量/2每次减半，最后减到1为止。

/*
原始希尔排序-伪代码
增量序列的选择:开始取N/2，每次把增量/2每次减半，最后减到1为止。
时间复杂度-最坏情况:T = Θ(N^2)，达不到上界O(N^2)，Ω是下界，也就是说，Θ既是上界又是下界，增长速度跟N^2一样快。
源码中的D可对照插入排序中的1，这里可以理解把把插入排序中的1都替换成了D。
*/
void Shell_sort(ElementType A[], int N){

	/* 希尔增量序列 */
	for(D = N/2; D > 0; D/=2){
		/* 插入排序 */
		for(P = D; P < N; P++){
			Tmp = A[P];
			for(i = P; i >= D && A[i - D] > Tmp; i-=D){
				A[i] = A[i - D];
			}
			A[i] = Tmp;
		}
	}

}

增量序列(增量元素互质-小增量起作用)

时间复杂度如此之差，问题出在哪里呢？

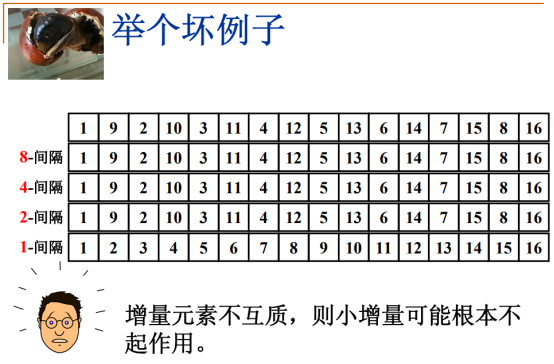
先做8-间隔，第二次间隔8个，数7个后面就没有了，发现本来就是有序的。

4-间隔和2-间隔同理。

要达到有序还要靠1-间隔。

前面白做了三趟排序，最后跟原始的插入排序结果一样。

比如8421这类小的增量就有可能在后面的排序中不起作用。

为克服此问题，有更多的学者提出了更多的增量序列。

更多增量序列(Hibbard+Sedgewick)

(1.1)此增量序列的好处，保证了相邻的元素是互质的，互质意思是说相邻的两个元素之间没有公因子，希尔排序用Hibbard增量训练会好一些。

(1.2)此次方如何得到很困难，略。

(1.3)此次方到现今为止没有人能证明，可能是这个结果。

(2)到现今为止没有人能证明出来，如果要排序的元素的数量是几万数量级的，那么用希尔排序+Sedgewick增量序列是比较好的。

源码(高于堆排序):Sedgewick增量序列+插入排序

/*
希尔排序-用Sedgewick增量序列(+插入排序)
*/
void ShellSort(ElementType A[], int N){

	int Si, D, P, i;
	ElementType Tmp;
	/* 这里只列出一小部分增量 */
	int Sedgewick[] = {929, 505, 209, 109, 41, 19, 5, 1, 0};
	for(Si = 0; Sedgewick[Si] >= N; Si++);
	/* 初始的增量Sedgewick[Si]不能超过待排序列长度 */
	for(D = Sedgewick[Si]; D > 0; D = Sedgewick[++Si]){
		/* 插入排序*/
		for(P = D; P < N; P++){
			Tmp = A[P];
			for(i = P; i >= D && A[i - D] > Tmp; i-=D){
				A[i] = A[i - D];
			}
			A[i] = Tmp;
		}
	}
}