9.3.1 选择排序 (Θ(N^2) )

#include<stdio.h>
/*
排序
*/
int main(void){
	return 0;
}
/*
排序-选择排序-时间复杂度(T = Θ(N^2))
*/
void Selection_sort(ElementType A[], int N){

	for(i = 0; i < N; i++){
		/*
		从A[i]到A[i - 1]中找到最小元,并将其位置赋给MinPosition.
		这里是瓶颈.
		选择排序最简单粗暴的方法:从A[i]到A[i - 1]每次都扫描一遍,把最小元记录到A[i]中去.
		ScanForMin对应的也是一个循环,外头又套了一层循环,那么时间复杂度(T = Θ(N^2)).
		*/
		MinPosition = ScanForMin(A, i, N - 1);
		/*
		将未排序部分的最小元换到有序部分的最后位置.
		有序部分的最后位置就是i这个位置.
		下述的两个元素在大多数情况下不是挨着的,可能跳了很远的距离做了一个交换,那么这一次的交换就是一个好消息,
		我们可能就一次交换就消掉了很多的逆序对,其实对于这个选择排序而言,最坏情况下每次都要换一次,
		最多换N-1次,最后一个元素不用换,交换这部分时间的复杂度是线性的O(N).
		*/
		Swap(A[i], A[MinPosition]);
	}

}

9.3.2 堆排序 (最小元)

堆的元素是从第一个下标为1的元素开始计数的，A[0]是不放任何真元素的，而是放的哨兵，而在排序的算法中，用户并不知道应该在前面留个哨兵元素，用户是从第0个元素就开始存在的，所以堆中的元素也是从0开始记的，这就导致了任何一个结点跟它的孩子结点的下标关系就不同了。

那么在堆排序中，元素下标从0开始，则对于下标为i的元素，左孩子的下标为2i+1，右孩子的下标为2i+2。

(对比5.1和9.3)

源码:堆排序-未优化( O(NLogN) )

/*
排序-堆排序-算法1-未优化
时间复杂度:T(N) = O(NLogN)
需要额外O(N)的空间,并且复制元素需要时间.
*/
void Heap_Sort(ElementType A[], int N){
	/* 线性时间复杂度O(N) */
	BuildHeap(A);
	for(i = 0; i < N;i++){
		/* 
		O(LogN)加上外循环就是O(NLogN) 
		弹出根结点,弹出来之后开辟临时数组TmpA存放数据,要需要把这个临时数组TmpA中的数据倒回A数组中去.
		*/
		TmpA[i] = DeleteMin(A);
	}
	for(i = 0; i < N;i++){
		/* 
		O(N) 
		如果内存是2GB，可以对2GB的数据进行排序，因为要开额外的空间A[i] = TmpA[i]，
		导致一次只能排1GB的内容，复制元素也是需要占据空间的。
		*/
		A[i] = TmpA[i];
	}
}

案例:堆调整排序(左孩子下标:2i+1-右孩子下标2i+2)

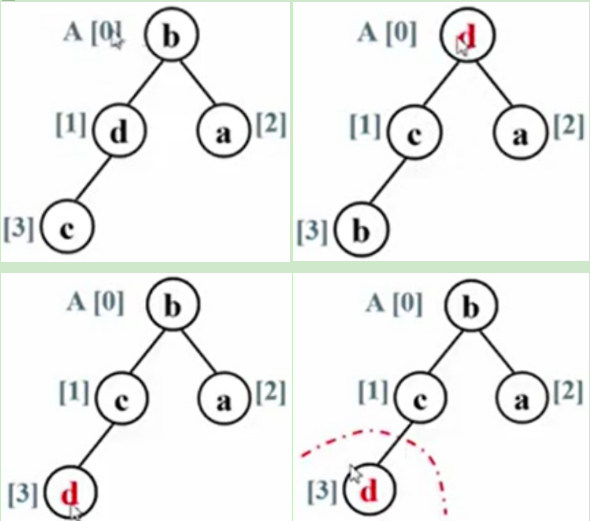
(1)调整最大堆:先把最小堆调整成最大堆，B和D换位置；

(2)堆排序循环:在一个正常排好序的数组中，最大元素应该放在最后一个位置，要把根结点与最后一个结点换位置，D下来，B上去；

(3)剩余/当前元素调整最大堆(调整时以0为根结点):堆的规模-1，D就排除在外，D已经在其正确位置上了，无论后面再做什么这个D都不用动了。

(2)和(3)其实可以合并起来说。

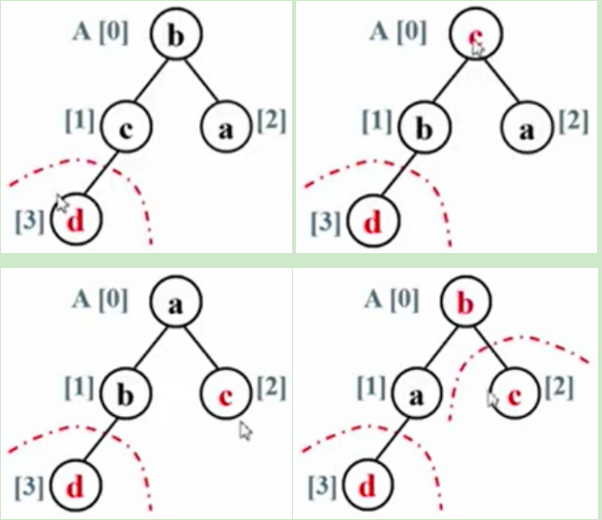
重复上述步骤。

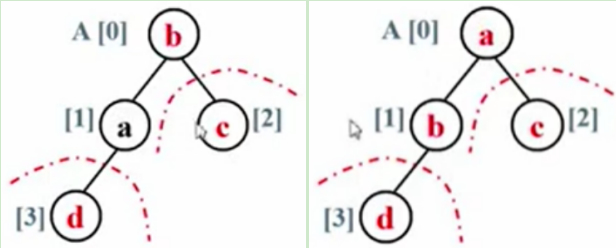
现在堆中只剩下A和B两个元素。

B和A做最后一次交换。

此时完成排序。

堆的元素是从第一个下标为1的元素开始计数的，A[0]是不放任何真元素的，而是放的哨兵，而在排序的算法中，用户并不知道应该在前面留个哨兵元素，用户是从第0个元素就开始存在的，所以堆中的元素也是从0开始记的，这就导致了任何一个结点跟它的孩子结点的下标关系就不同了。

那么在堆排序中，元素下标从0开始，则对于下标为i的元素，左孩子的下标为2i+1，右孩子的下标为2i+2。

(对比5.1和9.3)

随机排列:平均比较次数-平均时间复杂度

源码:堆排序-优化(低于希尔排序-Sedgewick增量序列)

/*
排序-堆排序-真正的堆排序-伪代码
把BuildHeap函数编写的更具体一些.
*/
void Heap_Sort2(ElementType A[], int N){

	/*
	反复调用就把一个最大堆建立起来了.
	*/
	for(i = N/2-1; i >= 0; i--){
		/*
		核心调用向下过滤函数
		i根结点所在位置.
		N当前这个堆里一共有多少个元素.
		*/
		ParcDown(A, i, N);
	}
	/*
	堆排序的循环
	当上述最大堆建立起来后,A[0]根结点存的一定是最大的元素.
	i存的是当前的最后一个元素它的下标.
	*/
	for(i = N-1; i > 0; i--){
		/*
		把根结点换到当前这个堆的最后一个元素的位置上去.
		*/
		Swap(&A[0], &A[i]);
		/*
		继续把剩余的元素调整成一个最大堆.
		调整时以0为根结点,
		i是当前这个最大堆的元素的个数.
		*/
		PercDown(A, 0, i);
	}

}
/*
元素交换
*/
void Swap(ElementType *a, ElementType *b){
	ElementType = *a;
	*a = *b;
	*b = t;
}
/*
调整最大堆-根据5.1改造
将N个元素的数组中以A[p]为根的子堆调整为最大堆.
*/
void PercDown(ElementType A[], int N){

	int Parent, Child;
	ElementType X;

	/* 取出根结点存放的值 */
	X = A[p];
	for(Parent = p; (Parent * 2 + 1) < N; Parent = Child){
		Child = (Parent * 2 + 1);
		if((Child != N - 1) && (A[Child] < A[Child + 1])){
			/* Child指向左右子结点的较大者 */
			Child++;
		}
		if(X >= A[Child]){
			/* 找到了合适位置 */
			break;
		}else{
			/* 下滤X */
			A[Parent] = A[Child];
		}
	}
	A[Parent] = X;

}

/* 
堆排序 
*/
void HeapSort(ElementType A[], int N){
	int i;
	for(i = N/2-1; i >= 0; i--){
		/* 建立最大堆 */
		PercDown(A, i, N);
	}
	for(i = N - 1; i > 0; i--){
		/* 删除最大堆顶 */
		Swap(&A[0], &A[i]);
		/* 根据当前元素建立最大堆 */
		PercDown(A, 0, i);
	}
}