9.4.1 有序子列的归并 (核心基石-O(N))

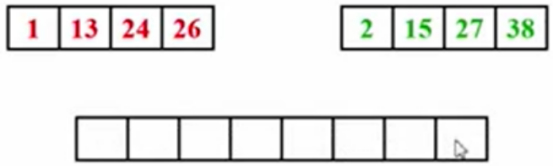
假设两个子序列本身是已经排好序的，目标是另外开设一个数组，把这些数字一个个放到数组中去，并且希望这个数组是从小到大排序的。

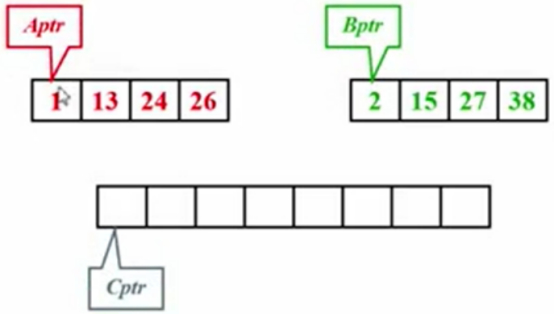
跟线性表章节中两个多项式相加的想法类似。

AB俩指针分别指向两个子序列的两个元素，C指针指向数组，AB指向的两个元素谁小，就放到C指针的位置上。

A指针指向的小，放到C指针的位置。A指针和C指针都挪动指针到下一个位置。以后同理。

那么，如果两个子列一共有N个元素，那么这一趟归并(每个元素被扫描了一遍,每个元素被存进来一次)的时间复杂度T(N)=O(N)。

/*
有序子列的归并-根据案例图看源码
如果两个子列一共有N个元素，那么这一趟归并(每个元素被扫描了一遍,每个元素被存进来一次)的时间复杂度T(N)=O(N).
*/
/* 
ElementType A[]原始待排序列
ElementType TmpA[]临时数组,存储归并以后的结果.
L = 要合并的左边起始位置
R = 要合并的右边起始位置
RightEnd = 右边终点位置 
*/
void Merge(ElementType A[], ElementType TmpA[], int L, int R, int RightEnd){

	/* 左边终点位置。假设左右两列挨着 */
	LeftEnd = R - 1;
	/* 存放结果的数组的初始位置 */
	Tmp = L;
	/*归并完成后中间元素的总个数*/
	NumElements = RightEnd - L + 1;
	/*
	L小于等于左边终点R小于等于右边终点
	*/
	while(L <= LeftEnd && R <= RightEnd){
		if(A[L] < A[R]){
			TmpA[Tmp++] = A[L++];
		}else{
			/*不为空/被合并的元素存入临时数组*/
			TmpA[Tmp++] = A[R++];
		}
	}
	/* 如果左边数组还有剩余元素,那么直接复制左边剩下的,这里的两个小while只会执行其中一个. */ 
	while(L <= LeftEnd){
		TmpA[Tmp++] = A[L++];
	}
	/* 如果右边数组还有剩余元素,那么直接复制右边剩下的,这里的两个小while只会执行其中一个. */ 
	while(R <= RightEnd){
		TmpA[Tmp++] = A[R++];
	}
	/*
	把TmpA中的结果导回到A中,从右向左导回,而不是从左向右导回.
	可以理解成NumElements与RightEnd相等,在初始化时已经处理过了.
	*/
	for(i = 0; i < NumElements; i++, RightEnd--){
		A[RightEnd] = TmpA[RightEnd];
	}

}

9.4.2 递归算法 (分而治之)(稳定性-O(NLogN))

/*
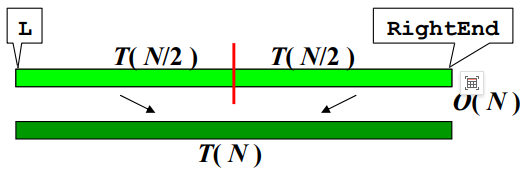
递归算法(需要占用系统的堆栈,有很多额外的操作,都让递归比较慢)-分而治之.
时间复杂度,递归去解决:
左半边用的时间T(N/2)+右半边用的时间T(N/2)+归并的时间复杂度O(N)数量级
T(N) = T(N/2) + T(N/2) + O(N) ->推出-> T(N) = O(NLogN)
没有最好/最坏/平均时间复杂度,任何情况下都是O(NLogN).
*/
/*
ElementType A[]原始待排的元素数组。
ElementType TmpA[]临时数组。
L指当前待排的序列最左边的位置。
RightEnd指当前待排的序列最右边的位置。
Center记录中间的位置。
*/
void MSort(ElementType A[], ElementType TmpA[], int L, int RightEnd){
	int Center;
	/*如果数组中只剩一个元素了(L = RightEnd),那么直接返回.*/
	if(L < RightEnd){
		/*Center记录中间的位置*/
		Center = (L + RightEnd) / 2;
		/*左半边递归排序*/
		MSort(A, TmpA, L, Center);
		/*右半边递归排序*/
		MSort(A, TmpA, Center + 1, RightEnd);
		/*
		子列合并
		L:左边的起始点。
		Center + 1:右边的起始点。
		RightEnd:右边的终点。
		*/
		Merge(A, TmpA, L, Center + 1, RightEnd);
	}
}

统一函数接口(公共抽取)

/*
统一函数接口-结合图形:始终都在数组的某一段反复的做声明临时数组、排序并合并到原数组的操作.
只传:
ElementType A[]原始待排的元素数组
TmpA临时数组
*/
void Merge_sort(ElementType A[], int N){

	ElementType *TmpA;
	/*临时数组TmpA的声明,malloc函数只调用了一次.*/
	TmpA = malloc(N * sizeof(ElementType));
	if(TmpA != null){
		/*
		ElementType A[]原始待排的元素数组.
		TmpA临时数组,声明在这里,而不是其他函数中.
		0待排序列左边的位置.
		N - 1:待排序列右边的位置.
		*/
		MSort(A, TmpA, 0, N - 1);
		/*一定要记得释放临时数组!,free函数也只声明了一次.*/
		free(TmpA);
	}else{
		Error("空间不足");
	}

}

在Merge中声明临时数组的问题

源码:递归算法实现归并排序

/*
有序子列的归并-根据案例图看源码-从TMPA导回A
所有的内容归并到A中,A中元素的结果是有序的.
如果两个子列一共有N个元素，那么这一趟归并(每个元素被扫描了一遍,每个元素被存进来一次)的时间复杂度T(N)=O(N).
*/
/* 
ElementType A[]原始待排序列
ElementType TmpA[]临时数组,存储归并以后的结果.
L = 要合并的左边起始位置
R = 要合并的右边起始位置
RightEnd = 右边终点位置 
*/
void Merge(ElementType A[], ElementType TmpA[], int L, int R, int RightEnd){

	/* 左边终点位置。假设左右两列挨着 */
	LeftEnd = R - 1;
	/* 存放结果的数组的初始位置 */
	Tmp = L;
	/*归并完成后中间元素的总个数*/
	NumElements = RightEnd - L + 1;
	/*
	L小于等于左边终点R小于等于右边终点
	*/
	while(L <= LeftEnd && R <= RightEnd){
		if(A[L] < A[R]){
			TmpA[Tmp++] = A[L++];
		}else{
			/*不为空/被合并的元素存入临时数组*/
			TmpA[Tmp++] = A[R++];
		}
	}
	/* 如果左边数组还有剩余元素,那么直接复制左边剩下的,这里的两个小while只会执行其中一个. */ 
	while(L <= LeftEnd){
		TmpA[Tmp++] = A[L++];
	}
	/* 如果右边数组还有剩余元素,那么直接复制右边剩下的,这里的两个小while只会执行其中一个. */ 
	while(R <= RightEnd){
		TmpA[Tmp++] = A[R++];
	}
	/*
	把TmpA中的结果导回到A中,从右向左导回,而不是从左向右导回.
	可以理解成NumElements与RightEnd相等,在初始化时已经处理过了.
	*/
	for(i = 0; i < NumElements; i++, RightEnd--){
		A[RightEnd] = TmpA[RightEnd];
	}

}



/*
递归算法-分而治之
时间复杂度,递归去解决:
左半边用的时间T(N/2)+右半边用的时间T(N/2)+归并的时间复杂度O(N)数量级
T(N) = T(N/2) + T(N/2) + O(N) ->推出-> T(N) = O(NLogN)
没有最好/最坏/平均时间复杂度,任何情况下都是O(NLogN).
*/
/*
ElementType A[]原始待排的元素数组.
ElementType TmpA[]临时数组,存储归并以后的结果.
L指当前待排的序列最左边的位置.
RightEnd指当前待排的序列最右边的位置.
Center记录中间的位置.
*/
void MSort(ElementType A[], ElementType TmpA[], int L, int RightEnd){
	int Center;
	/*如果数组中只剩一个元素了(L = RightEnd),那么直接返回.*/
	if(L < RightEnd){
		/*Center记录中间的位置*/
		Center = (L + RightEnd) / 2;
		/*左半边递归排序*/
		MSort(A, TmpA, L, Center);
		/*右半边递归排序*/
		MSort(A, TmpA, Center + 1, RightEnd);
		/*
		子列合并
		L:左边的起始点。
		Center + 1:右边的起始点。
		RightEnd:右边的终点。
		*/
		Merge(A, TmpA, L, Center + 1, RightEnd);
	}
}


/*
统一函数接口-结合图形:始终都在数组的某一段反复的做声明临时数组、排序并合并到原数组的操作.
只传:
ElementType A[]原始待排的元素数组
TmpA临时数组
*/
void Merge_sort(ElementType A[], int N){

	ElementType *TmpA;
	/*临时数组TmpA的声明,malloc函数只调用了一次.*/
	TmpA = malloc(N * sizeof(ElementType));
	if(TmpA != null){
		/*
		ElementType A[]原始待排的元素数组.
		TmpA临时数组,声明在这里,而不是其他函数中.
		0待排序列左边的位置.
		N - 1:待排序列右边的位置.
		*/
		MSort(A, TmpA, 0, N - 1);
		/*一定要记得释放临时数组!,free函数也只声明了一次.*/
		free(TmpA);
	}else{
		Error("空间不足");
	}

}

9.4.3 非递归算法 (稳定性-O(N))

非递归算法的基本思路:假设在一开始一共有N个有序的子序列，每个子序列中都只含有一个元素，下一步要做的是，把相邻的两个有序的子序列做一次归并。

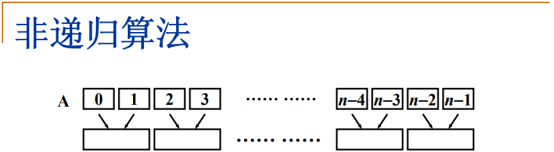
于是形成若干个有序的子序列，每个子序列的长度变成2，每个子序列中包含2个元素，这2个元素之间是有序的。

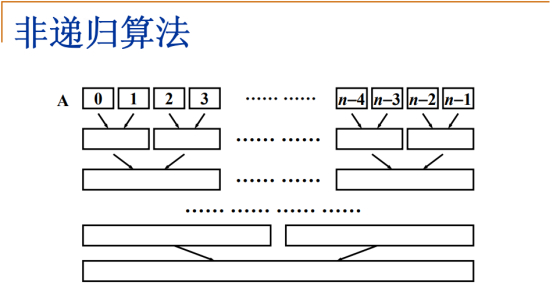
继续归并，长度变成4，最后得到一个完整的有序的序列。

额外空间:如果照着这个图来理解的话，这个额外的空间复杂度有些恐怖，层数为每次2，一直N为止，深度是LogN，如果在每一层开一个新的临时数组去存这个中间结果的话，额外的空间复杂度就变得十分庞大可怕了。

可以做到最小的额外空间复杂度是:O(N)。

实际上不用每次都开一个临时数组，用一个就够了，所以整个的执行过程，核心步骤就是一趟归并。

源码:非递归算法实现归并排序

/*
有序子列的归并-根据案例图看源码-不从TMPA导回A
所有的内容归并到TMPA中,TMPA中元素的结果是有序的.
如果两个子列一共有N个元素，那么这一趟归并(每个元素被扫描了一遍,每个元素被存进来一次)的时间复杂度T(N)=O(N).
*/
/* 
ElementType A[]原始待排序列
ElementType TmpA[]临时数组,存储归并以后的结果.
L = 要合并的左边起始位置
R = 要合并的右边起始位置
RightEnd = 右边终点位置 
*/
void Merge1(ElementType A[], ElementType TmpA[], int L, int R, int RightEnd){

	/* 左边终点位置。假设左右两列挨着 */
	LeftEnd = R - 1;
	/* 存放结果的数组的初始位置 */
	Tmp = L;
	/*归并完成后中间元素的总个数*/
	NumElements = RightEnd - L + 1;
	/*
	L小于等于左边终点R小于等于右边终点
	*/
	while(L <= LeftEnd && R <= RightEnd){
		if(A[L] < A[R]){
			TmpA[Tmp++] = A[L++];
		}else{
			/*不为空/被合并的元素存入临时数组*/
			TmpA[Tmp++] = A[R++];
		}
	}
	/* 如果左边数组还有剩余元素,那么直接复制左边剩下的,这里的两个小while只会执行其中一个. */ 
	while(L <= LeftEnd){
		TmpA[Tmp++] = A[L++];
	}
	/* 如果右边数组还有剩余元素,那么直接复制右边剩下的,这里的两个小while只会执行其中一个. */ 
	while(R <= RightEnd){
		TmpA[Tmp++] = A[R++];
	}
	/*
	把TmpA中的结果导回到A中,从右向左导回,而不是从左向右导回.
	可以理解成NumElements与RightEnd相等,在初始化时已经处理过了.
	*/
	/*这里无导回A的操作*/
	/*for(i = 0; i < NumElements; i++, RightEnd--){
		A[RightEnd] = TmpA[RightEnd];
	}*/

}


/*
非递归算法-这里完成了一趟归并
如果要归并的子序列是偶数个,那么正好是成对的.
如果要归并的子序列是奇数个,那么最后就会多出来一个.
*/
/* 
N整个待排序列的长度
length = 当前有序子列的长度 
ElementType A[]原始待排的元素数组.
ElementType TmpA[]临时数组,存储归并以后的结果.
*/
void Merge_pass(ElementType A[], ElementType TmpA[], int N, int length){

	/*
	执行过程:从左到右.
	i:表示最左边的位置.
	i + 2 * length - 1:下一段的终止位置.
	i+length:跳过这么长一段,下一段的初始位置.
	i += 2 * length:每次循环跳过2段位置.
	N - 2 * length:结束条件,并且保证序列成对存在.
	*/
	for(i = 0; i <= N - 2 * length; i += 2 * length){
		/*把A中元素归并到TmpA*/
		Merge1(A, TmpA, i, i + length, i + 2 * length - 1);
	}
	/* 
	归并最后2个子列 
	归并到最后的两段子序列长度可能不同,.
	*/
	if(i + length < N){
		/*最后一个子列的结尾无论如何都是N - 1,把最后两个子列合并一下.*/
		Merge1(A, TmpA, i, i + length, N - 1);
	}
	else{
		/*i + length之后跳到N外面去了,意味着最后只剩1个子列.*/
		for(j = i; j < N; j++){
			/*把剩下的A直接导入TMPA*/
			TmpA[j] = A[j];
		}
	}

}


/*
统一函数接口-结合图形:始终都在数组的某一段反复的做声明临时数组、排序并合并到原数组的操作.
只传:
ElementType A[]原始待排的元素数组
TmpA临时数组,跟原始数组等长
*/
/*
非常好的特性:稳定.
时间复杂度:平均复杂度和最坏时间复杂度都是NLogN.
最大的缺点:需要额外空间TMPA,需要在数组与数组之间复制和导回此元素.
此归并排序在外排序特别有用.
如果所有的元素都可以在内存中完成,那么没人会有内排序.
ElementType A[]原始待排的元素数组.
N整个待排序列的长度
*/
void Merge_sort(ElementType A[], int N){
	/*初始化子序列长度*/
	int length = 1;
	ElementType *TmpA;
	TmpA = malloc(N * sizeof(ElementType));
	if(TmpA != NULL){
		/*
		length当前子序列的长度
		每次循环做两次Merge_pass,保证最终的结果都在A中.
		*/
		while(length < N){
			/*把A导入TMPA,length=1*/
			Merge_pass(A, TmpA, N, length);
			/*length=2*/
			length *= 2;
			/*把TMPA导回A*/
			Merge_pass(TmpA, A, N, length);
			/*
			length=4
			如果执行到这步length=N,已经完全有序了,那也没关系.
			*/
			length *= 2;
		}
		free(TmpA);
	}else{
		Error("空间不足");
	}

}