10.1.1 算法概述

快速排序是现实应用中最快的一种排序算法。

但是，没有任何一种排序算法是在任何情况下都是最好的。

我们总是可以构造出最快情况下排序算法的表现。

对于大规模的随机数据，快速排序的表现，还是相当出色的，但前提是快速排序中所有的小细节都实现的十分到位。

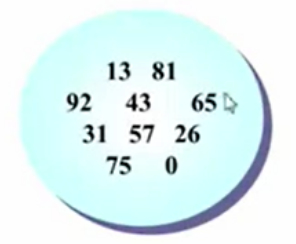
快速排序第一步:在这堆整数中随便挑一个整数作为主元。

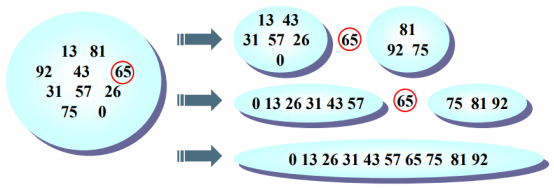
这里选择65作为中枢枢纽。

数字集合被分为两大块，左边的数字都小于65，右边的都大于65。

递归的去治理左边，递归的去治理右边。

把这三块数据最终都放到一个数组中，排序合并，就完成了最后的快速排序。

分而治之(分别递归左右两边-O(NLogN))

(1)选主元。

(2)根据主元划分子集，递归治理。

(3)快速排序、合并。

时间复杂度:中分的选择决定了快速排序算法好坏，当每一次选的主元位于数组的中间，把数组正好一分为二时，也就是把问题可以等分，那么，此时的快速排序算法的效率是最好的，

T(N) = O(NLogN)。

10.1.2 选主元 (Median3算法:三数中值法)

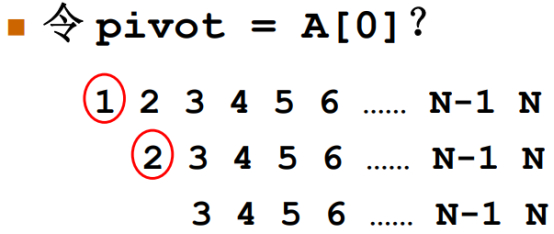
如果主元选择A的第一个元素A[0]，非常不合适的做法。

一开始是有序的。

第一步:第一行数字，选择A[0]作为主元之后，必须要把剩余的元素全部扫描一遍，发现这个主元是最小的。在子集划分时，发现主元的左边是空集，没数据，右边包含了N-1个元素，然后需要对这N-1个元素递归的处理，先递归处理第一层，后续重复此步骤，选择主元，又是选择的最左边的A[0]元素，重复此步骤。

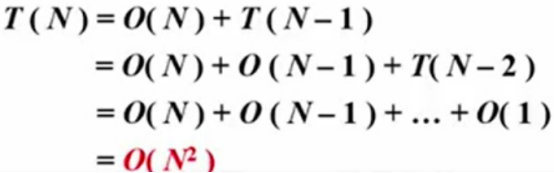
解决整个问题的时间复杂度，等于选择了主元，扫描一遍主体，这是O(N)的时间复杂度。

完成子集划分以后，剩下的东西包含着N-1个元素，然后递归的去处理这N-1个元素，花费了N-1的时间去继续做子集划分，递归的去解决N-2个元素，重复此步骤，一直到最后只剩下一个元素返回。

整个时间复杂度的和=O(N^2)。

此时间复杂度在所有的排序算法中是相当差的，编写递归程序，什么都没做，因为一开始序列就是有序的，并且还花费了O(N^2)，所以主元肯定不能按上述情况选择A[0]。

/*
选择主元
题目是选3个元素的中位数,还有选5个数,更复杂的7个数。
最小的一定放在最左边
*/
/*
ElementType A[]当前数组, 
int Left头, 
int Right尾
*/
ElementType Median3(ElementType A[], int Left, int Right){

	/* A[ Left ] <= A[ Center ] <= A[ Right ] */
	int Center = (Left + Right) / 2;
	/*
	最小的一定放在最左边,最大的一定在最右边.
	*/
	if(A[Left] > A[Center]){
		Swap(&A[Left], &A[Center]);
	}
	if(A[Left] > A[Right]){
		Swap(&A[Left], &A[Right]);
	}
	if(A[Center] > A[Right]){
		Swap(&A[Center], &A[Right]);
	}
	/* 
	将pivot藏到右边,Right - 1位置而不是Right位置,为了后续操作方便这么放置.
	因为right肯定比center大在右边,left在左边.
	当考虑子集划分的时候,根本不用考虑左右两个元素.
	*/
	Swap(&A[Center], &A[Right - 1]);
	/* 后续只需要考虑 A[ Left+1 ] … A[ Right–2 ] */
	/* 返回 pivot主元 */
	return A[Right - 1];

}

10.1.3 子集划分

调用上述Median3算法后，8和6两边的元素就不考虑了，6是选择的主元放在最右边的位置，要找元素6最终放置的位置。

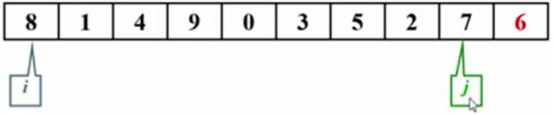
定制左右两边的指针i和j，记录它们的下标，比较和主元的大小。

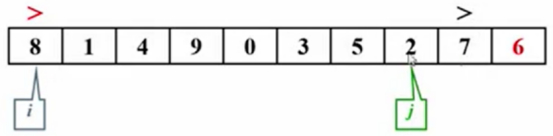
主元6左边的元素(i)都要小于6。

主元6右边的元素(j)都要大于6。

8>6红色警告，i不动。

7<6标记黑色，j移动一位指针。

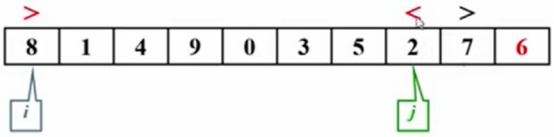
当j移动后，发现2<6，红色警告。

当发现两边都有不对的元素之后，把8和2交换一下，继续下一轮的比较。

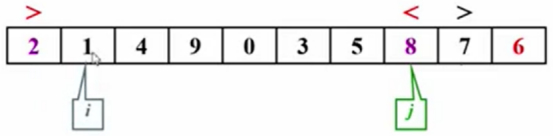
移动i指针，同时继续比较，1<6，黑色标记，重复上述比较步骤。

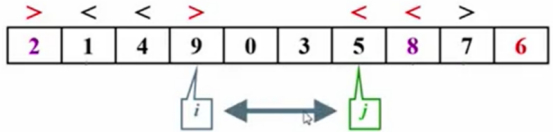
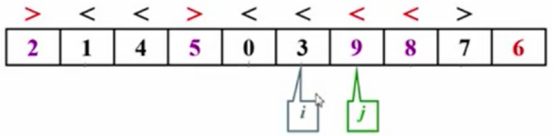
到这应该停住了，但是机器并不知道，会继续往前走，继续移动i的指针。

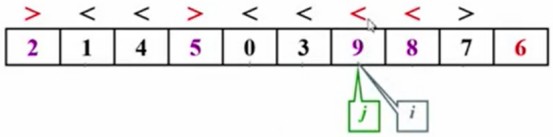
移动i的指针发现，9<6，红色标记，停止。

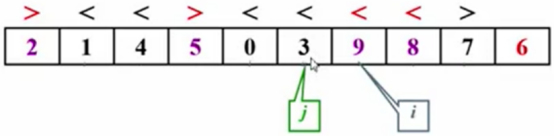
继续移动j的指针，3<6，并不符合j<主元6的逻辑 ，那么要停止后结束。

发现i<j，那么子集划分就要结束，那么主元6的位置就是i这个位置。

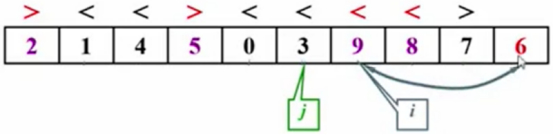
把A[i]与主元做交换，把主元放在应该放的位置。

快速排序为什么快

主元被选中之后，在子集划分完成之后，它被一次性的放在了正确的位置，以后再也不会移动。

不像插入排序，插入排序每一次做了元素交换以后，元素所持的位置只是临时的，当下一张扑克牌进来的时候，这些牌的位置全部都要往后错，所以一张牌可能在插入排序的过程中，被移动了很多次。

元素正好等于主元pivot怎么办

一种选择:停下来交换。

非常极端情况:这个序列中的所有元素都相等，比如1，首先调用median3，比头尾中间发现都不用动，于是把中间的median放到了右边，指针ij都跟主元相等，ij做交换，于是i++，j--，反复做了很多次没有用的交换，最后ij会停留在比较中间的位置。

这样做的好处，每一次递归，原始序列都被基本上等分成两个等长的序列，也就是N/2的序列，这样往下递归的时间复杂度为NLogN。

另一种选择:不理它，继续移动指针。

从左边指针i开始移动，碰到指针i指向的元素等于主元，那么不理主元，一直移动到最右边指针j的位置，那么指针j根本就没机会移动。

好处:避免很多没必要的交换。

坏处:每一次子集的划分，基本上主元都被放在某一个端点，最坏的时间复杂度O(N^2)。

小规模的数据处理(简单排序而非递归)

递归会占用额外的系统堆栈空间，有很多的进栈、进栈、进栈、、和POP、POP、POP。。

大规模数据再用递归，减少更多的进栈、POP操作。

阈值Cutoff(英ˈkʌtɒf,美ˈkʌtˌɔːf)当递归数据规模小于此阈值时，就不递归了，直接使用插入排序即可，不同的阈值对程序的效率有不同的影响。

10.1.4源码:算法实现 (统一接口模板)

#include<stdio.h>
/*
排序-快速排序-自己实现
*/
int main(void){
	return 0;
}
/*
选择主元
题目是选3个元素的中位数,还有选5个数,更复杂的7个数。
最小的一定放在最左边
*/
/*
ElementType A[]当前数组, 
int Left头, 
int Right尾
*/
ElementType Median3(ElementType A[], int Left, int Right){

	/* A[ Left ] <= A[ Center ] <= A[ Right ] */
	int Center = (Left + Right) / 2;
	/*
	最小的一定放在最左边,最大的一定在最右边.
	*/
	if(A[Left] > A[Center]){
		Swap(&A[Left], &A[Center]);
	}
	if(A[Left] > A[Right]){
		Swap(&A[Left], &A[Right]);
	}
	if(A[Center] > A[Right]){
		Swap(&A[Center], &A[Right]);
	}
	/* 
	将pivot藏到右边,Right - 1位置而不是Right位置,为了后续操作方便这么放置.
	因为right肯定比center大在右边,left在左边.
	当考虑子集划分的时候,根本不用考虑左右两个元素.
	*/
	Swap(&A[Center], &A[Right - 1]);
	/* 后续只需要考虑 A[ Left+1 ] … A[ Right–2 ] */
	/* 返回 pivot主元 */
	return A[Right - 1];

}

/*快速排序统一函数接口*/
void Quicksort(ElementType A[], int N){
	/*
	A待排原始数组,0起始位置,N-1终止位置.
	这里从最大数组开始递归解决快速排序问题.
	*/
	Quicksort(A, 0, N - 1);
}
/*快速排序递归函数接口*/
void Quicksort(ElementType A[], int Left, int Right){
	if(Cuttof <= Right - Left){
		/*
		调用Median3获取主元,也对原来数组的Left和Right做了修改.
		left保存三个元素中的最小值.
		right保存三个元素中的最大值.
		真正的主元Pivot在right-1的位置.
		*/
		Pivot = Median3(A, Left, Right);
		/*左端下标,也可以写成left-1*/
		i = Left;
		/*右端下标,也可以写成right-2*/
		j = Right - 1;
		/*将序列中比基准小的移到基准左边，大的移到右边*/
		for( ; ; ){
			/*从左向右移动,大于主元那么红色警告停下来,移动指针j*/
			while(A[++i] < Pivot){
			}
			/*从右向左移动,小于主元那么红色警告停下来,移动指针i*/
			while(A[--j] > Pivot){
			}
			/*上述循环挺停掉,如果i<j这个顺序,那么互换ij二者元素位置,否则自己划分是结束的.*/
			if(i < j){
				Swap(&A[i], &A[j]);
			}else{
				break;
			}
		}
		/*子集划分后,要把放在right-1的主元pivot放在A[i]这个位置.*/
		Swap(&A[i], &A[Right - 1]);
		/*递归排序主元左边的元素*/
		Quicksort(A, Left, i - 1);
		/*递归排序主元右边的元素*/
		Quicksort(A, i + 1, Right);
	}else{
		/*
		小于阈值直接跳出,元素太少,直接用简单排序-插入排序.
		A + Left:开始位置.
		Right - Left + 1:当前待排序列元素的总个数.
		*/
		InsertionSort(A + Left, Right - Left + 1);
	}
}

源码-算法实现(直接调用库函数)

#include<stdio.h>
/*
排序-快速排序-直接调用库函数
*/
int main(void){
	return 0;
}

/*---------------简单整数排序--------------------*/
int compare(const void *a, const void *b){
	/* 比较两整数。非降序排列 */
	return (*(int*)a - *(int*)b);
}
/* 调用接口 */ 
qsort(A, N, sizeof(int), compare);
/*--------------- 一般情况下，对结构体Node中的某键值key排序 ---------------*/
struct Node{
	int key1, key2;
}A[MAXN];

/* 比较两种键值:如果key1不相等,按key1非升序排列;如果key1相等,则按key2非降序排列. */
int compare2keys(const void *a, const void *b){
	int k;
	/* 如果key1不相等,按key1非升序排列 */
	if((((const struct Node*)a)->key1) < (((const struct Node *)b)->key1)){
		key = 1;
	}else if((((const struct Node*)a)->key1) > (((const struct Node *)b)->key1)){
		key = -1;
	}
	/* 如果key1相等,则按key2非降序排列. */
	else{
		if((((const struct Node*)a)->key2) < (((const struct Node*)b)->key2)){
			key = -1;
		}else{
			key = 1;
		}
	}
	return k;
}
/* 调用接口 */
qsort(A, N, sizeof(struct Node), compare2keys);