10.2.1表排序算法 (先)

概述

什么情况用到表排序？

待排元素不是一个个简单的整数，而是一个个庞大的结构，比如一本书、结构体，其中包含了非常多的元素，而且非常复杂，而移动这本书的时间是不能忽略不计的。

再比如当排序算法涉及频繁交换元素时，需要移动元素，当移动的元素比如是一部2BG的电影，不停的移来移去是一件很恐怖的事情。

那么表排序，是在排序过程中，实际上是不需要移动这些原始数据的，移动的只是指向它们位置的指针，只移动指针的这种排序方法叫做间接排序方法。

间接排序

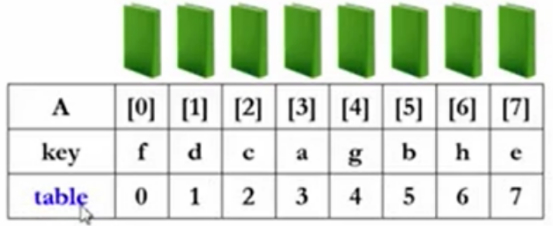
待排序列A，

序列A中的每个元素都有一个关键字key，

定义table给每个元素定义一个指针。

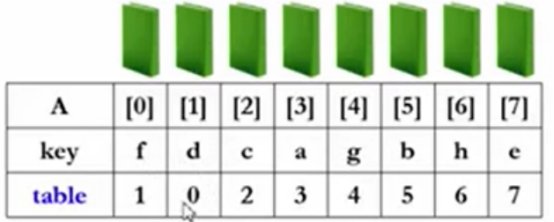
假设第一本书已经存在，比较第一本书A[0]和第二本书A[1]的大小，发现d<f，交换这两个指针，小的往前放，所以位置0放的是A[1]，位置1放的是A[0]。这就是第1趟的内容。得下述内容102。

(注意:新插入的值肯定在A[0]的右边，通过A[0]找f，如果比f小，那么就交换，否则不交换，要注意的是，指针位置虽然变化了，但是指针指向的原值是不变的，比如table[0]永远指向A[0]，A[0]永远指向值f。)

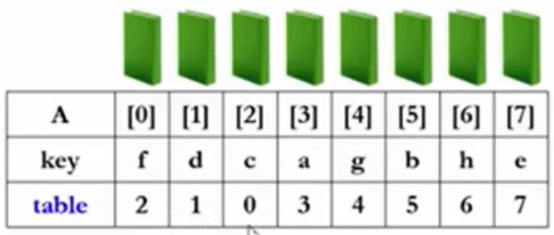
下一本书进来的是c，跟A[0]的值f比较，发现c<f，0和2先交换，指针顺序变成120，于是指针2对应的c(通过指针找KEY值)再跟A[1]的值d比较，那么指针1和2再变位置，变成210。最后，10都要往后错一位，2在第一位。这就是第2趟的内容。得下述内容210。

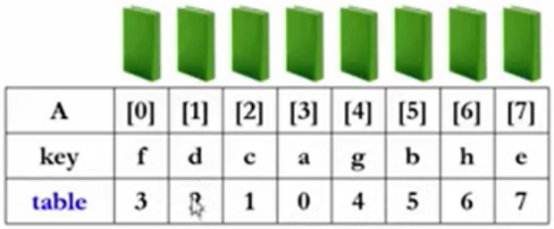
下一本书进来的是a，先和A[0]的值f比较，得到2130，再分别与前面的12分别比较做指针交换。这就是第3趟的内容。得下述内容3210。

下一本书进来的是g，发现g>A[0]/f，所以不用交换。

下一本书进来的是b，重复前面交换步骤。这就是第5趟的内容。得下述内容352104。

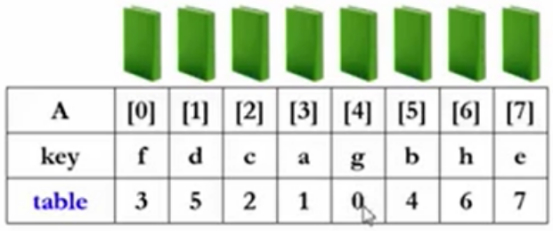
下一本书进来的是h，发现h>A[4]/g，所以不用交换。

下一本书进来的是e，重复前面交换步骤，e<table[6]/h，6和7交换位置，得到35210476。逐渐和下标40做比较，这就是第6趟的内容。得下述内容35217046。

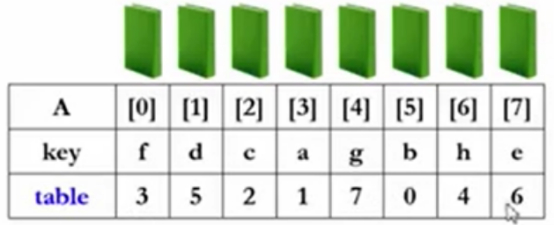
顺序输出

直接按照下标顺序输出值即可，没必要动任何一个元素的位置。

10.2.2 物理排序 (后)(O(mN))

环的构成

在表排序完成后，需要把所有的元素做物理排序，也就是非得把所有的书在物理上按照顺序给排出来。

那么可以在线性的时间复杂度内把物理排序做出来，利用了下述非常重要的原理。

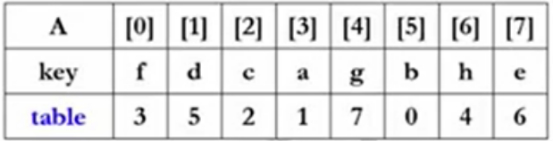
回到刚才表排序完成之后的例子结果中，table的值从0-7，对应8个数字的排列，这个排列一定由若干个独立的环组成。

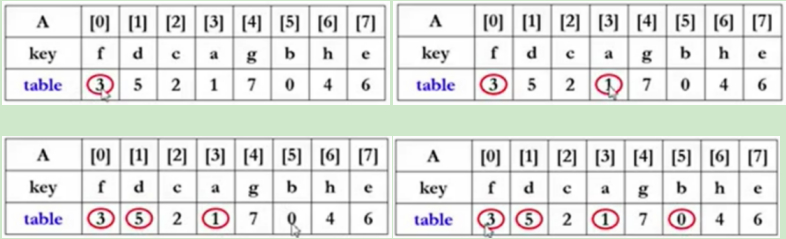
先从table[0]开始，跳到table[3]，跳到table[1]，跳到table[5]，跳到table[0]原始点，这4个数字构成一个环。下个环就是继续对没圈起来的数。

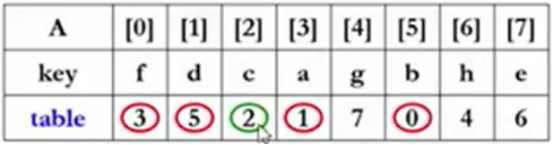
发现table[2]就是它自己，构成一个环。

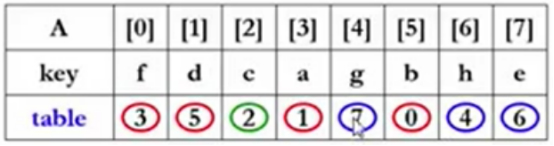
先从table[4]开始，跳到table[7]，跳到table[6]，跳到table[4]原始点，这3个数字构成一个环。

====上述三个环是相互独立的，意味着在调整时，可以按照一个一个环的方法来调整这些书的位置。

处理环中元素的错位

比如对红色环中的四本书处理，错位如何处理？

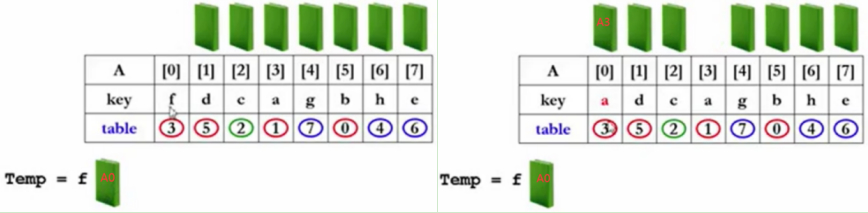
先把A[0]第一本书拿下来，存在临时位置，书架A[0]位置就空出来了，此时应该放A[3]这本书，A[0]的key从f变成a，那么A[3]位置就空出来了。

(A[0]下放temp，A[0]空出，A[3]挪到A[0]，A[3]空出，A[0]的KEY:f变a。注意以下步骤TEMP为A[0]的值f不变。被填充的KEY的值改变。)

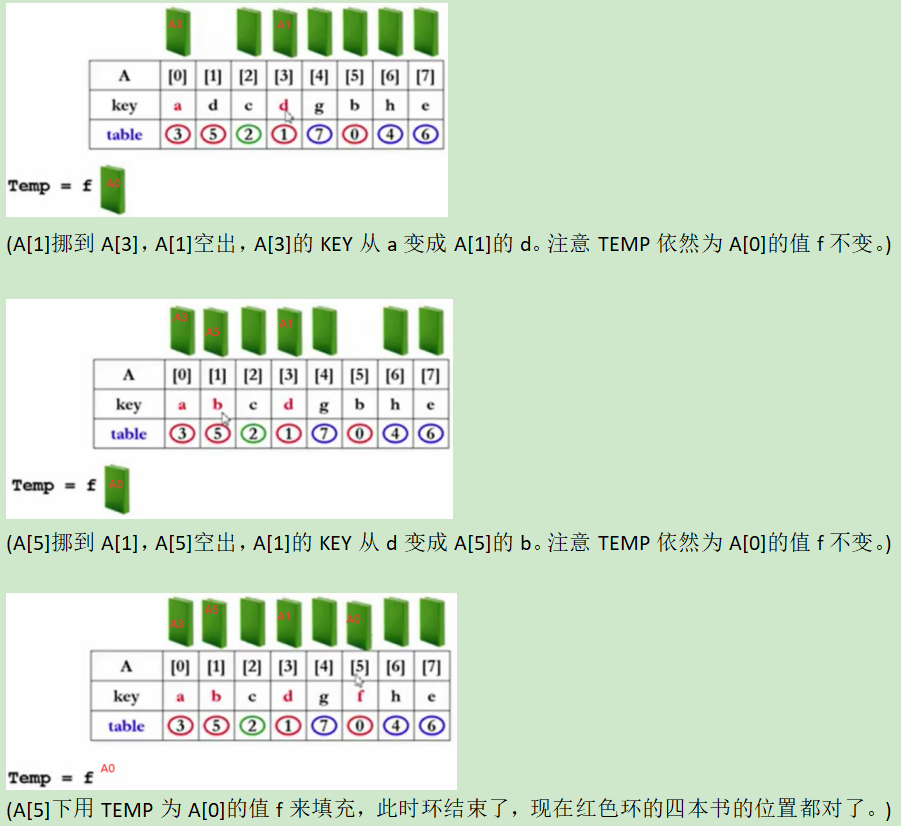
判断环的结束

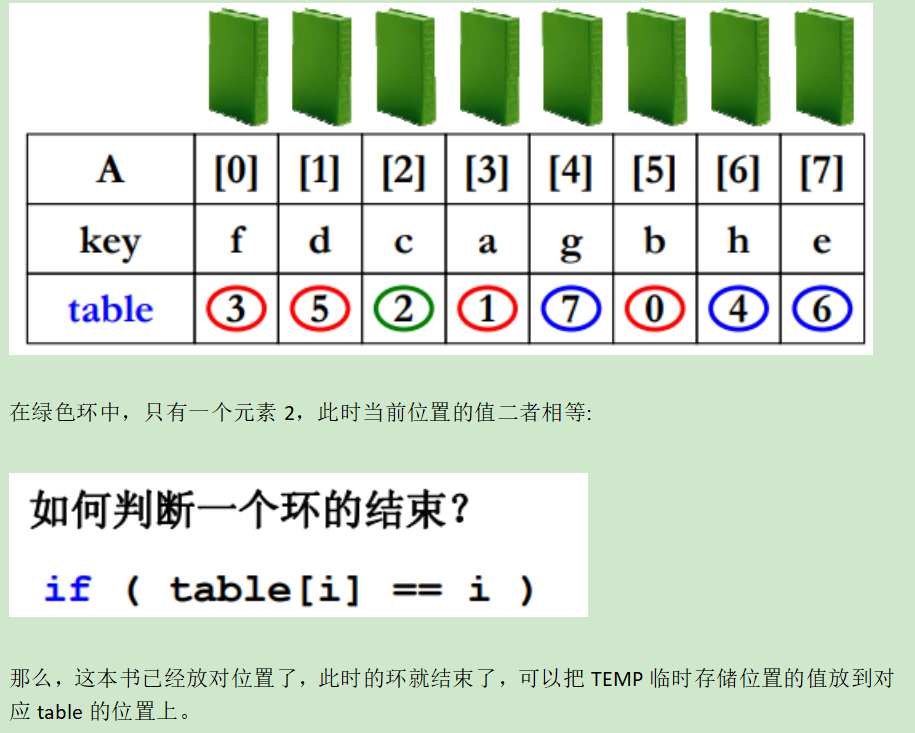
复杂度分析

物理排序过程的最好情况:初始就是有序的，什么都不用再做了。

物理排序过程的最坏情况:如果所有的环只包含两个元素，整体就会有N/2个环，两个元素直接做swap交换，比如把一本书放到临时TEMP，另一本书再放过去，之后临时TEMP的书再放回去，对于每两本书，都需要三步操作。即每个环包含2个元素，交换2个元素需要走3步，需要3N/2次的元素移动。

当一次元素移动的时间不可忽略，是一种非常糟糕的情况，那么可以写成O(N)的时间复杂度，那么每个元素的移动时间都不可忽略的话，那么常数m就是一个比较大的数值不可忽略，所以整体的时间复杂度是O(mN)。