11.4 散列表的性能分析 (成功/插入ASLs和不成功ASLu)

概要(装填因子-空间换时间)

在散列中的元素，平均要找多少次。

不在散列中的元素，平均要找多少次。

散列函数不均匀，那么冲突会多，性能会差，装的元素越多，冲突就会越大，装载因子就越大，这是理论上的结果，实际值跟理论值还是有差异的。

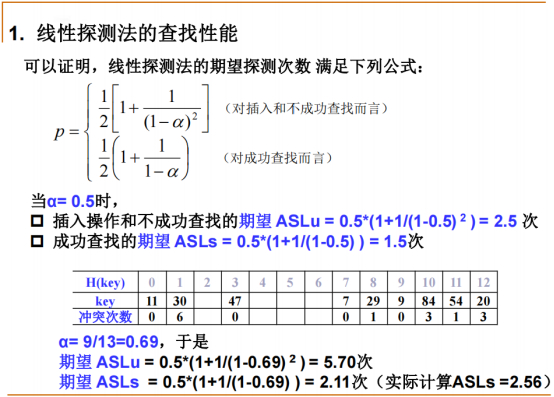
线性探测法(期望与实际)

平方探测法与双散列探测法(期望与实际)

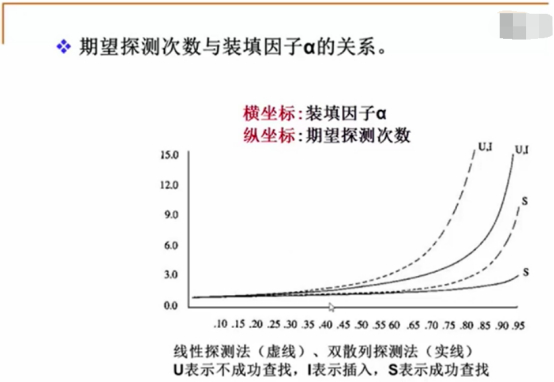
在装载因子不到一半的时候，冲突次数在3次之内，当装载因子逐步变大的时候，冲突是一下子升的很快，特别是线性探测。

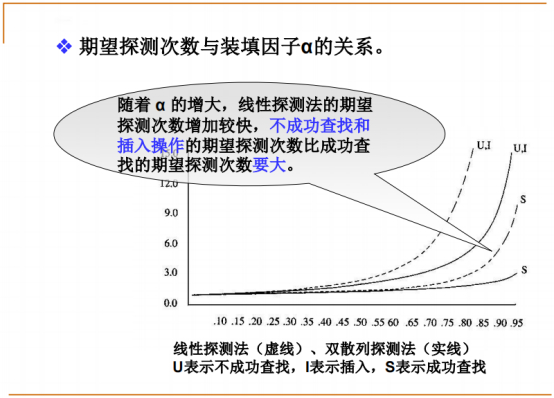
双散列探测成功查找的次数，随着装载因子的提升，成功的增长比较慢，失败的增长很快。

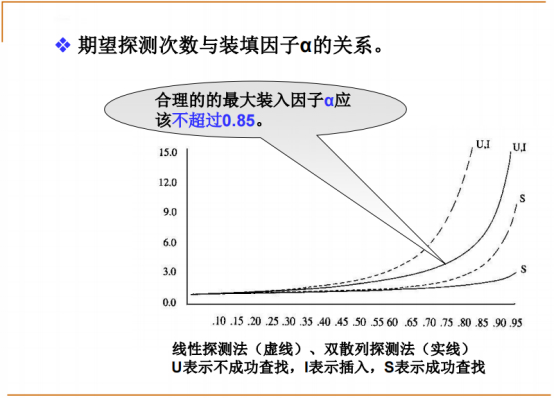
装载因子超过0.85是不能容忍的。

分离链接法(期望与实际)

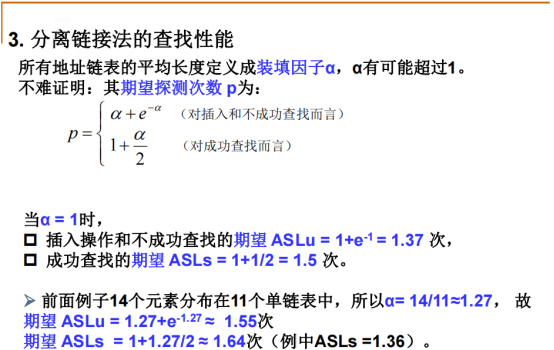
因为元素是放在链表中的，所以元素的个数可能会超过散列表这个数组的大小。

在这个例子中，有9个元素在链表头上，所以查找9次就够了，有5个元素在链表的第二个位置，要查找2次。

散列/哈希查找特点(O(1)-空间换时间-存储关键字随机)

(1)散列值的查找通过散列函数计算出位置，跟问题的规模无关(二叉树Log2N就有关了)，不发生冲突，一次查找成功，否则通过好的冲突处理方法降低冲突次数而达到个位数。

散列查找很多时候用于字符串的查找，用于字符串的管理，比如WEB搜索的关键字，需要一个字符去比较，通过哈希函数计算成数字再比较。

(2)装载因子小，散列表的占有率就小，那么冲突就少。

(3)如果是二叉树，那么比较适合顺序查找、范围查找、最大值最小值查找，没这些条件的话，那么散列方法也适合。

散列表解决方案(装填因子不能>0.85)

开放地址法(数组、聚集)

数组的效率比链表要高。

某位置被占用后，很容易在它的周围产生新的聚集。

分离链接法 /链地址法(顺序+链表-装填因子)

数组中的指针指向单向链表，发生冲突就会去链表中查找元素，冲突越多，链表越长，装载因子越大，浪费空间和时间，查找效率就降低。