题意理解与解法分析

N=4，下面是4条通话记录，一条通话记录两个号码。

把通话记录最多的号码和次数输出。

解法1-排序(N^2LogN)

最大的N=10^5，每条记录两个号码。

重复出现的号码肯定都排在一起的。

从头到尾去扫描有序数组，相同号码肯定是连续出现的，需要变量统计出现的次数。

此解法并不好，通话记录并不是一成不变的，每时每刻都有通话，每来一条通话都要找一次的话，都要做一个NLogN的排序，如果要做N次，那么算法复杂度就是N^2LogN。

解法2-直接映射(N^2LogN)

目前为止电话号码的第一位都是1，电话号码11位，一条通话记录是两个电话号码，所以

2*10^10足够了。

平时用到的整数是unsigned long长度是10位，但电话号码11位，用long long吗?

即使把每个整数都记成短整数，开辟此数组，也大约需要40GB的内存空间。

找号码多花了2*10^5倍的时间。

那么算法复杂度是N^2LogN。

虽然带了散列的概念，但是过分的简单粗暴。

解法3-分离链接法(O(N))

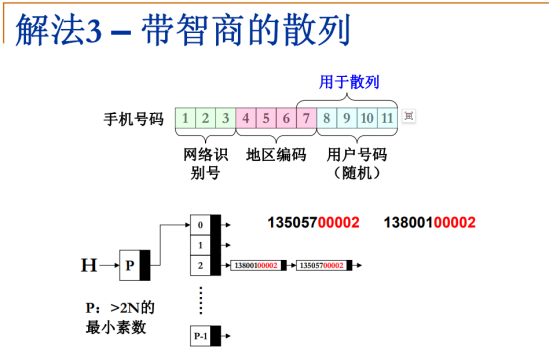
网络识别号不适合在散列函数中计算，因为种类太少。

地区编码同上。

用户号码是随机的，适合作为散列函数计算，但效果不太好，再取地区编码的最后一位和用户号码一起求散列计算。

散列头素数P存散列表的长度(散列表头结点的个数)，应该略大于2N(号码个数)的素数。

比如后五位第五位元素是2，那么插入数组下标2的位置中去，第一个元素直接插入链表，第二个元素后五位如果冲突，那么插入链表的表头，第三个元素如果重复出现，那么会先扫描这个链表，如果找到相同号码，则此号码计数器+1，否则，继续插入表头。当然希望是链表表长不太长，冲突不多，所以整体效率还是线性的，O(N)数量级。

源码

/*
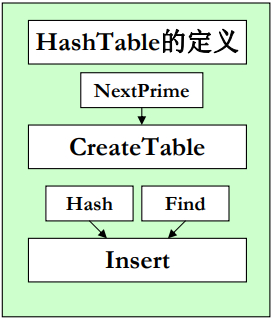
散列查找-分离链接法-电话号码
*/
#include<stdio.h>
#include<math.h>

/* 关键词字符串的最大长度 */
#define KEYLENGTH 11
/* 
关键词类型用字符串 
C语言字符串末尾的'\0'位置
*/
#define char ElementType[KEYLENGTH + 1];
/* 散列地址类型 */
typedef int Index;

typedef struct LNode *PtrToLNode;
struct LNode{
	ElementType Data;
	PtrToLNode Next;
	int Count;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;

typedef struct TblNode *HashTable;
/* 散列表结点定义 */
struct TblNode{
	/* 表的最大长度 */
	int TableSize;
	/* 指向链表头结点的数组 */
	List Heads;
};

int main(){

	int N, i;
	ElementType Key;

	HashTable H;

	scanf("%d", &N);

	/*创建一个散列表*/
	H = CreateTable(N * 2);
	/*每次读进来一对*/
	for(i = 0; i < N; i++){
		scanf("%s", Key); Insert(H, Key);
		scanf("%s", Key); Insert(H, Key);
	}
	/*
	扫描整个散列表:
	更新最大通话次数.
	更新最小号码+统计人数.
	*/
	ScanAndOutput(H);
	/*释放散列表的空间*/
	DestroyTable(H);

	return 0;
}

#define MAXTABLESIZE 1000000
/* 返回大于N且不超过MAXTABLESIZE的最小素数*/
int NextPrime(int N){
	/*从大于N的下一个奇数开始*/
	int i, p = (N % 2) ? (N + 2) : (N + 1);
	/*要返回大于给定的N,并且不超过指定的素数.*/
	while(p <= MAXTABLESIZE){
		for(i = (int)sqrt(p); i > 2; i--){
			if(!(p % i)){
				/* p不是素数*/
				break;
			}
			if(i == 2){
				/* for正常结束，说明p是素数*/
				break;
			}else{
				/* 否则试探下一个奇数*/
				p += 2;
			}
		}
	}
	return p;
}

/* 
除留余数法法散列函数
Key是整数:手机号码后五位已经截取出来并变成了整数
*/
int Hash(int Key, int P){
	return Key % P;
}

/*
创建一个散列表
生成一个比记录大小更大的素数
传进来的是用户指定的数组大小2N
*/
HashTable CreateTable(int TableSize){
	HashTable H;
	int i;
	H = (HashTable)malloc(sizeof(struct TblNode));
	H->TableSize = NextPrime(TableSize);
	H->Heads = (List)malloc(H->TableSize * sizeof(struct LNode));
	for(i = 0; i < H->TableSize; i++){
		H->Heads[i].Data[0] = '\0';
		H->Heads[i].Next = NULL;
		/*初始化变量头结点的计数器,好的习惯.*/
		H->Heads[i].Count = 0;
	}
	return H;
}

/*参数散列映射计算的字符个数*/
#define MAXD 5
Position Find(HashTable H, ElementType Key){
	Position P;
	Index Pos;
	/* 
	初始散列位置 
	Key指向电话号码的第一位
	KEYLENGTH电话号码一共11位长度
	MAXD字符个数5
	*/
	Pos = Hash(atoi(Key + KEYLENGTH - MAXD), H->TableSize);
	/* 从该链表的第1个结点开始 */
	P = H->Heads[Pos].Next;
	/* 当未到表尾，并且Key未找到时 */
	while(P && strcmp(P->Data, Key)){
		P = P->Next;
	}
	/* 此时P或者指向找到的结点，或者为NULL */
	return P;
}

bool insert(HashTable H, ElementType Key){
	Position P, NewCell;
	Index Pos;
	P = Find(H, Key);
	/* 关键词未找到，可以插入 */
	if(!P){
		NewCell = (Position)malloc(sizeof(struct LNode));
		strcpy(NewCell->Data, Key);
		NewCell->Count = 1;
		/* 
		初始散列位置 
		Key指向电话号码的第一位
		KEYLENGTH电话号码一共11位长度
		MAXD字符个数5
		*/
		Pos = Hash(atoi(Key + KEYLENGTH - MAXD),H->TableSize);
		/* 将NewCell插入为H->Heads[Pos]链表的第1个结点 */
		NewCell->Next = H->Heads[Pos].Next;
		H->Heads[Pos].Next = NewCell;
		return true;
	}else{
		/* 关键词已存在,打印而是计数器+1. */
		P->Count++;
		return false;
	}

}


void ScanAndOutput(HashTable H){
	int i, MaxCnt = PCnt = 0;
	ElementType MinPhone;
	List Ptr;
	MinPhone[0] = '\0';
	/* 扫描链表*/
	for(i = 0; i < H->TableSize; i++){
		Ptr = H->Heads[i].Next;
		while(Ptr){
			/* 更新最大通话次数*/
			if(Ptr->Count > MaxCnt){
				MaxCnt = Ptr->Count;
				strcpy(MinPhone, Ptr->Data);
				PCnt = 1;
			}else if(Ptr->Count == MaxCnt){
				PCnt++;
				if(strcmp(MinPhone, Ptr->Data) > 0)){
					/* 更新狂人的最小手机号码*/
					strcpy(MinPhone, Ptr->Data);
				}
			}
			Ptr = Ptr->Next;
		}
	}
	printf("%s %d", MinPhone, MaxCnt);
	if(PCnt > 1){
		printf("%d", PCnt);
	}
	printf("\n");
}


/*释放散列表的空间*/
void DestroyTable(HashTable H){

	int i;
	Position P, Tmp;
	/* 释放每个链表的结点 */
	for(i = 0; i < H->TableSize; i++){
		P = H->Heads[i].Next;
		while(P){
			Tmp = P->Next;
			free(P);
			P = Tmp;
		}
	}
	/* 释放头结点数组 */
	free(H->Heads);
	/* 释放散列表结点 */
	free(H);

}